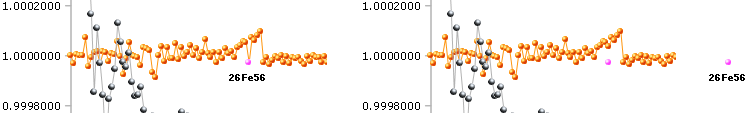TNEDa0 UNIVERSUMS
HISTORIA | a![]() production
2020IV25 | Efter sammanställningar från
1986-1991+ | Senast uppdaterade version: 2023-12-11 · Universums Historia
production
2020IV25 | Efter sammanställningar från
1986-1991+ | Senast uppdaterade version: 2023-12-11 · Universums Historia
innehåll
denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning alla webbsidor
Genombrotten
i TNED ¦
ironCORE ¦ FUSIONSELLIPSERNAS FULLSTÄNDIGA FÖRKLARING I TNED
INLEDANDE EXEMPEL
FUSIONSELLIPSERNAS KOPPLING TILL TUNGA
NUKLIDGRUPPEN KLARLAGD ¦ FusionsEllipsernaAVprincip
MICROSOFT
efter Bill Gates-eran (vi vet inte exakt, men åt det hållet) KLARAR
INTE AV DATORPROGRAMMERING I KONKRET MATEMATIK
Inledning: Story
TNED FRÅN BÖRJAN hur det hela började ..
ENHET UTAN DELAR
KOMPLEMENT TILL KÄRNFYSIKEN efter flera genombrott Apr2020
TNED FRÅN BÖRJAN ¦ noMASSorigin
ENHET UTAN DELAR är själva grundpremissen i hela Fysikboken. Annars går det inte: sammanhang utan luckor.
Massans upplösning i värme och ljus: (m→γ) noll restmassa. PRINCIPAL¦principle STRUCTURE OF MASS ¦ PASTOM.
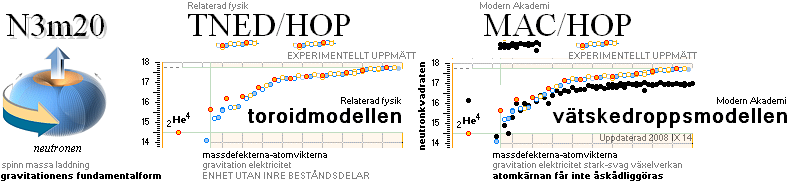
KÄRNFYSIKEN i Modern Akademi:
»Fristående vattendroppar ur en vattenmassas delning FINNS verksamma inuti
vattenmassan som FRISTÅENDE partiklar i rörelse»:
Atomkärnan INNEHÅLLER Neutroner och
Protoner: Mänsklighetens detaljerbart bevisligt allra mest PRIMITIVA
föreställning. Jämför Naturboken relaterad fysik:
KÄRNFYSIKEN i Relaterad Fysik: Atomkärnan är partikellös men Strukturen kan beskrivas EKVIVALENT utifrån dess observerbara fristående partikelfragment: np-strukturen.
Se även den kortare sammanställningen i GENOMBROTTEN I TNED.
TNEDbeginStory: Hur började den här Historien?
TNED FRÅN BÖRJAN
TOROID NUKLEÄRA ELEKTROMEKANISKA DYNAMIKEN TNEDbegin
StabDIFF ¦ PLANCKRINGEN
h = mcr neutronen ¦
Neutronkvadratens
kärnmatematik måste hanteras strängt med början från mD=0, neutronen, och uppåt
med hjälp av de givna fasta och fixa masstalens mD-värden. neutronkvadratens
egen specifika mönsterform.
På dessa vilar sedan hela nuklidkartans
bevisbarhet: härledningen till samtliga möjliga grundämnesatomer genom
exotermiska fusioner sådana som entydigt ger ut värme och ljus i
föreningarna; alltså sådana fusioner som inte kräver extra yttre moment för att
realiseras; med andra ord, endast sådana fusioner som realiseras då
atomkärnorna redan ligger innanför varandras nuklidbarriärer, och därmed kan
utföra spontana föreningar utan behov av yttre moment för att komma in i
föreningsläget.
I
en allra mest sammanfattande kort syntes:
Vad går hela den här framställningen
ut på?
SVAR:
Detaljerade bevis för korrekt natur- och fysikbeskrivande atom- och
kärnfysikalisk teori:
StabDIFF ¦ PLANCKRINGEN
h = mcr neutronen ¦
Den moderna
akademin (1800+) plågas förvisso svårt av bristen på inblick i naturdjupet. Det
är speciellt uppenbart i ljuset av det trängande behovet av MILJÖVÄNLIG ENERGI
som inte icke resulterar i naturmord. Mänskligheten tvingas följa i spåren
av förödelsen: förmågan att uppröras i blotta åsynen av en pågående
naturmisshandel (särskilt tydlig 2010+ i Sverige) har ingen som helst synbar
medial representation. Inte ett ord 2020. Inga uppslag. Inga diskussioner.
Ingen kritik. Och ingen hjälp ser heller ut att vara på ingående.
Modern akademi kontra relaterad
fysik: TNEDbeginStory
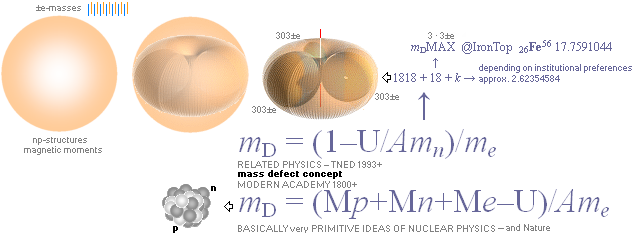
Jämför
etablerat:
MASS
DEFECT DEFINITION IN PHYSICS AND CHEMISTRY, Nov2019 www.thoughtco.com:
In
physics and chemistry, a mass defect refers to
the difference in mass between an atom and the sum of the masses of the
protons, neutrons, and electrons of the atom. This mass is typically associated with the binding energy between
nucleons. The missing mass is the energy released by the formation of the atomic nucleus.;
As
interpreted: mD = Mp + Mn + Me U.
Det visar sig att massan hos en given kärna alltid är något mindre än den
sammanlagda massan hos de nukleoner som ingår i kärnan. Skillnaden kallas massdefekt.
Om massdefekten betecknas ΔM samt protonens och neutronens massor
resp. Mp och Mn gäller alltså [Z+N=Amasstalet]
ΔM
= Z Mp + N Mn Mkärna
Massdefekten motsvarar enligt ovan ett energibelopp som kallas kärnans
bindningsenergi och som betecknas B..
CHINESE
PHYSICS C Vol. 41, No. 3 (2017) 030003 The AME2016
atomic mass evaluation, s30003-2sp1ö:
In
general the nuclear masses MN can be calculated from the atomic ones MA:
MN
(A,Z) = MA (A,Z) Z×Me
+ Be(Z). (1)
Nowadays several measurements are conducted
with fully or almost fully ionized atoms.
In such cases, a correction muste be made for the total binding energy of all
the removed electrons Be(Z), which can be found in the table of
calculated total atomic binding energy of all electrons by Huang et al
[10]. Unfortunately, the precision of the calculated values Be(Z)
is not well established, since this quantity (approximately 760 keV for 92U)
cannot be easily measured..
Elaw: Elaw1¦
noMASSorigin
ENERGILAGEN:
ENERGY LAW: mass origin energy
without ultimate cause
is impossible to relate to any idea of
a creation
energy
work can neither be created, nor be destroyed, only converted: mass can be
destroyed through induction giving heat and light because it cannot be created;
gravitatiion mass is not light: light does not connect to kinetics, no
mother god loving way; Se även utförligt från vic-felet.
LJUS KAN INTE SKAPA MASSANS INNEBOENDE
OSKAPADE ENERGILAGEN: UPPHOVSLÖSA STRUKTUR: INTE DESS NATUR: INTE DESS
EGENSKAP: h = mcr = Plancks konstant = neutronen
I
RELATERAD FYSIK GÄLLER den kvantitativt reversibla ordningen E=(m→γ)cc=(m←γ)cc:
men
inte den kvalitativt motsvarande (m←γ): (m→γ)≠(m←γ):
ljus är inte massa; ljus är inte gravitation:
ljus kan inte skapa massans inneboende
oskapade energilagen: upphovslösa struktur;
Så finner vi generellt i modern akademi att
kärnbegreppen i modern akademi gör ingen
åtskillnad mellan kvantitet och kvalitet.
ENERGILAGEN har redan klargjort dessa
detaljer (Inledningsvinjetten):
LJUS är INTE gravitation: ljus har ingen
massa, uppvisar inte centrifugalkraft i gravitella avböjningsbanor;
MASSA KAN INTE SKAPAS därför att den KAN
förintas i värme och ljus: energins bevarande genom induktionen (COEI).
NEUTRINOSPEKTRUM ¦ ENERGILAGEN ¦ Solrandsavböjningarna
från 1919 ¦ COEI ¦ Parannihilation
massförintelsens process
Energilagen och
massbegreppet: Syntes ¦ DiffGRAFERNA
AS EXPLAINED BY RELATED PHYSICS AND
ITS ATOMIC ICONS: May2020
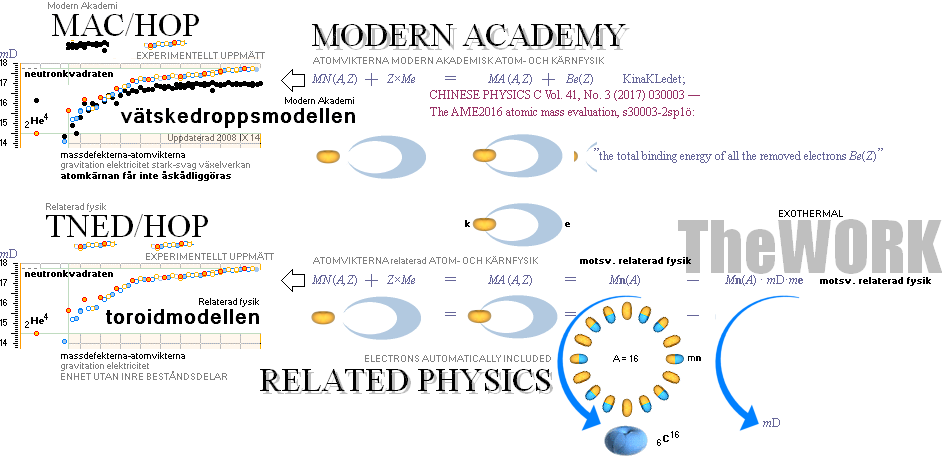
There is no way to physically remove electrons from a parent
atomic nucleus: nuclei and electrons compose the atomic unit. The electrons can
only be attracted to some other location, proportional to the ionizing energy
input (applied strong electric field). Any
electric/inductive excitation energy is still a such, and has no gravitational
representation: no mass. But electrons do have mass; Any idea that excitation
energy (ionization) in mass spectrometry connects to MASS is
a fallacy says TNED. Modern academy has not The Neutron Square: atomic masses
from atomic mass defects a geometrical-physical morphological paragon for
nuclear physics perfectly in line with experimental results. And, as seen:
there is no way to establish a corresponding dialog between the two different
ways in viewing atomic and nuclear physics. Only one of them can explain the
other as a primitive.
TNED ¦ NEUTRON SQUARE Neutronkvadraten
Konventionens/KinaLedets
Be(Z)-faktor har i relaterad mening ingen masskoppling; Den delen ger ett
(mindre) felvärde (som inte är signifikant för den här framställningen, men som
bör noteras):
MODERN
AKADEMI:
massa + massa massa = ENERGI = massa
MN
(A,Z) + Z×Me MA
(A,Z) = Be(Z) ;
RELATERAD
FYSIK:
massa + massa massa = massa ≠
energi : bindningsenergi är
inte vägande massa.
ENERGI massa kan inte relateras ett upphov: energi kan varken skapas eller förintas
endast omfördelas;
Massa kan förintas i värme och ljus därför att den INTE kan skapas:
upphov existerar inte i logiken, säger energilagen;
LJUS ÄR INTE GRAVITATION massa, atomkärnan, gravitationens
fundamentalform och massa gravitation är inte ljus;
Ljusbanor kring gravitationsobjekt utverkar inga centrifugalkrafter:
LJUS HAR INGEN MASSA, KOPPLAR INTE KINETIKEN, inte alls över huvud
taget.
JÄMFÖR KORREKT RELATERAD SKRIVNING:
massa + massa massa = (m→γ)
KINALEDETS
KÄLLTEXT exemplifierar en teoretisk form för beräkning av den angivna Be(Z):
Be(Z) i KeV = (14.4381·Z^2.39 +
1.55468×10^6 · Z^5.35)/1000
KinaKällan s30003-2, ref. Lunney, Pearson and Thibault [11];
Uttryckt
i antal elektronmassor [Be(Z)KeV/511KeV] ges ett lägsta värde
(1H1)
→ Be(Z)KeV/511KeV =
0.0000283, och ett högsta (LBL-tabellens 118Ui293)
(118Ui293)
→ Be(Z)KeV/511KeV = 2.8982892.
Avvikelserna
från de sanna atomviktsvärden (U) blir i motsvarande storleksordning i atomära
massenheter (u)
0.0000000
(obetydligt,1H1-fallet)
0.0015900
(mera märkbart, 118Ui293-fallet Neutronkvadratens värden har
liknande avvikelser). Källtextens exempel med Uran-92 (92U238) på värdet 760
KeV ger i ledet ovan 762.67 KeV eller ett massfel på 1.4925046 elektronmassor i
atomviktsvärdet.
EXEMPEL PÅ EN HÄRLEDD ELEKTRONS ATOMÄRA BINDNINGSENERGI:
Väteatomens jonisationsenergi 13.6 eV ¦
Kortare
TNED-sättet
påstår inte direkt att det konventionella sättet är FEL så bara om det
framhävs vara det enda som finns. Däremot framhäver TNED-sättet att det
konventionella sättet är (ytterst) PRIMITIVT. I förhållande till ett detaljerat
relaterbart natursätt har avgörande delar tagits bort eliminerats. Helheten
har uteslutits och finns inte längre med. Beskrivningssättet utelämnar detaljer
som gör naturbeskrivningen omöjlig: dikterande. Inte härledande.
Experimentalfysiken instrumentmekaniken
visar vägen. Absolut. Men den moderna akademins teorier slutar på rena
spökskepp. Rätta gärna om fel: det finns inte en enda modern akademisk teori
som INTE våldför sig på Naturen.
Det vore intressant, djupt, att få veta att
författaren har fel i den ståndpunkten. Visa.
VAD
BETYDER mNUC=MN(A,Z) vad är det? Här enda kända
relaterade svaret:
mNUC (kärnmassan, begrepp i modern akademisk
kärnfysik) är den rent kvantitativa atommassa som återstår av en
given atom (U) sedan dess elektronhöljesmassa (Zme) avlägsnats,
samt AtomBildningsArbetsEnergins ursprungliga atommassa (mDAme)
har återställts [filmen baklänges: (m←γ)] och
lagts på atom-Minus-Elektron-Mass-Kvantiteten.
Jämför
Neutronkvadratens relaterade sätt det finns inte i modern akademi:
ATOMÄRA MASSDEFEKTEN (mD) är
AtomBildningsArbetsEnergin som användes för atomens
byggnad
uttryckt
(mD i antal elektronmassor via exotermiska E=mcc) som en jämn
fördelning över antalet ursprungliga neutroner (A, masstalet: AVRUNDAT[U/u]):
atomens
massa i KG dividerat med atomära massenheten (u=m[6C12]/12), avrundat
som heltal.
Differenserna mellan U och A är av typen 17.999¦18.0001 → A=18. Noll
felrisk.
Perfekt helhetsbeskrivning utan luckor. mD
= (1 U/Amn)/me.
Atomens kärnladdning (Z) ingår
integrerat tillsammans med atomens yttre elektronbesättning.
Modern akademi har inget liknande. Och
det finns heller ingen korresponderande sambandsform:
Formbegreppet (atomkärnans morfologi) är i modern akademi en primitiv idé,
säger TNED: uppfunnen. Inte härledd.
ATOMKÄRNANS
n-p-struktur ¦ PLANCKRINGEN ¦ PASTOM ¦ LaddningsDeplacementet
Vilket
är det övergripande felet?
Nukleonbegreppet.
Absolut tveklöst nukleonbegreppet. Det finns inga fristående nukleoner i
atomkärnan. Jämför återigen Inledningen.
Används den begreppsformen bokstavligt leder den ofelbart till en djupgående
feluppfattning av kärnfysikens natur. Nukleonbegreppets enda rationella
innebörd i relaterad fysik kopplar atomkärnans n-p-struktur som reglerar
kärnladdningen: det finns inga protoner i atomkärnan, och heller inga
neutroner, endast en väv av ±e i form av fraktala Planckringar (h=mcr):
toroidringar i obegränsad fraktal utsträckning (PASTOM) som reglerar kärnans
toroida ytstruktur (laddning, magnetiskt moment): ![]() .. och som möjliggör inväxlingsfenomen (med
tillräckliga triggande energier) av typen antipartiklar: n-p omvandlas till
p-n under excitationsperioden. Utförliga härledningar i PLANCKRINGEN.
.. och som möjliggör inväxlingsfenomen (med
tillräckliga triggande energier) av typen antipartiklar: n-p omvandlas till
p-n under excitationsperioden. Utförliga härledningar i PLANCKRINGEN.
Med
Järntoppen (26Fe56) = mDmax som ytterligare exempel framträder
helt olika preferenser i toppvärdet för
själva
begreppet massdefekt dialog saknas.
DIFFERENSERNA MÄRKS TYDLIGAST I
ORDNINGEN FÖR DEN SÅ KALLADE JÄRNTOPPEN: nuklidkartans morfologi:
ORDNINGEN OVAN UNDERST refereras också i PDF-dokumentet
CHINESE PHYSICS C Vol. 41, No. 3
(2017) 030003 The AME2016 atomic mass evaluation, s30003-3sp1ö:
The highest
binding energy per nucleon is observed for 62Ni, followed sequentially by 58Fe
and 56Fe..
Vad
är haken?
Jämför återigen inledningsvinjetten[]: Atomkärnan gravitationens fundamentalform
innehåller inga fristående separata partiklar. Kärnfysiken gravitationens
fundamentala form har ingen sådan morfologi. Det är tydligt att också
naturformerna avspeglar/illustrerar/påpekar den fingervisningen.
GRAVITATIONENS
FUNDAMENTALFORM ¦ Järntoppen ¦ StabDIFF ¦ Vattendroppen
som åker på vattenytan elementär kärnfysik
Beteckningar
T¦t förenklar 10±
U = m(Z=atomnummeratomA=masstal)/(u=1.66033 t27 KG = m[6C12]/12) = atomvikt; U=m/u; m=Uu.
U i
konventionell litteratur kallas (eng.) relative isotopic mass (WIKIPEDIA
Atomic mass [Maj2020]: U=m/u).
Beteckningen
U finns inte i konventionell litteratur: eftersökt, inte upphittad.
u i konventionell litteratur (WIKIPEDIA Atomic mass
[Maj2020]
= 1.660
539 066 60(50) t27 KG = atomära massenheten betecknas 1 Da, 1
Dalton efter John Dalton (1766-1844), atomteorins grundare inom kemin.
INSTRUMENTEPOKENS
STANDARDVÄRDEN (1960-1999) KONTRA
DATOREPOKENS
STANDARDVÄRDEN (2000+) exemplifieras och belyses i SOLENS FOTOMETRISKA EFFEKT:
Jämförelse/test/utvärdering TNED, relaterad fysik endast görs mellan de
bägge epokernas marginellt något olika värden i beräkningen av Solens
fotometriska effekt tillsammans med det IAU-uppmätta och standardiserade
värdet. Instrumentepokens värden ger fullträff, medan datorepokens värden
missar målet. Jämförelsen är ägnad att understryka ämnesinnehållet: begreppet
EXAKTA EXPERIMENTELLA VÄRDEN beror av olika metoder; De olika
anordningarnas interna preferenser (»utvecklas i tiden» med tekniken .. på
gott och ont).
Av
de skälen håller vi oss här helt och hållet konsekvent till de redovisade instrumentepokens
standardvärden som primära referenser så att tillfället för jämförelser
bevaras.
JÄMFÖR:
Det
har tagit runt 40 år att sammanställa atom och kärnfysiken i TNED: Vi kan
(alltså) inte hålla på och vela med ändringar under tiden arbetet fortlöper
allt eftersom Societeten Uppfinner Nytt: Vi håller oss istället till »gamla
hederliga instrumentvärden» och testar SEDAN dessa löpande tillsammans med
societetens nya datoriserade bevekelsegrunder så länge
instrumentmekaniken håller måttet. Vilket den uppenbarligen har gjort hittills.
Annars går vi hem.
mn neutronmassan 1.0086652u
me elektronmassan 0.000548598u
INSTRUMENTEPOKENS
ANVÄNDA STANDARDVÄRDEN ¦ Jämförande
DATOREPOKENS STANDARDVÄRDEN ¦ Konstanterna
SOLENS
FOTOMETRISKA EFFEKT ¦ IAU
framträder klockren fullträff ¦ TNED
FEfullTNED: Inledning
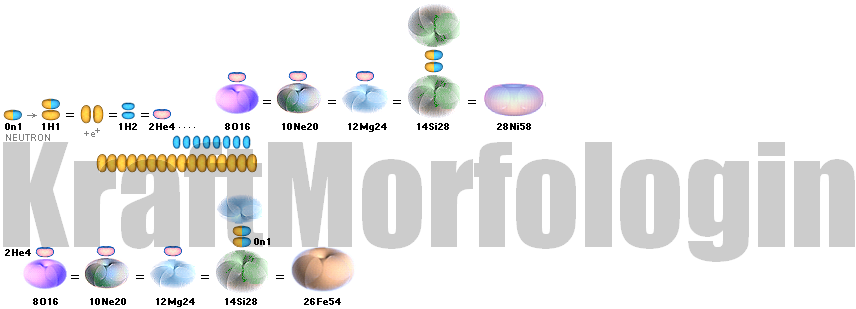
FUSIONSELLIPSERNAS FULLSTÄNDIGA FÖRKLARING
I TNED INLEDANDE EXEMPEL
HUR LÄTTA NUKLIDGRUPPENS NUKLIDER KAN
DEFINIERA TUNGA NUKLIDGRUPPENS EXOTERMSISKA NUKLIDBILDNINGAR
INLEDANDE SAMMANSATT EXEMPEL SOM
VISAR och bevisar ÄMNETS CERTIFIERADE ÄKTHET se även komplementen i BERYLLIUMKLACKEN och 3Li8-nukliden:
Atomindividernas ikoniserade grundnuklider/fusionsagenter
enligt TNED:

DOTS: EXPERIMENTALLY MEASURED ATOMIC
MASSES by U = Amn(1 mDme)
INLEDANDE
BELYSANDE EXEMPEL fusionsleden ovan beskriver resultatbilden nedan.
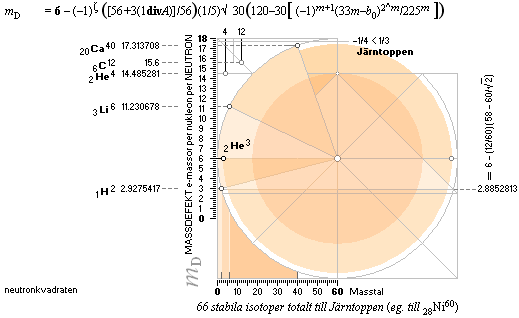
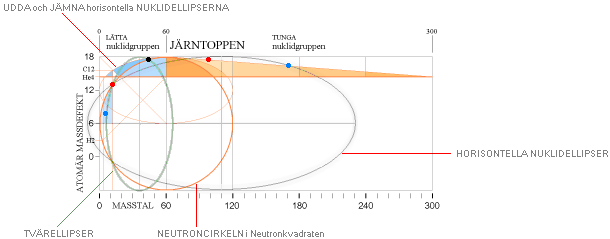
NEUTRONKVADRATENS KÄRNFYSIK:
Fusionsleden
sammanställda ovan illustrerar den övergripande resultatbilden nedan.
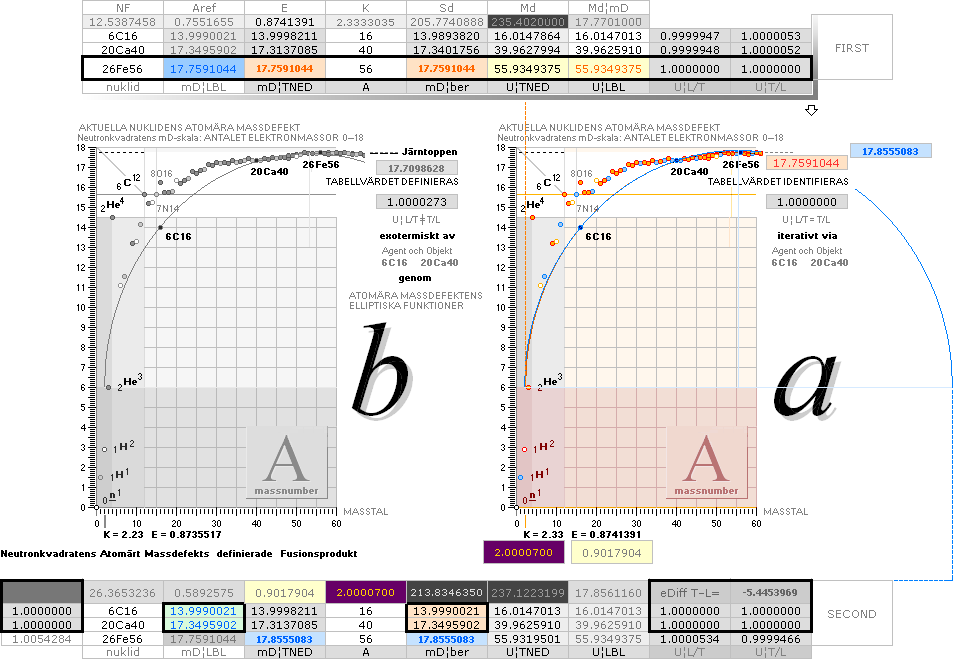
Tabell 1 O61 hExoterm2020test.ods
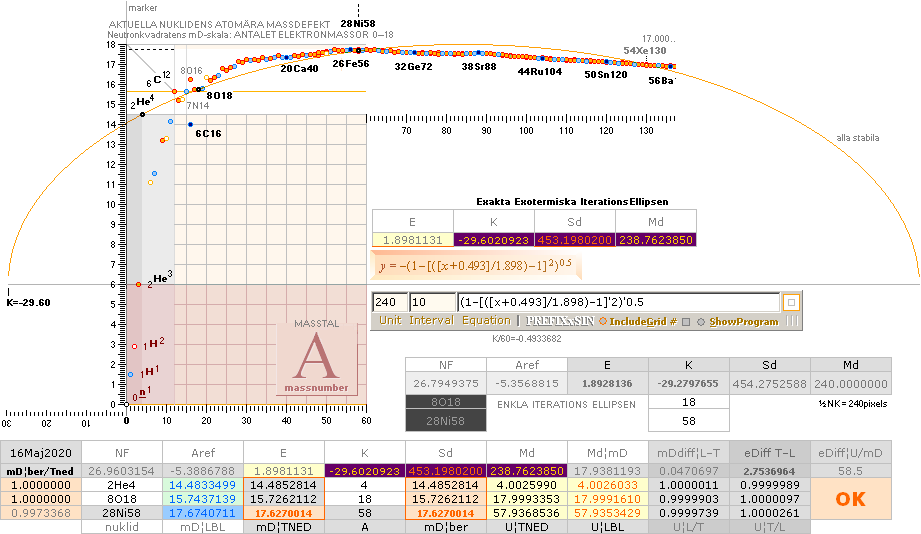
ITERATIONSellipsens
egna mD-värde för 28Ni58 från egna NK-bestämda
2He4¦14.4852814 och 8O18¦15.7262112 : 28Ni58¦17.6270014
Illustrationens skara av färgade små
ringar representerar tabellverkens samtliga stabila nukliders atomvikter U
omräknade i atomära massdefekter mD=(1U/Amn)/me.
Utsträckningen till max A=300 är
större än (ordinära) fönsterbredden och avkortas därför här illustrativt från
fall till fall beroende på aktuell tillämpning.
ITERATIONEN HÄR HAR GJORTS
MANUELLT den är ytterst krävande (visst stimulerande). Men det tar TID för
att komma fram till att 1.0000000 = 1.0000000. Alla decimaler.
18Maj2020: mD¦ber/TNED i
kalkylremsan vänster visade sig kunna snabba upp iterationen via K Sd och Md
betydligt genom att skriva ut skillnaden R = övre undre i tomrutan underst;
Slutvärdet för den ska bli: R = 0.0000000. Med koll på den itereras K Sd och Md
betydligt snabbare genom att R-värdet kan visa negativt¦positivt: man får veta
direkt åt vilket håll iterationen på aktuell parameter ska göras dessa växlar
stundtals riktning under processen vilket utan R-rutan i bland kan bli så
frustrerande att man vill gå Hem. Länge. Alltid. Med R-rutan görs iterationerna
nu manuellt inom 10 minuter.
Den allra
första, ingen R-ruta, tog tre timmar.
EXPERIMENTELLA ATOMVIKTSVÄRDENA I HOPKÄLLAN (LBL, CODATA
med här obetydliga avvikelser från HOP men med betydligt flera individvärden):
HOP ¦ INSTRUMENTEPOKENS
ANVÄNDA STANDARDVÄRDEN ¦ Jämförande
DATOREPOKENS STANDARDVÄRDEN
Man
måste (nog) se det för att tro det.
2He4-kopplingen
i exotermiska fusionsellipsens led, figuren ovan, visade sig
överraskande plötsligt efter olika prövningar med uppritning av den enkla
iterationsellipsen (Se ELLIPSITERATIONERNA: den avviker visuellt omärkligt
från figurens mera exakta). Uppgiften gällde att, eventuellt, hitta en
exakt fusionsanalys för
8O18
+ 20Ca40 = 28Ni58. Vi fann den med besked. Vi studerar hela Neutronkvadratens
exotermiska Fusionskomplex grundämnesbildningen från neutronen och uppåt med
försök till förklaring alla detaljer genom särskilda exempel.
54Xe130
54Xe130-atomen
bör också passa in på fusionsellipsen. Vi kan testa den delen genom att direkt
skriva in masstalet 130 för 58 (andra parametrar berörs inte). Resultatet blir,
visar det sig, exakt detsamma som att kopiera hela kalkylremsan med K Sd och Md
värdena, och använda samma agent 2He4 med det nyligen NK-mD-bestämda objektet
28Li58 samt den sökta fusionsprodukten 58Xe130: NKmD(58Xe130) = 16.8956866.
Atomvikterna i slutänden skiljer sig i relationstal på 58.2 miljondelar. Eller
med differensen i antal atomära massenheter: 0.0007568u (=+1.38 elektronmassor).
Tabell 1 O101 hExoterm2020test.ods

Inte en enda knapptryckning utöver
det.
Allmän
metodbeskrivning
Vi
utnyttjar tillgängliga tabeller (HOP, CODATA, LBL) med atomvikter för att
bevisa fusionsellipsernas allmänna och generella förankring: atomvikternas
koppling till Neutronkvadratens elliptiska funktioner. En grovform tas först
fram ut tabellvärdena som visar hur Neutronkvadratens fusionsellipser
inbegriper aktuella fusionsobjekt och deras produkter. Vi kan studera varje
enskilt sådant resultat i de särskilda tabellceller som redovisar kvantiteterna.
Vi använder sedan framräknade motsvarande atomvikter enbart via
Neutronkvadratens anvisningar. Dessa resultat jämförs sedan i slutänden med de
experimentellt uppmätta värdena.
StabDIFF ¦ EllipsIterationerna ¦ FusionsEllipsfunktionernas härledning ¦
FusionsEPSmetod: Insatex
a: Tabellvärden
med atomvikter (U) omräknade till atomära massdefektsvärden mD = (1
U/Amn)/me;
b: Approximerade
förenklade fusionsellipser via tabellvärdena;
c: Fusionsellipsernas
resultatparametrar med redovisade exotermiskt avgivna fusionsenergier i varje
steg.
FUSIONSRINGAR
(G-centrumBegin) kan bara existera i reguljära neutronmasskroppar:
primärkroppar med maximal neutrontäthet (1,82 T17 KG/M³); Atomkärnorna ligger
redan innanför varandras nuklidbarriärer, och fusionerna kan börja så snart
neutronerna sönderfaller; Ljusets g-beroende bestämmer olika sönderfallszoner i
neutronmasskroppen: i centrum där g-potentialen är som lägst och därmed
ljushastigheten som störst sker sönderfallet först och snabbast. Därmed
etableras olika neutronkvoter i spridning genom hela kroppen under den totalt
sett snabba fusionsfasen, vilket garanterar att olika fusionsringar kan bilda
och sammansätta olika slutprodukter i fusionsleden: de färdiga
grundämnesatomerna.
Etablerade teorier om grundämnesbildningen
brottas med stora problem för tyngre atomer än omkring Järntoppen. I TNED
(relaterad fysik) finns inte den problematiken i och med att hela
grundämneskomplexet ombesörjes med början från maximalt materietäta
kroppskomplex som sedan expanderar under fusionsfasen och på den vägen antar
sina normalt slutliga kroppsformer. Den teorin saknas helt och hållet i
etablerade kvarter. man anser där istället att kropparna bildats genom
»singulär uppsamling av nedfallande material under lång tid». Svårigheten att
förklara grundämnesbildningen med den bevekelsegrunden är formidabel. Kortare
sagt: omöjlig. Vissa citat från etablerade verk ges löpande.
Atomkärnans inkompressibilitet ¦ G-centrumBegin ¦ Fusionsringar
EXEMPEL 6C16 ¦ Kurvskaran
till 6C16 ¦
Varför omöjligt, vad är haken?
Tunga
nuklidgruppens atomer kräver exotermiska fusionsagenter (med höga
neutroninnehåll) som normalt är (ytterst) kortlivade: »finns inte i bygden».
Hur så WhatsUp? Etablerad kosmologi har ingen individuellt
kroppskompakt begynnelse: himlakropparna anses bildas FÖRST sedan »allt har
exploderat»: därefter följer, säger man, »successiv sammandragning» (lottovinster
åt alla med en gång). Ett sätt att få ihop det med den bevekelsegrunden
skulle då vara »successiv neutronpåbyggnad». Men inte heller några överdrivet
ymniga neutronkällor finns »i den moderna akademins kosmologiskt exploderade
närbygd». Så, moderna genier brottas med stora (omöjliga) förklaringsproblem.
Kanske det främsta: blotta påpekandet att alla naturliga grundämnen (redan)
finns på/i Jorden.
Största frågorna: syret, vattnet:
livskemin. Vi.
RELATERAD
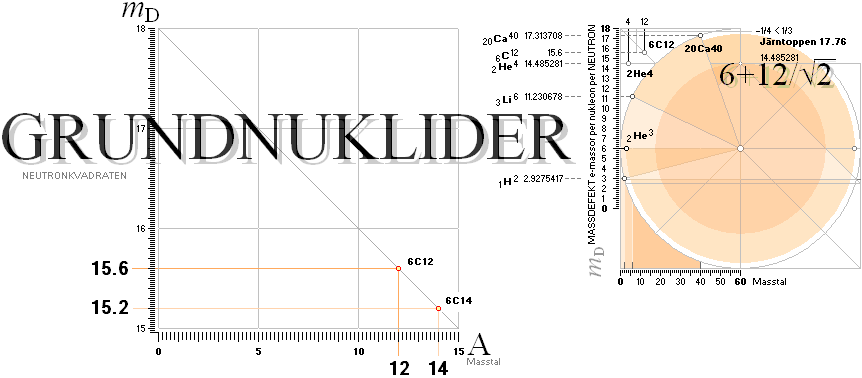
GRUNDATOMFYSIK radioaktiva kolet C14
mD[6C14] =
15.2 = 6 + 12[6014]/60
6C14 är betainstabil [5 700 år]. Den bildas från stabila kväveatomen 7N14 genom kosmisk
strålning: Högenergetiska partiklar från yttre rymden kommer in till
Jordatmosfären och åstadkommer häftiga partikelkollisioner. En del av
fragmenten är neutroner: En sådan som träffar på en kväveatom 7N14 resulterar i
ett utbyte med energiupptag: 7N14 neutraliseras [exciteras] i kärnladdningen på
en elektronladdning till 6C14: den atomen är nu exciterad och kvarstår så med
halveringstiden 5 700 år tills den återigen blir en vanlig stabil 7N14 atom
genom utgivning av den tidigare erhållna extra neutraliserande, exciterande,
elektronmassan från kollisionsögonblicket. Den utgivna elektronmassan tillhör
den kolliderande neutronen med dess egna slutna sönderfallsprodukt, och bildar
i nettoresultaträkningen atom med denna som en väteatom [1H1]. Se även
motsvarande beskrivning i Wikipedia Carbon-14 [FOCUS MATERIEN 1975 s314sp2ö].
Reaktionen skrivs relaterat
motsvarande n → [7N14
= ([p]+e) →
(7e+)N14 = (6e+)C14] → [p] =
6C14(5700y) + (e + [p] = 1H1) + (m→γ) = 7N14 + 1H1.
Konventionellt förkortat: n + 7N14 → 6C14 + p med
sönderfallet 6C14(5700y) + e + v
→ 7N14, v för neutrino. Gammakomponenten (m→γ), generellt neutrinostrålning i relaterad fysik »m till gamma»
(Comptoneffekten garanterar att strålningesfrekvensen avtar med strålningens
växelverkan med materia), är den som normalt den kolliderande neutronen skulle
ge ut i samband med sitt eget naturliga betasönderfall (12-14 minuter) till
stabil väteatom (1H1). Den delen tas istället upp av 7N14 vid kollisionsögonblicket,
och kvarstår sedan som en excitationsenergi med förlängd varaktighet, och som
utges med återgången från 6C14 till 7N14.
Omvandlingen
7N14 → 7N14 blir alltså i netto helt förlustfri: ingen massdestruktion
sker i den stabila 7N14, den ändras inte (»nukleär morfologi»).
Neutronkvadratens egna fasta mD-värde för 7N14 (15.2865494) härleds här i
3Li6-GRUPPEN. 6C14(U=Amn[1mDme]=14.0035¦32) blir alltså
något litet tyngre än 7N14(U=14.0029¦31) med tillägget av en extra elektronmassa plus
massan som åtgår i energin som krävs för att få det återställande arbetet
utfört.
3Li6-GRUPPEN ¦
Neutrinospektrum ¦ Comptoneffekten illustrerad ¦ 6C12 ¦ Neutrinostrålning ¦ ComptonEffekten illustrerad
Neutronkvadratens
grundnuklider framträder genom kvadraturens egen inneboende enkla
mönstergeometri.
Kvantiteterna
identifieras uteslutande enbart genom
elliptiska
funktioner från atomära massdefektens mD = (1U/Amn)/me
härledning via certifierade
experimentellt uppmätta atomvikter U = Amn(1
mDme).
Inte förrän jämförande experimentellt grundade tabellverk finns kan
Neutronkvadraten bevisas.
Elaw1: eLAW
MASSA (m) SAKNAR UPPHOV
föreställningen
om ett världsallt med ändlig begränsad massa, en yttersta skapelseakt, saknar
logisk och rationell fysisk soliditet
DÄRFÖR ATT ENERGIN GÖR DET
energi
kan varken skapas eller förintas, endast omfördelas: frågan om en energins,
massans, begynnelse och början, ett upphov, är en tankevilla, en sinnets
förvillelse
Rätta gärna om
fel (noMASSorigin): Det går inte är logiskt intrinsiskt omöjligt att relatera ett yttersta
upphov
till massans
existens på energilagens kredit: energi kan varken skapas eller
förintas,
endast
omfördelas. Upphov saknas. Ifrågasätt gärna relaterat: Eftersökt. Inget
upphittat. Än.
ALLMÄNNA
GRUNDER INOM DEN RELATERBARA (TNED) KÄRN- OCH ATOMFYSIKEN
Begreppet
Atomär Massdefekt finns inte inom modern akademi modern akademi använder
uteslutande begrepp som baseras på atomens kärna: MD = Z·Mp +
(N=AZ)·Mn Mkärna,
ref. FMs124sp2ö,
motsvarar kärnans bindningsenergi. I relaterad fysik finns inget
sådant motsvarande begrepp:
Atomkärna + Elektronhölje = Atomen som en enhet; Modern akademi anser
att »elektroner skapas» medan relaterad fysik påpekar att elektroner kommer ur
neutronens sönderfall = inifrån neutronen = den neutrala fundamentala massform,
gravitationsfundamentet, vi kallar för en atom (i formen av en kompakt
atomkärna). Neutronens naturliga instabilitet (normalt inom 12-14 minuter)
resulterar i ett sönderfall: en stabil väteatom bildas:
atomkärna
+ (atomhölje=elektronhölje).
Relaterad
fysik innefattar inget begrepp om nukleär massdefekt det finns ingenting sådant i relaterad fysik därför
att atomkärnan är partikelfri: inga »fristående neutroner och protoner»
existerar i atomkärnan. Det är en vanföreställning se särskilt ovan från
inledningen. Massdefektsbegreppet berör hela ATOMEN. Toppvärdet nås vid
JÄRNTOPPEN.
JÄRNTOPPEN ¦ Precisionsgränsen 1.0008 ¦ TNED
mD = (1 U/Amn)/me
atomära massdefekten i antal elektronmassor ingår inte i modern akademi;
U atomvikten i u-enheter: 1u = 1.66033 t27 KG = 1/12 av 6C12-massan;
A masstalet antalet ursprungliga neutroner (med
intern strukturfördelning i n och p »antal neutroner och protoner»);
mn neutronmassan i u-enheter: 1.0086652;
me elektronmassan i u-enheter: 0.000548598;
U/Amn är verkliga
atomvikten (U) genom ursprungliga neutronmassmängden: U alltid den mindre;
1
U/Amn är massförstörda neutronmängden (m→γ) som
användes till arbetet för att bygga U-atomen;
(1 U/Amn)/me
är ekvivalenta elektronantalet för byggmassan (m→γ)
till U-atomen: atomära massdefekten.
Fusionsellipsernas
prövningsvärden möjliga exotermiska fusioner genom iterationer
I
prövningarna insätts godtyckligt utan mera ingående fusionsanalyser
massdefektsvärden från redan genomlysta atomnuklider.
(Fusionsanalyserna hur en produktnuklid
bildas exotermiskt från en given fusionsagent med fusionsobjekt, flera olika
vägar finns kan vara krävande, som det har visat sig, och det är inte
alltid man ser lösningarna med en gång om alls ..)
Resultatbilden,
om alls relevant, utpekar sedan eventuellt vidare kandidater som passar in på
experimentellt uppmätta värden med en garanterad atomviktsprecision i
relationstal
EXPERIMENTELL/BERÄKNAD
mindre än precisionsgränsen 1.0008 eller större än dess invers 1/1.0008
= 0.999200639 vi ser helst värden av typen 1.0000nn och mindre mot 1 vilket
visar relevanta resultat ju större precisionen är.
Varför är den barnsliga mönsterkvadraturen viktig? Därför att
hela atomens balanserade dynamik (tydligen: detaljerad härledning) är grundad
på resonanser hela tal (Se HÄRLEDNINGEN TILL PERIODISKA SYSTEMET från
KEPLERRESONANSERNA) och hela kärnan på utpräglade Q-parsymmetrier (±e):
parsymmetrierna styr i kraft av energivillkor formerna för stabilitet och
jämvikt (atom- och kärnfysikens två kungsekvationer [impuls och kraft]).
Och därmed en uppenbar självservering till den matematiska geometrin:
Kärnformen avspeglar symmetriformen och därmed den atomära
massdefekten (mD) som definierar atomvikterna (U=nu) ur masstalen
(A) via elektronresonanserna (periodiska systemet):
Om vi kan finna den mönsterformen, mera exakt, bör den följdriktigt
utpeka atomvikterna
via massdefekterna från rena
geometriska koncept!
Det gör den också!
Periodiska
systemets härledning ¦ KUNGSEKVATIONERNA
för atom- och kärnfysiken i TNED ¦ Allmänna
ATOMÄRA Massdefektsekvationen i TNED
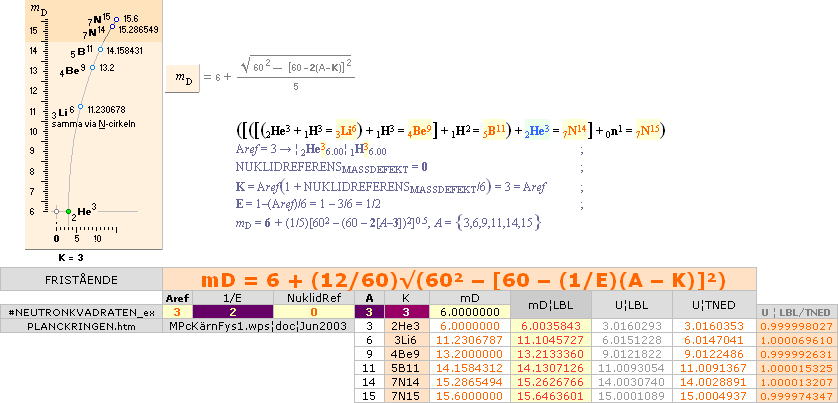
NEUTRONKVADRATENS HÄRLEDNING
INNEFATTAR ELLIPTISKA EKVATIONER SOM DEFINIERAR NUKLIDBILDNINGEN GENOM
EXOTERMISKA KÄRNREAKTIONSLAGEN MEN ÄMNET STÅR FULLKOMLIGT OREPRESENTERAT I
MODERN AKADEMI. Hur har det kommit till? TESTA SVAR: Därför att modern akademi
under sin uppsegling 1800+ föresatte sig att leka Herre Över Universum
inskription på medaljongen till matematikernas förnämsta utmärkelse genom att
UPPFINNA fysiken. Inte HÄRLEDA den ur REDAN INTELLIGENT FRAMSTÄLLDA
detaljerat bevisbara PRINCIPER. Säg igen. Berätta. Undervisa oss: Relatera.
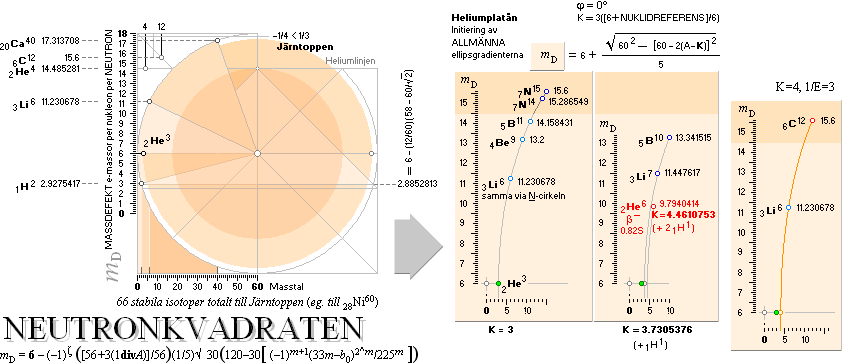
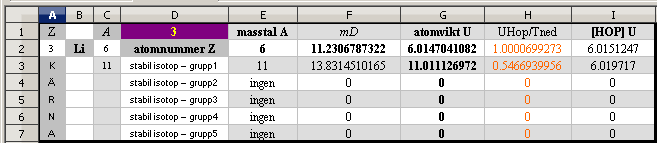
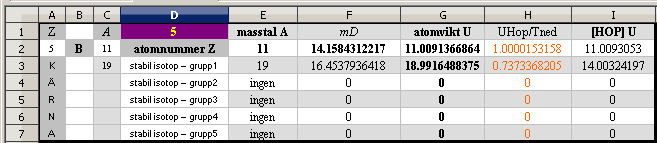
EX: Aref = 3 = K
= 6(1 E) = Aref(1 + NUKLIDREFERENSMASSDEFEKT/6) ¦ NUKLIDREFERENSMASSDEFEKT = 0 ¦ E = 1
K/6 = 0,5 ¦ E = 1(Aref)/6 ¦ A={6;9;11;14;15}
![]()
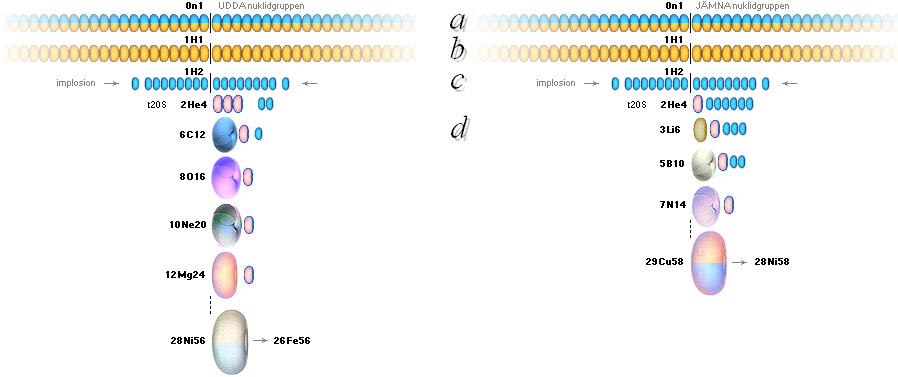
Basnukliderna från neutronen 0n1 upp mot
Järntoppen 26Fe58 har egna mönsterrelaterade fasta mD-värden som framgår ur
Neutronkvadratens egen fasta och fixa mönstergeometri överensstämmelsen med
redan experimentellt uppmätta värden är slående. Se STABDIFF. En del av dessa
framgår direkt via Neutroncirkeln, en del andra via Fusionsellipserna
exemplifierade i tre fall ovan. Från dessa, med ytterligare härledda eller
itererade fusionsellipser kan vi luska ut mD-värdena för tyngre atomgrupper
och därmed de motsvarande reella atomvikterna för i princip samtliga möjliga atomer. Men byggprincipen (här i
relaterad fysik) med tyngre från lättare förutsätter enbart exotermiska
fusioner ett stort problem i modern kosmologisk teori för alla atomer i den
tunga nuklidgruppen, de efter Järntoppen. I TNED blir den självskriven genom
himlakroppsbildningen som grundad på maximala neutronmasskroppar på atomkärnans
garanterade inkompressibilitet: max neutronmassatäthet är Dmax = 1,82 T17
KG/M³. Exempel följer.
FUSIONSELLIPSERNAS
HÄRLEDNING ¦ ATOMÄRA
Massdefektsekvationen originalet från 2003 ¦ Dmax ¦ Atomkärnans inkompressibilitet ¦ TNED ¦ STABDIFF ¦ K-cellens Expansion
Neutronkvadratens
kärnmatematik måste hanteras strängt med början från mD=0, neutronen, och uppåt
med hjälp av de givna fasta och fixa masstalens mD-värden. Dessa är flera och,
som ovan, utpekas av neutronkvadratens egen specifika mönsterform. Det går INTE
att »hoppa in var som helst» utan Viss »Vägledning av Befaren»: Komplexet
fungerar som En Slags Växt: måste börja nerifrån roten (fröet).
Neutronkvadratens
Exempelformer:
GRUNDNUKLIDER INOM LÄTTA
NUKLIDGRUPPEN masstal A=1-60:
Kalkylkorten nedan
beräknar mD via den givna sambandsformen genom inmatning av respektive
nuklids masstal A.
Analysen utgår från
Neutronkvadratens givna mD-värden. Dessa byggs sedan på uppåt till
tyngre nuklider med samtidig koll på Exotermiska Kärnreaktionslagen som
garanterar att fusionen är exotermisk, annars går det inte vars mD-värden
SÅ beräknas från de enkla basnukliderna.
Kalkylkorten nedan är sammanställda från
resultaten i grundarbetena (2003+), samt en del ytterligare (Apr2020) för att
visa och bevisa (jämförelser med resultat från den moderna akademins teorier)
Neutronkvadratens praktiska ställning inom experimentalfysikens uppnådda
resultatvärden.
GN: NK
Grundnukliderna i
TNED-Neutronkvadraten 1H1 1H2 1H3 2He3
2He4
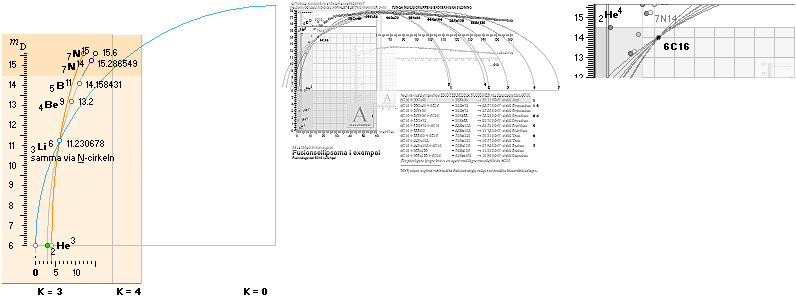
Tabell 1 C52 hExoterm2020test.ods
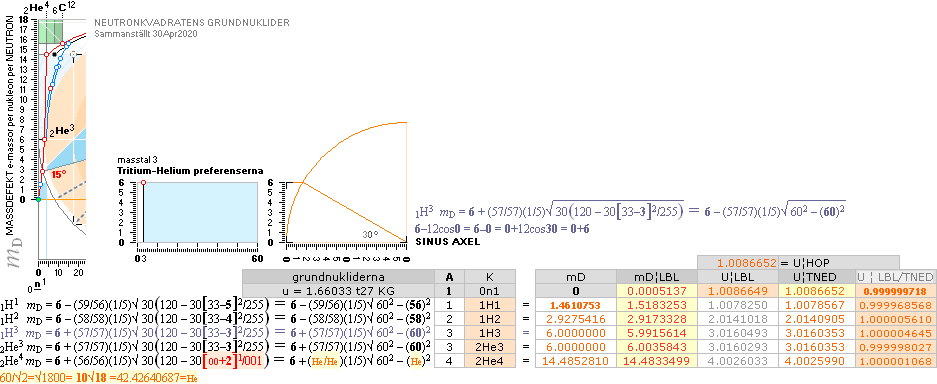
mD(2He4) = 6 + (12/60 = 1/5)√1800 = 6 +
(60/√2)/5 = 6 + 12/√2 = 6 + √72 = 6 + 2√18
= 14.48528137..
![]()
½NK-tvärellipsens
egna mD-värden: 1H1¦1.4610754 1H2¦2.9275417 1H3¦6.0000000 2He3¦6.0000000 2He4¦14.4852814
mD = 6 ± .. :
FUSIONSELLIPSER
SOM FÖRENAR NUKLIDAGENTER I LÄTTA NUKLIDGRUPPEN
här särskilt (enbart) 1H1 och 1H2 just beträffande deras 6
MINUS i mD-formen (teckenvillkor)
kräver särskild
uppmärksamhet i fusionsellipsernas beräkning och kontroll:
Se FUSIONSEXEMPEL.
Med de två enda minus-kandidaterna 1H1 och
1H2 i allmänna massdefektsekvationen 6 + EKV blir enda åtgärden att införa 6 +
(SIGN[A3])·EKV ; SIGN[A3] för A={1;2} ger MINUS1, övriga PLUS1.
Tidigare
framställningar i Universums Historia har (explicit) inte fokuserat på den mera
allmängiltiga lösningsmängden (inga föregående exempel i UH av den typen).
Här ges en mera
fullständig genomgång.
Erinra f.ö.
fusionskomplexets begränsningar: max 3 nuklider i varje STEG typ ABA är
alltid möjliga i primärkropparnas maximalt tätt liggande primära neutronpackningar
före neutronsönderfallet;
mellankärnan
B spärrar effektivt Coulombkrafterna i spinnaxlarnas riktning mellan AA så att
fusioner alltid sker korrekt spinnsynkroniserat på ändplattor typ A¦B¦A, eller
för ett par A¦B.
NEUTRONKVADRATENS 60-GRÄNS
I sammanställt bildkopierat
utdrag från originalet 23VI2003 MPcKärnsynt.wps
i MsWORKS 4.0 med Windows 3.1:
MsWORKS med dess kalkylprogram förbjöds (vandaliserades/vanställdes/spärrades) av Microsoft 2008 för vidare datoranvändning
FÖRETAGETS PERSONAL KAN
INTE HANTERA DATORER, DATORUTVECKLING, DATORSTÖDD VETENSKAP. Rätta gärna om
fel: förstår inte konceptet. Tydligen.
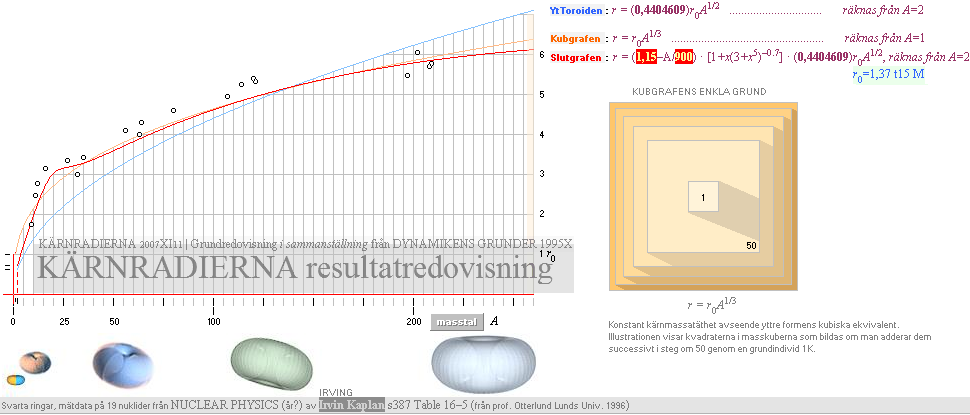
60-skalan ¦ DEUTERONENS
HEMLIGHET 1/√2 impulsmomentets bevarande¦ KÄRNRADIERNA ¦
PREFIXxSIN (R2)/R = sinA = 12/R ¦ R =
2/(1[sinA=15°]) ¦ r0 = 1.37 T15 M:
Neutronkvadratens 60-skalan ger reguljära
neutronkvadratens mD(1H2) = 6 0.2√ 60² 58²
=
mD = 2.92
754 170 med U = 2.01 409 047. Motsvarande
experimentellt uppmätt HOP ger
mD = 2.91 693 323 med U = 2.01 410 222. TNED-medelvärdet: (2.92 754 17 + 2.89 417 14)/2 = 2.91 085 655.


1H2 Neutronkvadraten
TNED relaterad fysik 2020V7
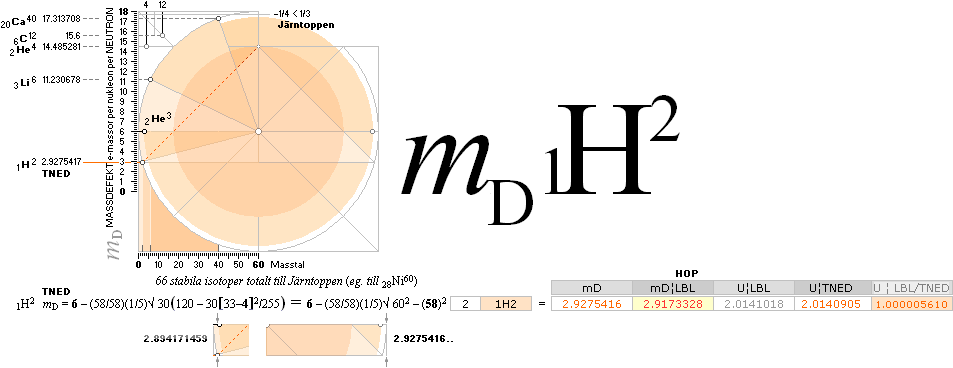
NEUTRONKVADRATENS FUSIONSELLIPSER
I PRAKTISKA EXEMPEL hur neutronkvadraten
definierar atomvikter ur beräknande atomära massdefekter
Sammanställningar
genom kalkylkort jämförande resultatvärden TNED/Experimentalfysiken vi för
resonemangen (en del vidlyftiga) delvis successivt i det följande:
Tabell 1 A61 hExoterm2020test.ods
![]()
½NK-tvärellipsens
egna mD-värden: 2He3¦6.0000000 3Li6¦11.2306787 4Be9¦13.2000000 5B11¦14.1584312 7N14¦15.2865494 7N15¦15.6000000
NEUTRONKVADRATEN
exempel ¦ Jämförande
diagram CODATA/HOP
minstEXOTERMISKT AVGIVEN FUSIONSENERGI:
1H1+1H2 →¦ 2He3:5.45MeV
¦ + 1H3 →¦ 3Li6:15.66MeV ¦ + 1H3 →¦ 4Be9:17.54MeV
¦ + 1H2 →¦ 5B11:15.68MeV
¦ + 2He3 →¦ 7N14:
20.56MeV ¦ + 0n1 →¦ 7N15: 10.74MeV ¦ sma: 85.63 MeV
VAD VISAR OCH BEVISAR
EXEMPLEN?
Kosmologins
fundamentala huvudfråga: GRUNDÄMNESBILDNINGEN.
I modern akademi (BONNIERS ASTRONOMI 1978 ger en del fusionsexempel) kan man inte
härleda EXOTERMISKA (som ger energi ¦
endotermiska kräver energi) FUSIONER
bildningen av tyngre
atomer från lättare
över Järntoppen
(masstal A vid max 60).
Varför inte? Max tätt liggande inkompressibla atomkärnor från ruta ett ingår inte i modern akademi.
TNED klarar det (galant) vi återkommer
strax dit (Grundämnesbildningen).
BONNIERS
ASTRONOMI 1978 ¦ GRUNDÄMNESBILDNINGEN ¦
2He6 8O17
¦ (8O17)II
Tabell 1 B71 hExoterm2020test.ods

½NK-tvärellipsens
egna mD-värden: 2He6¦9.7940414 8O17¦15.7579575
3Li7 5B10

½NK-tvärellipsens
egna mD-värden: 3Li7¦11.4476176 5B10¦13.3415157
När temperaturen nått
ända upp till 4 × 109 K har nästan samtliga kärnor omvandlats
till isotoper kring järntoppen.,
Här slutar
uppbyggandet, eftersom varje fortsatt fusion kräver ett tillskott av
energi; för att de grundämnen som är
tyngre än järn skall uppstå krävs alltså andra processer., BAs123sp1mn.
Tabell 1 C81 hExoterm2020test.ods

½NK-tvärellipsens
egna mD-värden: 3Li6¦11.2306787 6C12¦15.6000000
Testa gärna annat: Vi
vet (genom exempel) att en specifik grundnuklid kan bildas på flera (många) olika
sätt (beroende på antalet ingående neutroner, den här benämnda s.k.
neutronkvoten). Här ges endast enstaka (mest framträdande) exempel.
KOLLISIONSFUSIONER det
enda modern akademi förfogar över i sin kosmologiska teoretiska idé om
grundämnenas ursprung genom successivt stegrad temperatur säger modern
akademi. Men bara upp till en viss gräns (Järntoppen, konv. T = 4 T9 °K). Stjärnor
kan inte bilda högre temperaturer, enligt modern akademisk teori:
.. för att de grundämnen
som är tyngre än järn skall uppstå krävs alltså andra processer., BAs123sp1mn.
4Be9 6C13 8O16 (4Be8)
Tabell 1 C86 hExoterm2020test.ods

½NK-tvärellipsens
egna mD-värden: 4Be9¦13.2000000 6C13¦15.2204989 8O16¦16.2499951
För Aref=3.5, se härledningarna i TVÄRELLIPSENS
DYNAMIK ¦ BerylliumKlacken ¦ Helium3Syntesen ¦ ATOMÄRA MASSDEFEKTEN
DET FINNS KNAPPAST FLERA SÄTT ÄN ETT ENDA MATEMATISKT
SÅDANT för härledningen till grundämnenas möjliga exotermiska uppkomst.
Nämligen med
början från ATOMÄR MASSDEFEKT lika med 0: neutronen. Sedan vidare som en VÄXT:
stadigt och strängt nerifrån och uppåt, utåt.
Den som menar
annat får gärna träda fram med tydliga exempel.
Litteraturen (BA) är rik
på referenser och sticker inte under stol med att många, och svåra, frågor
återstår att lösa »innan man (helt) förstått uppkomsterna».
Så är, för att nämna exempel vägen från
järnets masstal 56 till den mest förekommande naturliga uranisotopen 92U238
med atomära massdefekten 15.26 e-massor per nukleon per neutron tämligen lång.
Det är ingen enkel gåta hur det har gått till med den moderna akademins
kärnteoretiska kosmologiska preferenser.
Att rent teoretiskt plocka på
befintliga nuklider ur helium-järnspektrat med neutroner i snabb takt och
därigenom få befintliga grundämnen genom olika sönderfall verkar inte vara
några större problem. Neutronen har massdefekt noll exakt, så den kan
omedelbart betjäna vilken fantasiverkstad som helst om det gäller avdelningen
snabba teoretiska fusioner.
Problemet är hur det gått till i praktiken:
marken vi står på.
Neutronkällorna växer inte precis på
träden. Heller fungerar inte vilka som helst neutronbombardemang i praktiken.
2He6 8O17
¦ (8O17)a
möjligen; 1H1 →
0n1 ← 1H1 = 2He3 = 1H1 + 1H2: nuklidreferensen kan återföras på en
typ mD(2×1H1 + 0n1 = 2×1H1) ¦ Aref=3:
Tabell 1 B93 hExoterm2020test.ods

½NK-tvärellipsens
egna mD-värden: 2He6¦9.7940414¦5 8O17¦15.7579575¦6
EXEMPLEN VISAR OCH BEV ISAR ATT DEN HÄRLEDANDE ORDNINGEN KRÄVER EN
MINUTIÖST NOGGRANN GRUNDFORM MED VÄL RELATERBARA NUKLIDREFERENSER SOM TILLÅTS VÄXA NERIFRÅN OCH UPPÅT PÅ REDAN
GIVNA PREMISSER.
FÖREKOMMER FEL I ANALYSEN, VISAR DET SIG DIREKT I GALNA
VÄRDEN vi testar alltid resultaten mot experimentellt uppmätt, om
tillgängligt.
En förklaring till
många tunga grundämnens uppkomst är att de skulle ha byggts upp gradvis genom
neutroninfångning., BAs123sp1mn.
9F19 10Ne20
Tabell 1 B97 hExoterm2020test.ods

½NK-tvärellipsens
egna mD-värden: 9F19¦15.8054367 10Ne20¦16.2023393
Helium3Syntesen ¦ KÄRNRADIERNA ¦ Väte-HeliumKopplingen
60-skalan ¦ GRUNDNUKLIDERNA ¦ NEUTRONKVADRATENS BASVÄRDEN ¦ N3m20-härledningen
Uppgiften på Väte 1H1¦1.52 [HOP 1.5180399] anges i
förekommande fall som tabellverkets experimentella make medan
Neutronkvadraten för sin del utpekar ett värde genom Neutronkvadratens
alternativa allmänna atomära massdefektsekvation, se NEUTRONKVADRATENS
BASVÄRDEN,
mD = 6 (59/56)×(12/60)×ROT(60² 56²) = 1.461075377:
Kopplingen till 56 ges via VÄTE-HELIUMKOPPLINGEN ¦ GRUNDNUKLIDERNA masstalet 4 = 6056 med referens till DE
LIKA KÄRNRADIERNA för Vätekärnan och Helium-4-kärnan enligt N3m20-härledningen
och dess koppling till KÄRNRADIERNA.
Det finns
alltså något olika preferenser här som kan användas för att testa olika
slutresultat. FÖR ATT GÖRA ANALYSEN RÄTTVIS, ANVÄNDER VI här ENDAST NEUTRONKVADRATENS
N3m20-REFERENSERNAS VÄRDEN FÖR ATT INTE BLANDA IHOP REFERENSERNA MED REDAN
GIVNA ATOMVIKTSVÄRDEN FRÅN EXPERIMENTELLA MÄTNINGAR frånsett
grundkvantiteterna för neutronmassan och elektronmassan [HOP] och atomära massenheten som vi
inte kan undvara.
Varifrån de neutroner
och protoner som möjliggör dessa processer egentligen kommer är ovisst, men det
är möjligt att de produceras i stora mängder i de senare stadierna av
stjärnornas utveckling, eller också kan kanske allt detta ha hänt under
alldeles speciella betingelser i början av Vintergatans utveckling., BAs123sp2n.
Kanske är ovisst möjligt.
Vad säger TNED med bevis
i Neutronkvadratens detaljerade elliptiska funktionsexempel?
Ljusfysikens friställning
från kinetiken (Ljusfrihetssatsen), Ljusfysikens gravitella (GRIP) beroende (DEEP), Atomkärnans
härledning (PASTOM, Planckringen h=mcr, Neutronen), Elektriska laddningens
härledning
ingen av dessa ingår i
modern akademi
visar en helt annan
kärnteoretisk kosmologisk fundamentalgrund:
atomkärnan kan inte komprimeras, den står
redan på noll;
atomkärnans massinnehåller bygger INTE på
volymär (vattendroppsliknande) utfyllnad;
atomkärnans massform (gravitationens
fundamentalform) ligger i YTA toroidfraktaler. Inte i volym.
Det är den främsta
anledningen till, och förklaringen av, att modern akademi missar experimentella
resultat (partikelfysiken) med STORA teoretiska marginaler;
Experimentalfysiken
visar vägen. Men modern akademi ligger långt utanför inblicken i hur det
fungerar. Närmare: Fasansfullt långt utanför.
Rätta gärna om fel.
Absolut.
Tabell 1 C102 hExoterm2020test.ods

½NK-tvärellipsens egna mD-värden: 11Na23¦16.4606692 12Mg24¦16.7759733
MED LEDNING AV GRUNDEXEMPLEN HÄR ALLA FRÅN BÖRJAN I
HELA ANALYSEN (2003) FÅR VI UPPSLAG SOM VISAR HUR EN FORTSÄTTNING MED VIDARE
NUKLIDSERIER KAN REALISERAS: analysen är tveklöst sammansatt, den kräver en
grundlig förtrogenhet med fusionsbegreppen och deras vissa begränsningar.
Ingen helt enkel söndagspromenad. Men oerhört givande.
Tabell 1 C107 hExoterm2020test.ods

½NK-tvärellipsens egna mD-värden: 13Al27¦16.9493414 14Si28¦17.1991314
Max Neutromasstäthet är (TNED¦Dmax) 1,82
T17 KG/M³.
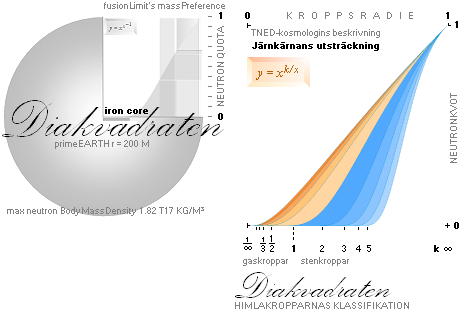
Genom BigBang enligt relaterad fysik, TNED bildas alla himlakroppar från DET maximalt täta
materietillståndet i regi av ljusfysikens gravitella beroende:
K-cellen universum pulserar periodiskt genom
energilagens obevekliga krav på att
inget upphov till massan som energiform kan
relateras, spåras, förstås, härledas eller på annat sätt framställas:
massan som
FYSIKALISK BEGREPP kan inte ges någon förståndsbaserad eller dito grundad
föreställning energilagen om ett »absolut upphov»;
Ifrågasätt attackera påståendet; KRIGA MOT DET gärna: rätta om
fel. Det håller.
den moderna
akademins föreställning om ett universums massa är ändlig har ingen logisk,
rationell, begriplig, relaterbar förankring i förståndet: massbegreppet saknar upphov:
massa har
alltid funnits enligt energins, arbetets, definition.
Tabell 1 C113 hExoterm2020test.ods
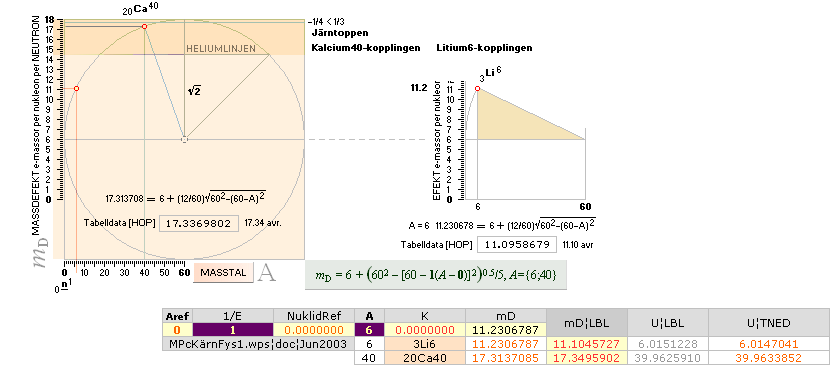
½NK-tvärellipsens egna mD-värden: 3Li6¦11.2306787 20Ca40¦17.3137085
Speciellt genom
(TVÄRELLIPSENS DYNAMIK) Helium-3-syntesen ges särskilda uppslag
Aref behöver nödvändigtvis inte enbart representera hela tal
om hur de
härledda parametrarna i Neutronkvadraten ska eller kan användas för att nå
relevanta resultat; Vi kan bara, i vilket fall, testa validiteten genom
jämförande tabellverk. I här efterföljande sekvenser testas ett sätt att
studera den betainstabila [0.86S→4Be8(5t14S→2[2He4])]
nukliden 3Li8 med dess vidare möjliga primärt exotermiska påbyggnad.
TVÄRELLIPSENS
DYNAMIK ¦ Fusionsanalysen ¦ Helium-3-syntesen ¦ BerylliumKlacken
TYPEN 0n1 → 2He4
[2He5] sönderfaller snabbt inom t21 S [VanNostrands Table 3 2He5]. OM
föreningen flankeras av en närliggande neutron, de två neutronerna bägge inom
och på var sida om Heliumkärnans nuklidbarriär,
0n1 → 2He4 ← 0n1 finns möjligheten för bildning av den mera
långlivade men fortfarande instabila 2He6 [0.82 sekunder].
I primärtillståndets tätt packade neutronregioner finns
säkert den möjligheten helt säkert. Men möjligen på sannolika grunder i
mindre förekommande fall. Principen är dock klar och kan relateras och
utnyttjas som ovan.
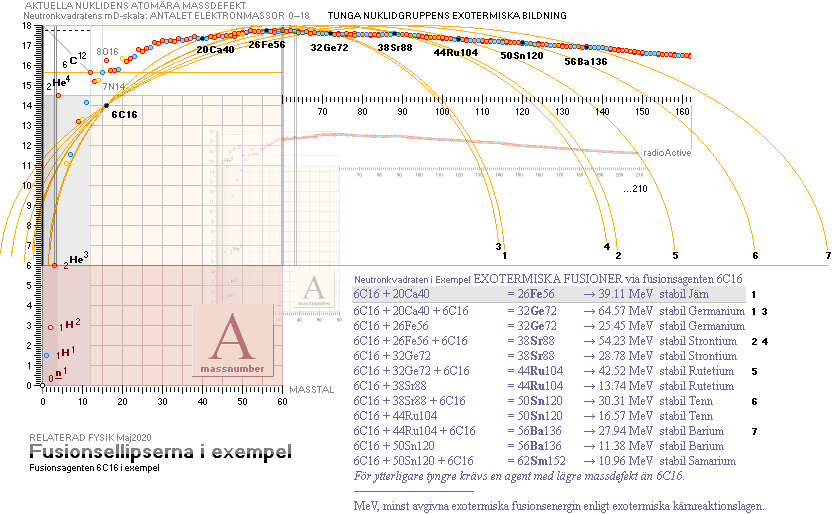
3Li8Nukliden: 6C16-grunderna
¦ 3Li6
GRUNDÄMNESBILDNINGEN I
RELATERAD FYSIK allmän genomgång i Neutronkvadraten
3Li8-nukliden kräver en del särskild uppmärksamhet:
3Li8
Tabell 1 A117 hExoterm2020test.ods

½NK-tvärellipsens egna mD-värden: 3Li8¦10.5860772
A
deuterium = Aref = 0.7305377 ¦ TNED
Varför intresset för 3Li8?
VI (med våra
kära husdjur): grundämnenas primärbildning enligt relaterad fysik.
Utvecklingen av den organiska kemin inom
Jordbiosfären.
Nuklidagenten 6C16 [(0.747S)→7N16(7.36S)→8O16] = 2×3Li8
spelar (möjligen, enligt TNED) en STOR roll i den möjliga kosmologiska (TNED)
förklaringen till grundämnesbildningen i Jordens himlakroppshistoria, såväl som
i fallet med alla övriga himlakroppar, säger TNED-kosmologin (Neutronkvadratens
exotermiska fusioner).
2He4 2He6 3Li8 4Be8
TNEDbasics
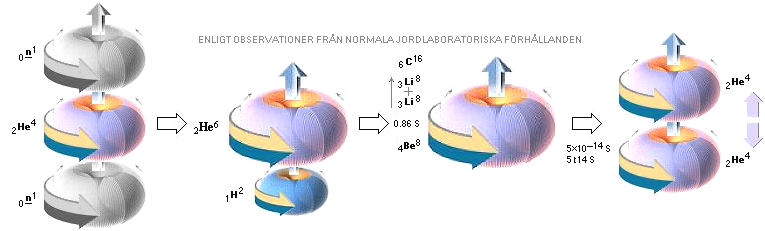
TNED ¦ KÄRNRADIERNA ¦ Kalkylkort EXOTERMISKA KÄRNREAKTIONSLAGEN
Exoterm2020.ods
minsta EXOTERMISKT AVGIVEN FUSIONSENERGI i MeV: n
+ 2He4 + n →¦0.96MeV¦2He6 + 1H2 →¦9.70MeV¦3Li8 + 3Li8
→¦27.96MeV¦6C16: sma 38.62MeV.
ENLIGT TNED i
NEUTRINOSPEKTRUM OCH PRIMÄRFUSIONERNA (se EXEMPLET ExoEx) är sönderfallstiderna
för betaaktiva nuklider (sådana med stora
neutronövervikter, typ 6C16) inte kritiska i den primära fusionsfasen:
de stora
frigjorda exotermiska elektronEkvivalenta fusionsenergier som genomtränger
himlakroppen under dess korta fusionsfas täcker gott och väl
excitationsgraderna i betasönderfallen; Dessa sönderfall börjar inte förrän
fusionsenergierna (neutrinostrålningens hf-värde) sjunker under hållvärdena för
aktuell betasönderfallande nuklid (energiekvivalenterna garanterar balansen).
DEUTERONENS HEMLIGHET ¦ NEUTRINOSPEKTRUM OCH PRIMÄRFUSIONERNA ENLIGT TNED ¦ EXEMPEL ExoEx
VERIFIERINGSTEST:
ovanstående 3Li8 resultat med hjälp av
ITERATIONSALGORITMEN
FÖR FUSIONSELLIPSERNA (se ITkort):
Det BORDE
finnas en
(originell, möjligen exotermisk, någonstans i området
0-14 minuter, neutronens normala sönderfall i Jordlaboratorier)
fusionsväg av
arten (med ledning av detaljerna ovan)
23Li8 →
6C16 → (7N16 → 8O16) + 6C16 → 14Si32 → 16S32
TVÅ snabbt förenade instabila 3Li8 till en instabil 6C16
som [0.747 + 7.36 = 8.107
S] får sönderfalla via kväve 7N16 [7.36 S ¦ VNS 5 1976 Table 3s495]
till en stabil 8O16 som förenas med en annan ännu 6C16 bildar en instabil
»JumboNeutronnuklidTyp» 14Si32 som så småningom slutar på en stabil
svavelatom:
enbart betasönderfall: Kisel 14Si32 till Fosfor15P32 på
700 år, därifrån på 14.22 dygn till stabilt Svavel 16S32].
I primärlokalens referens KAN sönderfallen 6C16 till
8O16 [halveringstid 8,107 S]
vara VÄL relevanta efter en initierande snabb primär fusionsfas vars
efterklanger [när fusionsenergierna ebbar ut från kroppen] kan realisera
sekundära mera normala sönderfall tillsammans med ev. kvarvarande [utflyende
via Coulombkrafterna] 6C16.
Det är i vilket fall de TNED-principiella exotermiska
möjligheterna.
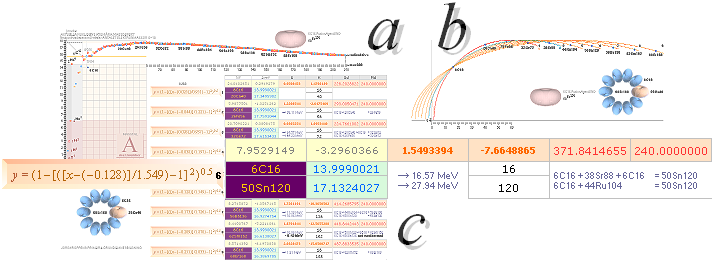
ITkort ¦ PRECISIONEN I ATOMVIKTERNA ENLIGT TNED
och SÅ baserad
på föregående fusionsbas för 3Li8 möjligen. Vi har dock ingen TNED-beräknad
atomär massdefekt för nukliden 6C16: Neutronkvadratens bascirkel antyder att
värdet skulle ligga nära 14 LBL-tabellens atomvikt (16.0147013) omräknad till
mD (=[1U/Amn]/me) ger värdet
mD(6C16)=13.9990021.
Insättning av
LBL-tabellens värden
mD1(3Li8)=10.5796723
och mD2(6C16)=13.9990021 i fusionsellipsens iterationsblock ger
K = 4.6150140
E = 0.7453747
;
Insättning av
TNED-mD-resultatet för 3Li8
mD1(3Li8)=10.5860722
och mD2(6C16)=13.9990021 i fusionsellipsens iterationsblock ger
K = 4.6009701
E = 0.7462942
;
3Li8Tabellerna: VERIFIERINGSTEST Nuk3Li8
Tabell 1 A124 hExoterm2020test.ods

ITkort ¦ PRECISIONEN I ATOMVIKTERNA ENLIGT TNED
Villkor: DifferensFaktor
För att
TNED-värdena ska vara meningsfulla i jämförelsen med experimentellt uppmätta
värden får jämförelsen TNED/Experimentell mellan största/minsta atomvikterna (U-värdena)
inte överstiga .......... 1.0008
och minsta/största
inte understiga
........ 0.999200639 = 1/1.0008
TNED-värdena
ska i inget enda fall göra våld på den gränsformen om det ska vara någon
mening med resultatbilden. Förekommer någon enda gränsöverskridning, är TNED
körd.
alternativa inslag ..

Genomgående
hittills i alla kontroller och jämförelser (2003+) har TNED-värdena via
Neutronkvadraten visat sig hålla måttet, inte sällan med (mycket) goda
marginaler som i dessa exempel.
Om
Neutronkvadraten (verkligen) håller vad den lovar, ska det inte finnas en enda
fysiskt möjlig exotermisk fusionsväg som INTE innefattas i neutronkvadratens
elliptiska funktionskomplex: alla fysikens exotermiska fusionsvägar ska vara
direkt illustrerbara via konkreta ellipsvägar. ÄVEN om vi amatörer kan ha
väldiga problem att hitta rätt: i princip varje fusionsväg måste göras 100%
relaterbar. I detalj.

½NK-tvärellipsens egna mD-värden: 3Li8¦10.5860772 6C16¦13.9998211 14Si32¦17.0602839
3Li8
VERIFIERINGSTESTETS AKTUELLA FUSIONSELLIPS[]
differenserna
(mellan de tre tabellversionerna) syns inte i denna skala:
3Li8 6C16 14Si32
![]()

NEUTRONKVADRATEN: Aref
= 6(1E) = max6 ¦ a0 = 60 √ 602 [5(mD 6)]2
= (A K)/E ¦ K = A a0E ¦
Hur ser en ellipslösning ut som beskriver
någon fusionsväg från lätta nuklidgruppen till den tunga den generella
bildningen av tyngre nuklider från Järntoppen och vidare mot max masstal (max
300 i TNED)?
Sätter vi enbart vår LIT till föregående ellipsITERATIVA exempel kan vi
hoppa över mellandelarna och gå direkt på en certifierad fusion för att få syn
på den aktuella fusionsellipsen som sammanknyter objekten.
Se exempel i
FUSIONSELLIPSERNA TILLSAMMANS.
noMASSorigin: Inledning ¦ Elaw
MASSAN Neutronen h=mcr=6.626 t34 JS
SAKNAR UPPHOV DÄRFÖR ATT ENERGIN GÖR
DET
Det går inte
är logiskt, intrinsiskt, omöjligt att relatera ett yttersta upphov
till massans
existens på energilagens kredit: energi kan varken skapas eller förintas,
endast omfördelas.
Upphov saknas.
GRUNDÄMNESBILDNINGEN GENOM FUSIONSPROCESSERNA I DE
PRIMÄRA HIMLAKROPPARNA
enligt relaterad fysik TNED
Så formulerar energilagen
sig själv i formen av en Kosmisk Allmän Tillståndslag som gäller för den
pulserande centrala K-cellen inom energilagens »massa saknar upphov: får
förstås obegränsat»:
En DETONATIONSFAS (konv. BigBang)
inträder vid varje kontraktionsmaximum;
Kontraktionsmaximum ljusfysikens
g-beroende tvingar all kontrakterad massa att NEUTRONFRAGMENTERA: alla tidigare
bildade atomkärnors sammansättningar löser upp sig i form av återbildade
neutroner (massformen är känd i modern akademi som sådan och kallas
konventionellt för typen neutronstjärna):
NolldivergensZonen ¦ Dmax ¦ K-cellens expansion ¦ Galaxbildningen ¦ Solsystemen
i Vintergatan ¦ DIAKVADRATEN
nuklidbildningarna
Detonationen kastar ut den universellt komprimerade
neutronmasskroppen (K-cellen primärt) i formen av uppdelningar
likt vattenfysikens vattendroppsuppdelningar som kan studeras i detalj.
Ljusfysikens gravitella beroende ser till
att allt neutronsönderfall (normalt 12-14 minuter) är i läge OFF så
länge gravitationen framtvingar noll makroskopisk ljushastighet;
En DIVERGENSZON Nolldivergenszonen
gränslinjen mellan c=0 och c>0 sveper fram över den
detonerade K-cellen med konstant ljushastighet (c=c0) genom
hela Expansionsfasen;
Divergenszonen tänder neutronsönderfallet
för varje berörd särskild utkastad avdelad neutronkropp.
Neutronsönderfallet
resulterar i en fusionsfas med en efterföljande expansionsfas där himlakroppens
mineralogi utformas slutligt.
Se särskilda avsnitt som
berör TNED-kosmologins beskrivning av himlakroppsbildningens mineralogiska
detaljer i JÄRNKÄRNAN
och IsBILDEN.
Vi studerar en
översikt som visar DIFFERENSER MELLAN
MODERN AKADEMI OCH RELATERAD FYSIK
ATOMVIKTERNA FRÅN ATOMÄRA
MASSDEFEKTER
Vi kan studera jämförande
skillnader och differenser mellan TNED och MAC (modern akademisk
kärnfysikalisk teori via Weizsäckersambanden) genom jämförelser
EXPERIMENTELLT/TNED kontra EXPERIMENTELLT/MAC. Jämförelserna här innefattar
enbart stabila nuklider, dvs., alla atomfamiljer ZatomA från 0n1 till
83Bi209:
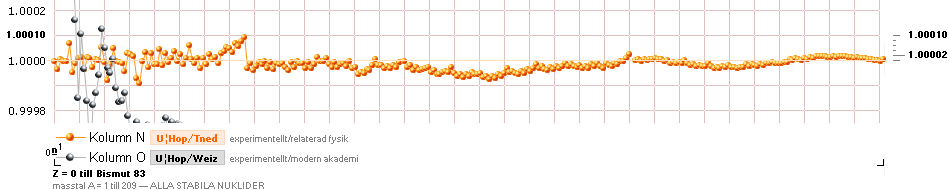
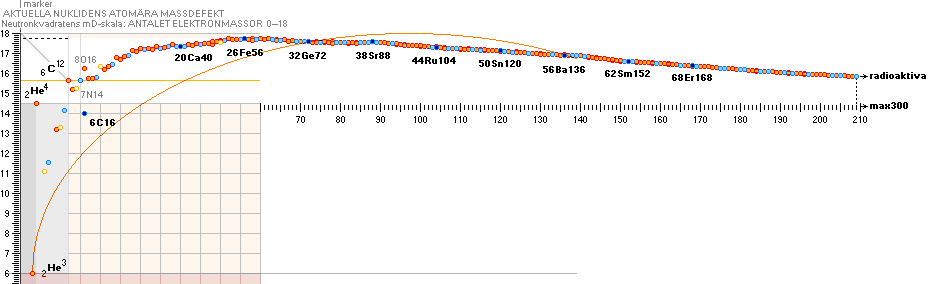
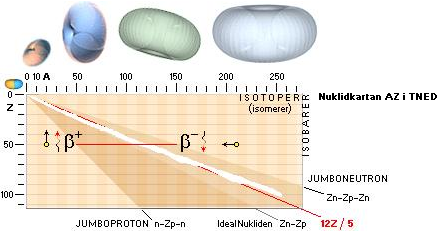
StabDiff: DiffGraf
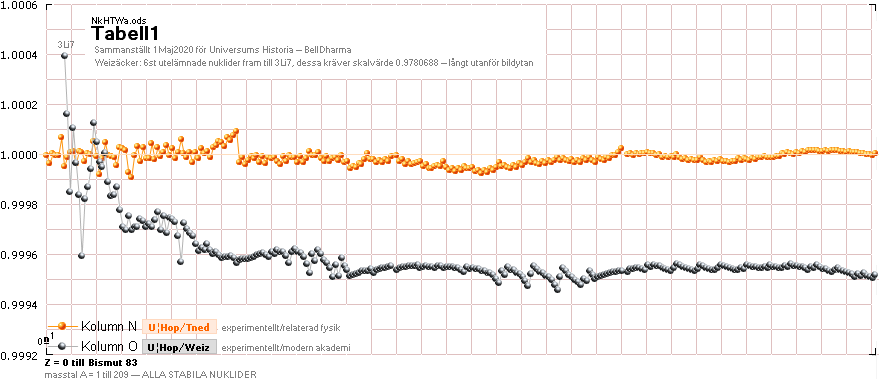
DIFFERENSERNA
Experimentellt/TNED är som vi ser nära försvinnande små.
Experimentellt/ModernAkademi däremot uppvisar trots »allmän följsamhet» men med
vissa kaotiska inslag, speciellt i början. Det har klassificerats från ruta ett
i Universums Historia som »ren utklassning».
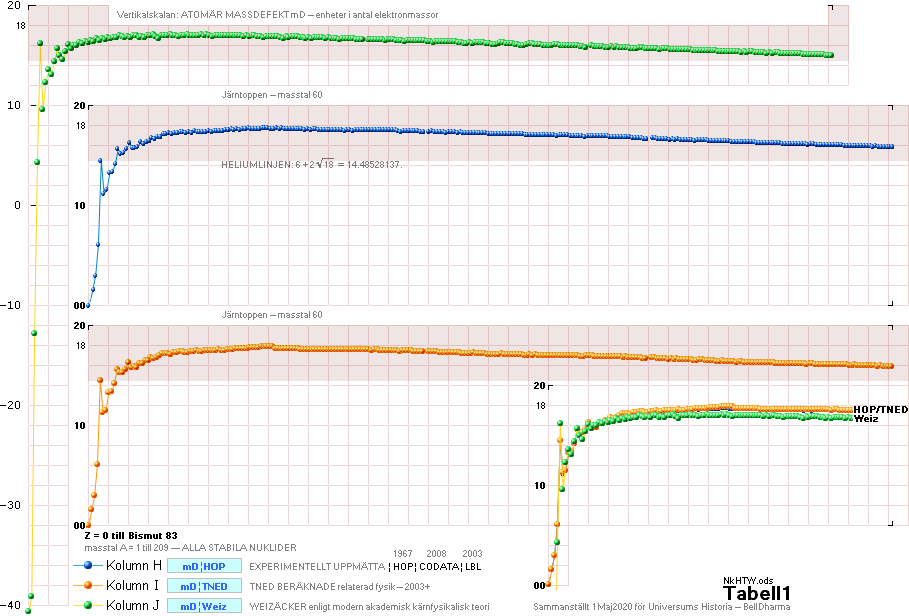
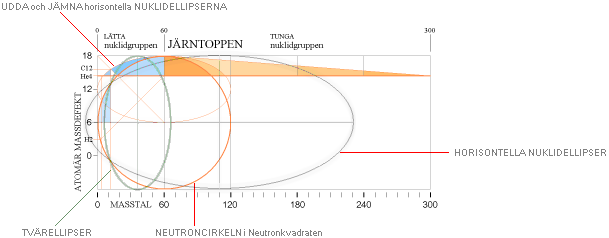
Det lilla TNED-hacket ![]() i övergången mellan lätta-tunga nuklidgrupperna
berör gränsfallet mellan ellipsfunktionen och hyperbelfunktionen.
Neutronkvadratens idealt fast geometriska mönster-A=60-gräns är emellertid inte
fullt i överensstämmelse med den praktiska kärnfysikens mera mobila
nuklidindivider: det finns en viss övergångsosäkerhet i området masstalen 58
till 60 (Järn-Kobolt-Nickel). Används även hyperbelsambandet för den delen (i
stället för strikt från masstal 60+) försvinner hacket och värdena harmonierar
mera direkt med de övriga HOP¦CODATA¦LBL experimentellt uppmätta [Blå graf].
De två öppningarna i blågrafen beror på att två av förekomsterna efter
atomnummer inte är stabila [43Teknetium och 61Prometrium].
i övergången mellan lätta-tunga nuklidgrupperna
berör gränsfallet mellan ellipsfunktionen och hyperbelfunktionen.
Neutronkvadratens idealt fast geometriska mönster-A=60-gräns är emellertid inte
fullt i överensstämmelse med den praktiska kärnfysikens mera mobila
nuklidindivider: det finns en viss övergångsosäkerhet i området masstalen 58
till 60 (Järn-Kobolt-Nickel). Används även hyperbelsambandet för den delen (i
stället för strikt från masstal 60+) försvinner hacket och värdena harmonierar
mera direkt med de övriga HOP¦CODATA¦LBL experimentellt uppmätta [Blå graf].
De två öppningarna i blågrafen beror på att två av förekomsterna efter
atomnummer inte är stabila [43Teknetium och 61Prometrium].
![]() :
:
Dessa är beräknade genom
1. sammanställningarna i lätta nuklidgruppens resultat (se MASSDEFEKTSEKVATIONEN
2003) masstalen A=1till60 och 2. tunga nuklidgruppens resultatvärdet från mD¦HRBwave
resterande till A=209.
MASSDEFEKTSEKVATIONEN
2003 ¦ mD¦HRBwave-ekvationerna ¦ WeizsäckerEkvationen ¦ Hofstadters
spridningsexperiment 1961 ¦
Jämförelserna visar
alldeles tydligt att experimentalfysiken + TNED relaterad = härledd
kärnfysik = sant.
Särsklilt i början från
0n1: De allra första nukliderna där den moderna akademins generellt
antagna vattendroppsmodell för atomkärnan ställer till med gruvliga
konventionsbrott i fysiken. Se även jämförande data i KÄRNRADIERNA II (Hofstadters
elektronspridningsexperiment som gav viss vägledning, men som numera har
förkastats och ersatta av andra mera Avancerade Laserbetonade Modernt
DatorModellerande Begrepp).
U¦eDIFF: eDIFFen
DIFFERENSERNA i ANTAL
elektronmassor U¦(TNEDHOP)/me:
från originalarbeten 2003 i MsWORKS 4.0 som plötsligt förbjöds/stängdes för
av Microsoft i Windows Vista 2008:
Vertikalskalan med massdefektsdifferenserna i antal
elektronmassor 0.000548598u:
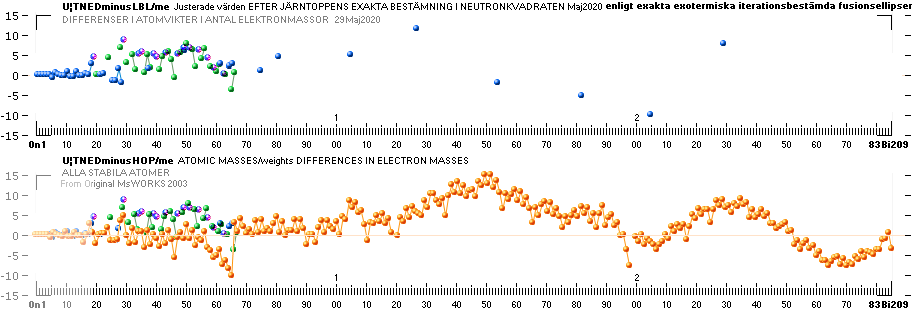
Undre orangea Efter originalarbetena 2003:
Neutronkvadratens atomviktsvärden minus de experimentellt uppmätta
(HOP-tabellen) i antal elektronmassor visar precisionen. Differenserna fram
till 3Li6 (No5; 0.76) är helt försumbara: Dessa kopplar helt blygsamma
kvantiteter för massökningseffekter från accelerationsspänningar i
storleksordningen 10 KV. Övre blå: Precisionsbestämda neutronkvadratsvärden via
exotermiskt fusionsbestämda iterationsellipser efter Järntoppens
mD-NK-bestämning. Se IronTop 26Fe56. Den delen står här i skrivande stund under
fortsatt löpande framställning (iterationerna är delvis besvärliga, och det tar
tid att få fram resultaten jämför Kurvskaran för 6C16).
NOTERING/ARGUMENT differenser
i ett mindre antal elektronmassor:
Enda direkta skillnaden
som kan finnas mellan Neutronkvadratens motsvarande mD-atomviktsvärden
(U)
U = Amn(1
mDme)
och de experimentellt
uppmätta (HOP, CODATA, LBL, alla med
försumbara inre differenser) ligger uteslutande i den möjliga differens
i elektronmassa som den masspektroskopiska atomen måste joniseras genom.
Massobjektet atomen måste elektrifieras avlägsnas (eller påföras) lägst en
elektronladdning för att den ska få hastighet i en partikelaccelerator och så
kunna uppmätas i spektrografens avläkningsanordning.
Skillnaden i massa mellan
den joniserade och neutrala atomen har bara motsvarande elektronmassor att
återfalla på.
DET FINNS INGEN ANNAN MASSFORM ATT RÄKNA PÅ UTÖVER
ATOMKÄRNANS MASSA ÄN ELEKTRONMASSAN
Ingen annan
massform finns att välja på.
DET ENDA TILLGÄNGLIGA ATT
SUBTRAHERA ÄR DEN BROMSANDE ATTRAKTIONSKRAFT SOM DE AVLÄGSNADE
MODERELEKTRONERNA UTÖVAR PÅ MODERKÄRNAN I DET ATT DEN ACCELERERAS GENOM
SPEKTROMETERANORDNINGEN: i tröghetshänseendet praktiskt taget försumbart:
några få avlägsnade elektronmassor på en accelererad typ Järnkärna har ingen
direkt inverkan. Snarare omvändningen: moderkärnan utövar den större dragverkan
genom sin större masströghet mot de lättare elektronmassornas ringa (helt
försumbara) tröghetsmotstånd..
Masspektrografens
princip
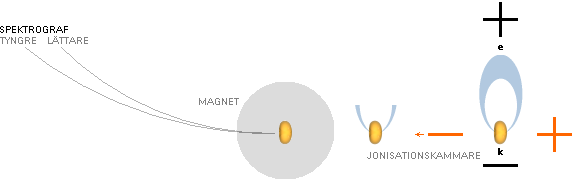
Neutrala atomer berövas först eller erhåller extra
någon del av sin elektronbesättning: atomkärnan joniseras i en
jonisationskammare. Jonisationsprocessen blottlägger den positivt laddade
atomkärnan. Den blottlagda kärnan attraheras av en rätvinkligt ställd elektrisk
accelerationsanordning. Om kärnan passerar fältet mellan ett par lämpligt
utformade magneter, avlänkas kärnan olika mycket beroende på dess massa. En
spektroskopisk skärm fångar upp spåren efter atomerna sedan de avlänkats.
Beräkningsalgoritmer används sedan för att få fram aktuell atommassa.
Eftersom Neutrokvadraten beskriver neutrala atomer
idealt vilande helt opåverkade uppkommer en intressant frågeställning.
Nämligen i observationen att differensen i atomvikt uttryckt i antal
elektronmassor mellan Neutronkvadratens värden och de experimentellt uppmäta
gängse tabellverk (HOP CODATA LBL) just skiljer i intervallet grovt 0-10. De
första grundnukliderna avviker helt obetydligt. Differenserna märks först från
3Li6 (0.76).
KinaLedets ekvation och framställning visar och bevisar
att det redan finns ett mindre märkbart massfel i kalkyleringen
(ENERGILAGEN och MASSBEGREPPET) lägst obetydliga 0.0000283 för 1H1 och störst
mera märkbara (LBL-tabellen) för 118Ui293 med 2.8982892. Utöver den uppgiften
finns inget ytterligare känt om den exakta räkneprocedur som används i den
masspektroskopiska sluträkningen för de olika atomernas massor. Vi måste få se
den räkningen i detalj, innan något vidare kan fastställas.
ENERGILAGEN
och MASSBEGREPPET ¦ KinaLedet ¦ NEUTRONKVADRATEN
Inga närmare kvantitativa
besked finns på de avgörande punkterna från etablerat håll, eller ens hur man
räknar/skriver sambanden i detalj utom möjligen typen (KinaLedet)
Nowadays several
measurements are conducted with fully or
almost fully ionized atoms. In such cases, a correction muste be made
for the total binding energy of all the
removed electrons Be(Z),.
CHINESE
PHYSICS C Vol. 41 ¦ eDIFFen
MODERN
AKADEMI:
massa + massa massa = ENERGI = massa
MN
(A,Z) + Z×Me MA
(A,Z) = Be(Z) ;
RELATERAD
FYSIK:
massa + massa massa = massa ≠
energi : bindningsenergi är
inte vägande massa.
ENERGILAGEN
och MASSBEGREPPET ¦ KinaLedet
Total binding energy
kopplar ingen massform.
Den spektroskopiska
atomen dras upp till hastighet utan sin normalt tillhörande yttre
elektronbesättning, och uppträder därför som en något lättare komponent (massökningseffekter
i jämförande kvantitet är i dessa sammanhang helt försumbara, se eDIFF.en).
Positiva värden i grafbilderna ovan antyder den typen, medan negativa antyder
ett tillskott.
Men det finns här ännu inga motsvarande
etablerade uppgifter att gå på för jämförelsen:
CHEMISTRY LIBRE TEXTS,
2016 ¦ 4.1: Atomic Mass
Because atoms are much too
small to measure individually and do not have charges, there is no convenient
way to accurately measure absolute atomic masses. Scientists can measure
relative atomic masses very accurately, however, using an instrument called a
mass spectrometer.,
The technique is conceptually similar to the
one Thomson used to determine the mass-to-charge ratio of the electron. First
electrons are removed from or added to atoms or molecules, thus producing charged
particles called ions. When an electric field is applied, the ions are
accelerated into a separate chamber where they are deflected from their initial
trajectory by a magnetic field, like the electrons in Thomsons experiment..
Gängse litteratur
hittills beskriver enbart mera övergripande spektroskopiska aspekter.
Webben blir
också allt svårare att konsultera
(Apr¦Sep¦Nov2020): En del naturvetenskapliga webbsidor har börjat stänga till
helt och hållet för insyn om man inte accepterar anslutning till COOKIES.
4Nov2020: Google&Microsoft låser alla internetsidor om man
inte medverkar i cookies.
Planeten är fortfarande
rund: alla människor har samma grundläggande rättigheter, och kunskapen är
öppen för alla 24/7 utan åtskillnad. Det finns ingen som helst anledning att
utestänga, hindra, uppehålla eller på annat sätt märka upp någon enda människa.
Typer som ändå gör det, hittar på anledningar för att bryta sig in, skapa
avbrott i den individuella människans kunskaps- och associationsflöde, sätta
fram hinder, framhäva eget, introducera avbrott, gör bäst i att göra det
tydligt och synligt. Vi återkommer till dessa särskilt senare.
AVGÖRANDE FRÅGA: En och
samma ZnamnA familjens atomindivider med marginellt olika
atomvikt = olika atommassa?
KAN OLIKA mD-VÄRDEN=ATOMVIKTER FÖR EN OCH SAMMA ZnamnA
FINNAS? Naa ..
ZnamnA normal
associerat EN BESTÄMD ATOMVIKT
EN OCH SAMMA ATOMNUKLID ZnamnA
kan ha (något, litet marginellt) olika U beroende på exotermiska fusionsvägen?
Vi har hittat en
kandidat (29Maj2020):
8O17(1)mD=15.751656¦ Tvärellipsbestämd med 2He6; ......... (U¦TNEDU¦LBL)/me
................................................ = 0.1058702244
8O17(1)mD=15.75179575¦ Tvärellipsbestämd med 2He6; ........... (U¦TNED16.9990736U¦HOP16.9991329)/me
......... = 0.1080963722
8O17 = 1H1 + 1H2 = 2He3 ¦ + 2He6 = 4Be9 ¦ + 3Li6 = 7N15 ¦ + 1H2 = 8O17
8O17 = : ALLA EXOTERMISKA minMev:
6.30 ¦ 43.94 ¦ 23.64 ¦ 8.78 ¦ : 27.61 ¦ 55.18 ¦ 18.11 ¦ 5.40 ;
2He4 + 6C13 = 8O17 ¦ + [2·7N15 = 14Si30] = 22Ti47 ¦ + 3Li6 =
25Mn53 ¦ + 1H1 = 26Fe54 ¦ : 22Ti47 ¦ + [3Li7+1H3 = 4Be10] = 26Fe57
¦ : 26Fe54 + 2·6C16 = 38Sr86 ¦ + 6C16 = 44Ru102 ¦ + 6C14 =
50Sn116
8O17(2)mD=15.7207076¦Horisellipsbesmd
med 2He4; ..................... (U¦TNEDU¦LBL)/me
............................................... =
+0.5328666214
ref. N160 Exoterm2020test.ods:

50Sn116 avviker med +14e
i atomviktsdifferenserna vilket möjligen gör hela den mD-uppgiften tveksam.
Tabell 1 N160 hExoterm2020test.ods

Det kan ju också vara så att »den som gäller» är den
med minsta massförlusterna = mest stabila anordningen. Vi hittar (nämligen,
ibland något) olika e-differensvärden för redan tidigare bestämda genom de
olika möjliga ellipsvägarna. Som i detta fall, samma parametrar som ovan,
Järntoppen 26Fe56
![]()
som här tydligen avviker mera märkbart från den tidigare
bestämda via mD-värdena för 6C16 och
20Ca40 ;
mD(26Fe56) = 17.7098627; eDIFF = 2.7814300.
8O17 i det första fallet är dessutom bestämd via en
grundTvärEllips och borde enbart av den anledningen utöver mest tajta
passningen representera det genuina mD-värdet. Vi antar fortsättningsvis den
ordningen, om inget annat anges.
JärnToppen ¦ 8O17 ¦ 1818
+ 18 + k
8O17(0)mD=15.7517834¦LBL-tabellvärdet;
Skillnaden mellan de
bägges atomvikter
(1) 16.9990736
(2) 16.9994240
= 0.000312u
skulle (här veterligt)
vara helt omöjlig att avgöra genom en masspektrometerAnordning. Nämligen i
begreppet SPRIDNING kanske t.o.m. beroende på lokal och region: färre eller
flera; »Man hittade olika Typer beroende på var man Letade». Bidra gärna med
klargörande den som kan.
I PRINCIP: VARI skulle
masskillnaden bestå? HELA atommassan skiljer här i vårt uppmärksammade exempel
på 0.63 elektronmassor (gott och väl inom k-värdet i antalet 1818+18+k
elektronmassor i neutronen). I varje fall i TNED-teorin finns ingen
möjlighet att utesluta den variationen (alla inom k grovt max 2.6
elektronmassor [per neutron]).
Olika fusionsvägar
och därmed olika fusionsgradienter (ellipsbågarna), häftigheten i
exotermiska föreningen bestämmer slutformen.
Men det finns också en annan (»mera
kraftig») aspekt, som ovan:
Minsta möjliga
motståndets lag ombesörjer mesta möjliga hushållning på minsta möjliga arbete.
Om det finns två vägar med två olika mängder, väljer Naturen alltid den som tar
minst tid, kräver minst arbete och utförs snabbast: maximal skärpa.
Lägsta differenserna mot noll. Alltid.
FEalla: 6C16-agenten
Bilden klarnar ..
identifieringsfallen ..
DEN GENERELLA
BEVISBARHETEN
FUSIONSELLIPSERNA I LÄTTA OCH TUNGA NUKLIDGRUPPERNA
TILLSAMMANS
Ännu (Apr2020):
KÄRNREAKTIONSLAGEN
certifierar en viss fusionsprodukt:
Vi finner också dess
motsvarande fusionsellips via enbart agent och produkt.
Men då enbart i
tabellvärdenas referens som bevisar att en koppling existerar inom vissa
mindre toleransgränser. För att få ut agent, objekt och produkt, alla tre i
samma fusionsellips och i mix mellan lätta och tunga grupperna, krävs en mera
omständlig procedur. Se inledningsexemplet med 54Xe130.
INLEDNINGSEXEMPEL
fusionsellips i lätta och tunga gruppen; 54Xe130 ¦
¦ Kalkylkort EXOTERMISKA KÄRNREAKTIONSLAGEN Exoterm2020.ods
Hur finner vi
FusionsEllipsen till fusionskomponenterna Agent→Produkt om vi känner
Agent→Objekt?
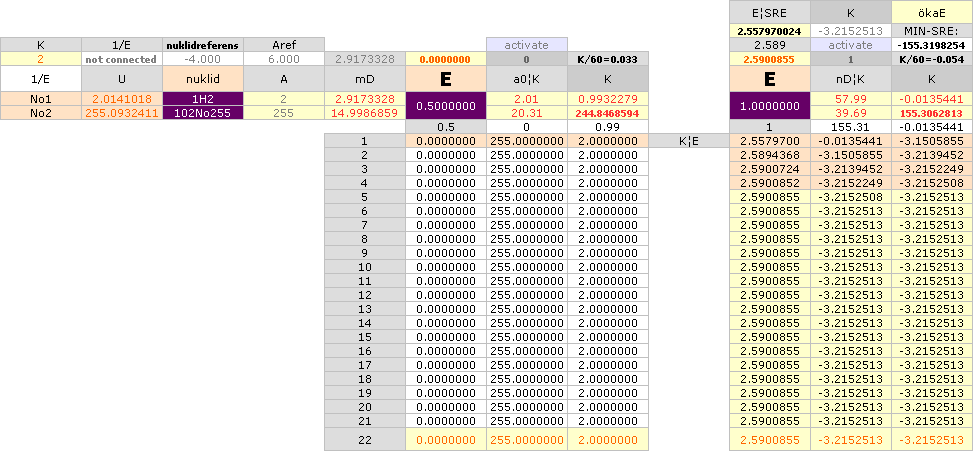
(TYP: 1H2 + 102No255 =
103Lr257)
SVAR (Maj2020 efter många olika vidare
utvecklingsdetaljer):
GENERELLT MELLAN LÄTTA
OCH TUNGA NUKLIDGRUPPERNA:
För att få fram alla tre
skärande en och samma ellipsbåge är vi allra först hänvisade till en exotermisk
fusionsanalys: Vi måste veta fusionsordningen, exakt, mellan komponenterna
agent-objekt-produkt, och säkert veta att fusionen verkligen är exotermisk =
ger ut energi vid fusionen.
För att få fram endast
två av de tre förutsatt exotermiskt fusionskontrollerad via exotermiska
kärnreaktionslagen räcker det med att mata in komponenterna agent-objekt
eller agent-produkt i ellipsiterationsalgoritmen (kalkylkort). Se ENKLA
FUSIONSELLIPSERNA.
ENKLA
FUSIONSiterationsELLIPSERNA ¦
Kalkylkortet tar fram den
ellipsen och dess parametrar omgående. Vi kan alltid testa den delen med
hjälp av diagrampunkter över experimentellt uppmätta atomvikter (U) med
motsvarande omräknade atomära massdefektsvärden mD=(1U/Amn)/me genom att
se efter att aktuella nuklidobjekt verkligen skärs av ellipsbågen (inget
hittills påträffat fall som har missat den delen om det sker går jag hem).
Prövning på sambandsformerna i den härledda exotermiska
kärnreaktionslagen garanterar alltid överensstämmelsen.
För att få fram alla tre
produktens atomära massdefektsvärde beräknas oberoende genom de redan kända
Neutronkvadratsvärdena för agent och objekt kan den enkla ellipsbågen mellan
två komponenter användas som en första ansats (parametervärdena K Sd och Md).
Fortsättningen kräver nämligen en högre (betydligt mera krävande)
iterationsnivå. Exempel på sådana ges här längre fram. Se från BELYSANDE
PRECISIONSEXEMPEL med 26Fe56.
Belysande
precisionsexempel ¦ Kalkylkort EXOTERMISKA KÄRNREAKTIONSLAGEN
Exoterm2020.ods ¦
mD ORIGINALVÄRDENAS
BESTÄMNING från grundarbetena 2003 ¦ Utvecklat 2020
Tidigare enda fristående sambandsformen för fallen med
nukliderna 60+ var den allmänna Hyperbelformen (mDHRB¦wave) som i sig
tämligen väl ansluter till experimentellt uppmätta STABILA nuklider alltså
fram till Bismut (sv. Vismut: Bi atomnummer 83 masstal 209 med en del vidare
..).
Se särskilt i DEN TUNGA NUKLIDGRUPPENS CERTIFIERING: exotermiska
exempelräkningarna som bevisar fusionerna upp till de allra tyngsta nukliderna.
TUNGA NUKLIDGRUPPENS CERTIFIERING ¦
I samtliga fall
verifieras beräkningarna via allmänna atomära massdefektsekvationen.
Den gäller också
enhetligt för samtliga fall (CEPH-ekvationen):
SMÅ »ovidkommande skillnader» framträder i
atomvikterna mellan HRB och HRBwave.
Mera allmänna precisa bestämningsfall även för den
tunga nuklidgruppens atomindivider ges från
Fusionsexempel, Lätta-Tunga: Inledande Exempel
FUSIONSAGENT + FUSIONSobjekt
ENKLA ELLIPSITERATIONEN
illustrerat nedan i exempel kan ringa in två eller flera sant
exotermiska fusionskomponenter (som först har kontrollerats exotermiskt,
se Exotermiska Kärnreaktionslagen). Däremot krävs en ytterligare
djupdykning (minst tre komponenter: agent, objekt och produkt) för att
kunna definiera Neutronkvadratens motsvarande egna atomära massdefektsvärde (mD)
för produkten: mD-värdena för både agent och objekt måste obönhörligt vara
bestämda via neutronkvadraten för att också kunna bestämma produktens
neutronkvadratsrelaterade mD-värde.
Se särskilt sammansatt
exempel från 2He4 till 54Xe130.
Enkla
ELLIPSITERATIONEN ¦ Kalkylkort EXOTERMISKA KÄRNREAKTIONSLAGEN
Exoterm2020.ods ¦ Ex2He4TILL54Xe130
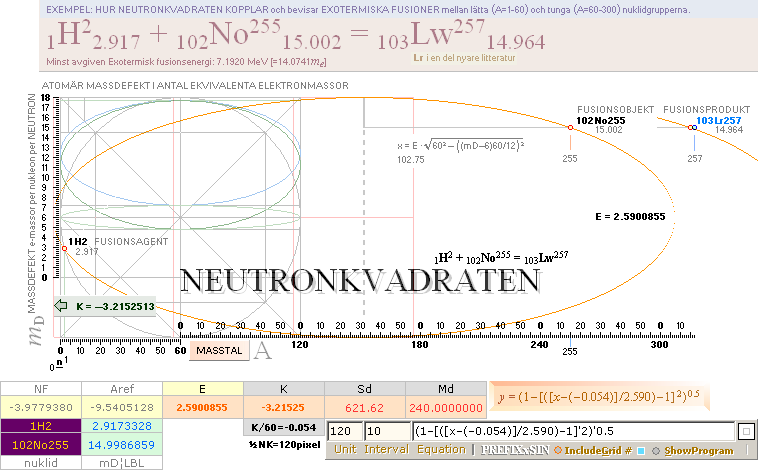
FUSIONSAGENT + FUSIONSprodukt
Neutronkvadratens
fusionsellipser visar att vi ALLTID genom tabellerna för redan uppmätta
atomvikter, här den omfattande LBL-tabellen (direkt) kan ringa in (minst) två
fusionskomponenter (tabellexakt). Vi kan sedan använda den
![]()
ellipsen som grund för en
vidare utvärdering men
ytterligare, mera komplicerade iterationer krävs för att få fram
Neutronkvadratens motsvarande egna oberoende massdefektsvärden, och därmed
atomvikter till jämförelse.
Se utförligt från
BELYSANDE PRECISIONSEXEMPEL.
Belysande
Precisions Exempel ¦ Jämförande
diagram CODATA/HOP
ELLIPSANALYSEN NEDAN/ovan IN TILL TUNGA NUKLIDGRUPPEN
FANNS INTE TIDIGARE
utvecklades först här
med början (Mars-April) 2020 för
ökad beviskraft i relaterad atom- och kärnfysik
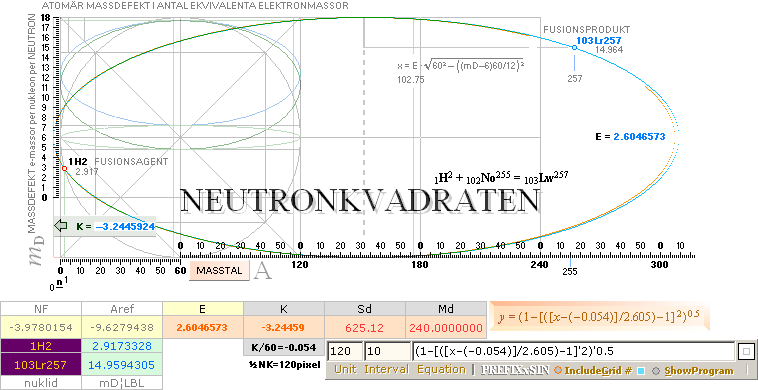
x60/K = +0.054 ellipsens placering utmed x-axeln.
2020V7
FUSIONSELLIPSERNA AV PRINCIP
MASSDEFEKSEKVATIONEN mD
= a + bE√cx x2 från CEPH-ekvationen offsetvärde (a)
gäller av princip vilka
som helst horisontella och vertikala ellipser inom NEUTRONKVADRATEN: begränsningar
saknas.
MASSDEFEKTSEKVATIONEN
2003 ¦ Ellipsfunktionen ¦ CEPH-ekvationen ¦ NEUTRONKVADRATEN
Tabell 1 O34 hExoterm2020.ods
ITERATIONSDELEN TILL FUSIONSELLIPSERNA
Fusionsellipserna
Värdena som kommer fram 1/E och K
matas in (manuellt) i grafprogrammets ellipsekvation som sedan (Enter) ritar ut
aktuell ellips för analys och illustration.
TVÅ GODTYCKLIGT GIVNA PUNKTER i xy-planet
kan alltid beröras/genomskäras av en CIRKELBÅGE;
BEVIS: Cirkelns radie,
diameter eller korda förenar/definierar alltid två godtyckliga punkter
°
°
TRE GODTYCKLIGT GIVNA PUNKTER i xy-planet
kan alltid beröras/genomskäras av en ELLIPSBÅGE, i en del fall även av en
cirkel, men inte alltid.
BEVIS: Punkterna med
största avståndet = Ellipsens storaxel (Md major axis): tredje
punkten väljs alltid så att den projiceras som normal (rätvinkligt) på
(Md):
°
°
°
Genom att öka ellipsens
lillaxel (Sd, semi axis) skär så ellipsbågen den tredje punkten.
En cirkelbåge kan inte
alltid fånga in en så definierad tredje punkt.
MED NUKLIDSYSTEMETS atomära
massdefekter och dess alla ORGANISERADE xy-PUNKTER i xy-planet
nuklidernas aktuella
atomära massdefektsvärden
över/under TVÅ
HORISONTELLT () BESTÄMDA ELLIPSÄNDAR
KAN ALLA MÖJLIGA minst
TRE SYSTEMPUNKTER SKÄRAS AV EN LÄMPLIG ELLIPSBÅGE.
Neutroncirkeln i Neutronkvadraten ¦ UDDA och JÄMNA horisontella
NUKLIDELLIPSERNA
TVÄRELLIPSERNA ¦ Horisontella
nuklidellipsena
I Neutronkvadratens fall
bestäms ellipsbågens skärning med givna nukliders atomära massdefektsvärden
uteslutande enbart av
EXOTERMISKA
FUSIONSVILLKOR.
Begränsningar
NEUTRONKVADRATEN ÄR EN STATISK GEOMETRISK ANORDNING
idealt fasta neutrala icke joniserade gitteratomer
Nuklidreferenserna i
Neutronkvadraten utgår ifrån EXOTERMISKA FUSIONSORDNINGAR: Dessa föreligger
bara uteslutande endast enligt TNED i himlakropparnas primära bildningsfaser med
utgångspunkt från ett maximalt tätt materietillståmd (ATOMKÄRNANS
INKOMPRESSIBILITET): Neutronmassorna. Genom att neutronerna redan ligger
innanför varandras kommande nuklidbarriärer som sönderfallna väteatomer
protonkärnorna behövs inga yttre moment för att igångsätta exotermiska fusionsprocesser.
Atomkärnans inkompressibilitet ¦ Kalkylkort EXOTERMISKA
KÄRNREAKTIONSLAGEN Exoterm2020.ods ¦
VILKA MÖJLIGA KÄLLOR FINNS FÖR AVVIKELSER MELLAN
NEUTRONKVADRATENS VÄRDEN OCH MOTSVARANDE EXPERIMENTELLT UPPMÄTTA?
Enda här ännu kända
svaret:
Antalet elektronmassor som varje (masspektroskopiskt)
mätande utrustning måste påföra atomobjekten genom jonisationsprocesser för att
få atomobjekten att flytta sig in till anordningens mätande sensorer.
Om Neutronkvadratens
värden är av typen »väl balanserade» bör avvikelsen mot experimentella värdena
ligga i storleksordningen (beroende på atomobjekt) 2-10 elektronmassor. Se
diagrammet U¦eDIFF. Direkta uppgifter från experimentella uppmätningar på den
parametern saknas här (olika atomobjekt kräver olika typer av
jonisationsanordningar, tillgång till direkta laboratoriedata krävs).
Massökningseffekter
(eDIFFen) i mätförloppen har i dessa sammanhang (enkla räkneexempel) praktiskt
taget ingen inverkan. De är alltför blygsamma för att spela någon roll.
Maxvärdet 18 (Se
1818-kroppen) för atomära massdefekterna är ett absolut idealt toppvärde som
aldrig uppnås i praktiken: Praktiska toppvärdet innehas av den experimentellt
uppmätta (Järntoppen) stabila järnnukliden 26Fe56 med värdet 17.759142
~ 17.76.
DIFFERENSERNA MÄRKS TYDLIGAST I
ORDNINGEN FÖR DEN SÅ KALLADE JÄRNTOPPEN: nuklidkartans morfologi:
ORDNINGEN OVAN UNDERST refereras också i PDF-dokumentet
CHINESE PHYSICS C Vol. 41, No. 3 (2017) 030003 The
AME2016 atomic mass evaluation, s30003-3sp1ö:
The highest
binding energy per nucleon is observed for 62Ni, followed sequentially by
58Fe and
56Fe..
Neutronkvadratens eget
värde (se Järntoppen: 26Fe56¦17.7098627: U¦eDIFF=2.7814300) bestämmer
18-skalans absolut högsta fysiskt möjliga toppvärde. Det värdet kan (nu
Maj2020) utnyttjas för att undersöka/avstämma eventuellt högre noggrannheter i
de tidigare (2003) beräkningarna (udda-jämna-basellipserna) där nuvarande
utvikningar ännu inte var bekanta.
JÄMFÖRELSER villkor:
Vi utnyttjar redan
experimentellt uppmätta atomvikten
(U, som beräknas från
atomära massdefekten: mD = [1 U/Amn]me;
A masstalet, mn U-neutronmassan 1,0086652, me U-elektronmassan 0,000548598)
som referensindex i
samtliga utan undantag prövningar, analyser och utvärderingar i bevisen:
och undersöker sedan hur och på
vilket sätt som Neutronkvadraten DEFINIERAR dessa atomvikter (atomära
massdefekterna mD) av princip
genom de Elliptiska funktionerna och deras
ekvationer om alls.
Någon annan referens är inte här känd.
Grundämnesbildningen, dess mera
detaljerade sidor:
HUR GRUNDÄMNESATOMERNA BYGGS UPP MED BÖRJAN FRÅN
NEUTRONERNA I RELATERAD FYSIK
NEUTRONKVADRATENS
GEOMETRISKA-FYSIKALISKA FUSIONSMORFOLOGI
NEUTRONKVADRATENS exotermiska fusionsMORFOLOGISKA
MÖNSTERKROPP
Tyngre nuklider i den lätta nuklidgruppen (1-max60)
»fusionspumpas» genom de allra lättaste grundnukliderna med givna egna
mD-värden direkt givna från Neutronkvadratens geometri. Se GRUNDNUKLIDERNA.
De tyngre produkterna definieras så på de lättares atomära massdefekter.
För att komma in i tunga nuklidgruppen, masstalen 60+,
finns särskilda fusionsagenter i den lätta gruppen som fortsätter »pumpa in»
exotermiska nya produkter in till den tunga gruppen. Se särskild
inledningsexemplet med 54Xe130-serien. Samt vidare i KURVSKARAN för 6C16-agenten.
Vartefter den tunga nuklidgruppen avancerar med allt
tyngre gränsen enligt TNED går vid Amax = 300 (eg. 317, se NUKLIDKARTANS
GRÄNSVÄRDE) krävs fusionsagenter i den lätta gruppen med allt lägre egna
atomära massdefekter: tyngre »fusionspumpas» utåt högeränden genom användning
av lättare alltmer mot vänsterändens nedre regioner. Se även särskilt i TUNGA
NUKLIDGRUPPENS CERTIFIERING. Grundämnesbildningens relaterade kosmologi
beskrivs här kort från GRUNDÄMNESBILDNINGEN.
GRUNDNUKLIDERNA ¦ 54Xe130 ¦ KURVSKARAN 6C16 ¦ TUNGA NUKLIDGRUPPENS CERTIFIERING ¦ GRUNDÄMNESBILDNINGEN
Max
atomär massdefekt ¦ DEN
KONVENTIONELLA Kärnmassdefekten MISSAR HELA ÄMNESOMRÅDET ¦ MaxMasstal
Modern akademi garanterade sig själv utestängning från
Neutronkvadraten genom 1800-talets nitiska uppfinnarkonster i ämnet Fysik.
Se utförligt i noMACfysik ¦ ATOMVIKTERNA GENOM NEUTRONKVADRATEN ¦ Nuklidkartans gränsvärde ¦
Massdefektsgradientens förklaring ¦
NEUTRONKVADRATENS ÄKTHETSBEVIS
Det faktum att samma
atomära massedefektsvärde (mD) nås på flera olika fusionsgradienter (ellips
eller cirkel) för en och samma atomindivid bevisar, exemplifierar och
garanterar att neutronkvadratens resultatvärden är konsistenta med dess
åberopade geometriska-fysiska morfologi.
Exemplen nedan med fusionsagenterna 3Li6
och 6C16 ger en solid grund för bevisningen med tillhörande kopplingar in i den
tunga nuklidgruppen.
GRUNDNUKLIDERNA ¦ NK basic ¦ 3Li6-GRUPPEN ¦ KURVSKARAN FÖR 6C16 ¦ Udda och Jämna NUKLIDGRUPPERNA
AGENT 6C16
Flera exempel framträder
successivt under arbetets gång med att leta fram sammanhängande exotermiska
fusionsellipser. Exemplen nedan från analysen Maj2020.
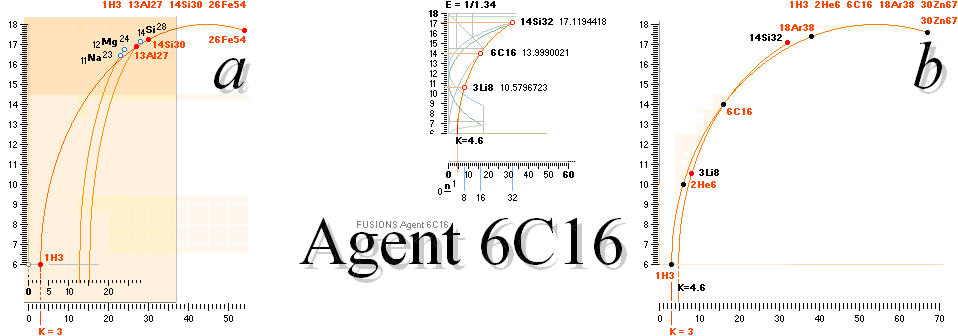
Tabell 1 N144 hExoterm2020test.ods
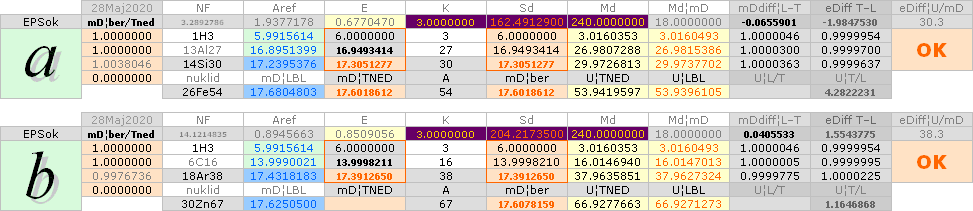
Sammansatthet med
inbördes överensstämmelser utesluter alla tvivel om ATT den geometriskt
utpekade rent fysikaliska morfologin i neutronkvadraten verkligen avtäcker en
genuin naturparadigm: fasta mönsterformer som grundlägger hela atom- och
kärnfysiken. Jämför även i GRUNDÄMNENAS PERIODISKA SYSTEM.
Agent6C16 ¦ 3Li8 ¦ 6C16 ¦ 14Si32
¦
13Al27 ¦ 14Si28 ¦ GRUNDÄMNENAS PERIODISKA SYSTEM
AMax300: NKmax60
NUKLIDKARTANS GRÄNS Amax=300
Bevis:
LBL-tabellens omfattande nuklidkarta i den
tunga nuklidgruppen visar och bevisar att beskrivningen i TNED för
neutronkvadratens nuklidgräns max 300 (eg. 317) är väl förankrad.
LBL-värdena i grafen ovan ser ut att sluta praktiskt taget på masstalet 293
med vissa möjliga vidare spridningar in mot 300.
Med
ovanstående genomgång är hela nuklidspektrets flora av definierade
massdefektsellipser genom Neutronkvadratens formdetaljer belyst och
exemplifierat, enligt här och nuvarande kända förhållanden (Apr2020).
Hur fusionsellipserna beräknas beskrivs
särskilt i FUSIONSELLIPSERNA HUR.
PLANCKRINGEN/Neutronatomens
1818+18+k elektronmassor med
atomära
massdefekternas18-skala i Neutronkvadraten
mD = (1 U/Amn)/me
innefattar
(StabDiff ¦ StabGraf) alla experimentellt kända, observerade och uppmätta
grundämnens atomvikter
U = Amn(1 mDme)
PLANCKRINGEN ¦ NEUTRONATOMENS
INDELNING i elektronmassivet 1818+18+k elektronmassor ¦ NEUTRONKVADRATEN ¦
StabDIFF ¦ StabGRAF ¦ 18-skalan ¦ ELLIPSEKVATIONERNAS
HÄRLEDNING ¦ EXOTERMISKA KÄRNREAKTIONSLAGEN
Genom
neutronkvadratens definition av fusionsellipser
(ELLIPSEKVATIONERNAS
HÄRLEDNING exotermiska fusionsvägar som bildar tyngre exotermiska fusionsprodukter
från lättare fusionsagenter och fusionsobjekt: Grundämnenas successiva
uppbyggnad från lättare till tyngre, se särskilt EXOTERMISKA KÄRNREAKTIONSLAGEN)
omfattas
så varje möjlig exotermisk fusionsprodukt av en specifik ellips vars båge genomskär
minst två, men generellt tre eller flera av de involverade
fusionskomponenternas specifika atomära massdefektsvärden genom
neutronkvadratens fast givna 18-skala.
Atomära massdefektsekvationen
med parametrar fusionsellipsernas definition
mD = 6 + [√(602 [60 (A K)/E]2)]/5
K = Aref(1+ NUKLIDREFERENSMASSDEFEKT/6)
6K = Aref(6+ NUKLIDREFERENSMASSDEFEKT)
E = 1 (Aref)/6
Aref = 6(1E) = 6K/(6+ NF)
= K/(1+
NF/6)
NUKLIDREFERENSMASSDEFEKT = NF
ELLIPSEKVATIONERNAS
HÄRLEDNING ¦
TVÄRELLIPSERNA GEOMETRISK PRINCIPFUNKTION
Fusionsellipsens
exotermiska bevisning för aktuell fusionsprodukt baseras så på
atomkomponenternas garanterat exotermiska
fusionsled i redovisade kvantitetsvärden, typ
5B15 = 2He6 + 1H3 + 2He6
2He6 + 1H3 + 2He6→¦ 5B15:20.99MeV.
= (2He6 + 3Li8 = 5B14) + 0n1
3Li8 + 2He6→¦ 5B14:14.75MeV
¦ + 0n1→¦ 5B15:2.74MeV.
2He6 = 21H3
1H3+1H3 →¦ 2He6:12.20MeV.
3Li8 = 1H3 + 1H2 + 1H3
1H3+1H2+1H3 →¦ 3Li8:21.9MeV
.
MeV = minstEXOTERMISKT AVGIVEN FUSIONSENERGI
MEGAelektronVolt: E=UQ; E/Q=U; (E/e)/T6 = MeV.
ALLA RESULTAT FRÅN EXOTERMISKA KÄRNREAKTIONSLAGENS
KALKYLKORT ;
Atomnamnen matas in typ 2He6, atomvikter tas ut från en
gratis tillgänglig atomviktstabell här LBL-tabellen.
![]()
Basvärdena underkastas sedan beräkningar genom
exotermiska kärnreaktionslagen, resultaten kan direktkopieras.
MeV = minstEXOTERMISKT AVGIVEN
FUSIONSENERGI i MegaElektronVolt: E=UQ;
E/Q=U; (E/e)/T6 = MeV.
fusionsellipsens genomskärning av
fusionskomponenterna agent-objekt-produkt,
gratis tillgängliga atomviktstabeller från
experimentella uppmätningar certifierar resultatens äkthet och möjliggör
jämförande teoretiska resultatbilder.
Både praktiskt exempel och teori visar att
det räcker med att bestämma ett K-värde tillsammans med slutvärden för Sd och
Md ellipsens excentricitet E = Sd/Md med ellipsens genomskärning av
aktuella fusionskomponenter INOM precisionsgränsen 1.0008 eller dess invers
0.9992 med växande noggrannhet mot exakt 1;
De övriga parametrarna NUKLIDREFERENSMASSDEFEKT
och Aref har ingen inverkan på slutresultatet FÖRUTSATT att K-värdet är
bestämt och Sd/Md-värdenas ellipsbåge uppfyller fusionskomponenternas
genomskärning inom precisionsgränserna: det hänger alltså i princip enbart på
att bestämma rätt K-form.
Men vi kan inte alltid
identifiera alla parametrar vilket lämnar den fullständiga fusionsanalysen
ofullbordad.
Vi kan försöka (och gör
det, allt som oftast). Men den analysen blir (ibland) krävande: det finns
(alltid) flera olika sätt (fusionsvägar med olika komponenter) att sammansätta
en given fusionsprodukt. och ellipsbestämningen blir därför (ibland) väl
komplicerad än så länge är det bäst att tillägga: naturvetenskapen utvecklas.
Funktionsexempel, horisontella:
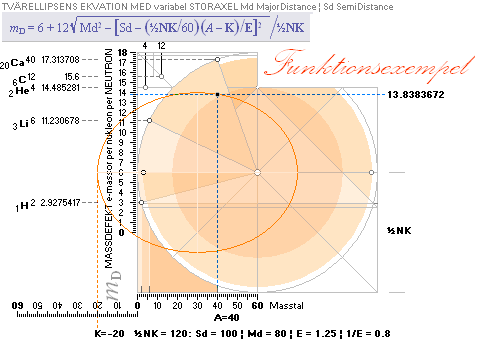
ELLIPSAXLARNAS DEFINITION med Stora Excentricitetstalet E
= Sd/Md görs här med VERTIKAL ELLIPS: Sd=x / Md=y = E.
I fallen med Md=x och Sd=y som ovan ges E-värdet motsvarande
inverterat. Formelkonceptet är detsamma i vilket fall.
NEUTRONKVADRATENS FRAMRÄKNADE
atomära massdefektsvärden mD-villkoren
OM vi kan få fram en ellipsbåge som placerad via ett bestämt K-värde genomskär exotermiskt prövade och verifierade nuklidkomponenters mD-värden
agenten a med objektet o som ska bilda produkten p med i Neutronkvadraten redan kända och bestämda massdefektsvärden (mD) för a och o: vi söker mD(p) från de givna mD(a¦o)
då får mD(p) anses och förstås bestämt OM
![]()
ellipsens bågskärning EPSmD(a¦o) med de redan kända mD(a¦o) uppfyller villkoret
EPSmD(a¦o)/mD(a¦o) = 1.0000000 med sju decimaler, samt att
förhållandet med det så ellipsbestämda EPSmD(p) och motsvarande tabellverks atomviktsvärde (se PRECISIONSGRÄNSEN)
EPSmD(p)/TABELLmD(p) >1.0008 eller > 1/1.0008, eller allra helst bättre typ
EPSmD(p)/TABELLmD(p) >1.00002 eller > 1/1.00002
för att säkra och garantera överensstämmelsen mellan experiment och teori;
De största avvikelserna man finner i jämförelse mellan mellan olika tabellverks atomviktsvärden (för huvuddelen av de stabila nukliderna) ligger i storleksordningen just 1.00002 och mindre. Med vidare hänsyn till laddning-massa-förhållandet
(Z/A)(me/mn) <= max 1.0002 enligt gängse tabellverk som blotta grundvalen för de instrumentella atomviktsmätningarna över huvud taget, utgör dessa värden område för en teoretisk precision som vi måste beakta i prövningen av varje atomteori och dess anspråk på jämförande atomviktsvärden. Exakt hur dessa antydda precisionsgränser ska tolkas vet vi inte riktigt: etablerad kärnteori har ingen TNED-parallell, ingen jämförande Modern Neutronkvadrat. Så, vi eftersträvar (enbart) »största möjliga precision» med ovan givna preferenser.
BelysandePrecisionsExempel: mD-villkoren
BELYSANDE PRECISIONSEXEMPEL
NEUTRONKVADRATEN ¦ STABdiff ¦ Jämförande diagram CODATA/HOP ¦ WeizsäckerEkvationen ¦ TNED ¦ Precisionsexempel Järntoppen
Vertikalskalan numeriskt med förhållandet mellan experimentellt uppmätt och teoretiskt beräknat:
Neutronkvadratens
beräknade atomära massdefekter omräknade till atomvikter och jämförda med
gängse gratis tillgängliga atomviktstabeller [HOP, CODATA, LBL, alla dessa är
jämbördiga med smärre differenser gott och väl inom området 1.00005 för
huvuddelen av nukliderna med masstalen 0-123, se Jämförande HOP/CODATA] ligger alla inom området ±1.0001. Den moderna akademins
motsvarande teoretiskt framräknade värden (Weizsäcker) ligger så långt utanför
dessa marginaler att de är helt ointressanta i jämförelserna, särskilt de
första sex stabila nukliderna, se StabDIFF. Den mest avvikande läppen ovan
som sticker ut mest här är Järntoppens toppmassdefektsnuklid (26Fe56). Den
beräknades (originalen här från 2003) efter UddaJämna fusionsellipserna med
deras (approximerade) vågfunktion och utan den mera preciserade kännedom om det
aktuella gränstoppvärdet närmast under toppgränsen 18. Vi ska strax återkomma
till de senare kunskaperna (Maj2020) om precisionen i den känsliga punkten.
Nämligen
experimentalfysikens olika metoder med uppmätningen av atomvikterna. Den
mätningen baseras genomgående på ett laddnings-massaförhållande (WIKIPEDIA: Atomic
mass ¦ Mass spectrometry [Maj2020] .. is
an analytical technique that measures the mass-to-charge ratio of ions).
Vi kan undersöka en teoretisk maxgräns i ONOGGRANN PRECISION (OP) för varje
tabellerad nuklid med uppgift om atomnumret (Z), masstalet (A) och massorna för
elektron (me) och neutron (mn) genom sambandet OPmax
= (Z/A)·(me/mn).
Vi finner att
huvuddelen (LBL-tabellens 3180 nuklider) med smärre avvikelser ligger i området
1.0005nnn och neråt
mot 1 (LBL-tabellens
minsta värde visar ett 0.0000777).
Nu är den maxgränsen (vad vi vet) INTE
direkt aktuell i massspektrografernas atomviktsmätningar men till viss här
inte närmare känd del. Atomkärnorna måste nämligen tvunget först joniseras,
elektronexciteras, för att sedan kunna accelereras fram till den avlänkande
(traditionellt apparatspektrografiska) magnetiska avböjningsanordningen. Vilket
innebär att mätningen av atomvikter INTE görs på Neutrokkvadratens idealt
geometriska (som den får förstås) stillastående nuklidobjekt aktuellt
idealt vilandeATOM. Kortare: Atomens kärna måste dels exponeras och dels
befinns sig i markant rörelse = ha tilldelats särskild rörelseenergi för att
mätningen alls ska kunna genomföras. Resten är statistik och utvärderingar med
mest noggranna resultatbild baserat på någon viss minsta MÄNGD av den
aktuella atomgruppens individer. Dessutom har vi att ta hänsyn till de olika
epokernas något marginellt olika standardvärden (elektron och
neutronmassorna, atomära massenheten, Plancks konstant).
Sammantaget blir det omöjligt att komma
ifrån en viss (här inte närmare känd) osäkerhet i jämförelsen mellan
experimentella tabelldata och Neutronkvadratens EGNA atomnuklidvärden.
EXEMPEL.
Neutronkvadratens mest exakta egna nuklidreferens är Heliumnivåns egna atomära
massdefektsvärde
mD(2He4) = 14.485281374 = 6 +12/√2. Med HOP-källans värden för elektronmassan, neutronmassan, och
det här använda värdet för atomära massenheten 1.66033 t27 KG (ENCARTA99) blir atomvikten
U(2He4) = Amn(1
mnme) =
4.0025990u = Neutronkvadratens absolut garanterat
statiska ideala atomviktsvärde.
HOP-tabellens
atomviktsvärde för Heliumatomen 2He4 anges
4.00260312u med HOP-värdet u= 1.66043 t27
KG.
LBL-tabellen ger
motsvarande 2He4 atomviktsvärde
4.0026033u = LBL-tabellens värde (här inte närmare
känt u-värde).
Jämförande största
förhållandet mellan atomviktsvärdena blir
HOP/NK = 4.00260312/4.0025990 = 1.000 0010 35
LBL/NK = 4.00260330/4.0025990 = 1.000 0010 80
Det är alldeles uppenbart
att vi i det exemplets ljus befinner oss bortom varje begripligt ifrågasättande
kritik angående PASSNINGEN mellan Neutronkvadratens idealt statiska geometriskt
utpekade atomviktsvärde och det rent experimentellt uppmätta. Vi kan här
veterligt inte påvisa någon som helst avgörande principiell skillnad;
differenserna ligger tydligen inom storleksordningen en miljondel. Och då
känner vi (här) fortfarande inte till hur de nödvändiga rörelseenergierna
påverkar den kvoten för att alls få till stånd en masspekroskopisk
atomviktsmätning.
Neutronkvaratens
grundnuklider 1H1 1H2 1H3 2He3 2He4 (GN) i samma typ av jämförelse befinner sig i stort i samma
område: det skiljer på ental miljondelar. Generellt för Neutronkvadratens
samtliga värden de ursprungligen (från 2003) beräknade värdena som i
StabDIFF-jämförelsen ovan ligger de största avvikelserna i området ± 1.0001.
Precisionsgränsen för de teoretiskt beräknade värdenas meningsfullhet är
±1.0008. Större värden gör hela teorin praktiskt taget helt och hållet
värdelös.
Det vore också
sensationellt om neutronkvadratens värden vore exakt identiska med de
experimentellt uppmätta. Vi bör under alla omständigheter alltid finna vissa
differenser »inte för stora» mellan statik och dynamik.
Sambansformerna
samlade
TVÄRELLIPSEN MED FAST
STORAXEL:
mD = 6 + [√(602 [60 (A K)/E]2)]/5 ;
TVÄRELLIPSEN MED VARIABEL
STORAXEL:
mD = 6 + 12[√(Md2 [Sd (240/60)(A K)/E]2)]/240 ;
mD = 6 + 12[√(Md2 [Sd (½NK/60)(A K)/E]2)]/½NK ;
Gemensamma Enheter för
Sd Md NK (pixels illustrativt).
mD = 6 + 12[√([Md/½NK]2 [Sd/½NK (1/60)(A K)/E]2)]
6C16
+ 20Ca40 = 26Fe56 → 39.11 MeV
................... stabil: Järn
Vi har tidigare
beräknat Neutronkvadratens fasta och helt statiskt ideala mD-värden för
atomnukliderna 6C16 och 20Ca40. Vi har också kontrollerat exotermiska
fusionsvägar för dessa enligt fusionsleden
6C16
+ 20Ca40 = 26Fe56 →
39.11 MeV stabil Järn
6C16 + 20Ca40 + 6C16 = 32Ge72 → 64.57 MeV stabil
Germanium
6C16 + 26Fe56 = 32Ge72 → 25.45 MeV stabil Germanium
6C16 + 26Fe56 + 6C16 = 38Sr88 → 54.23 MeV stabil
Strontium
MeV, minsta avgivna exotermiska fusionsenergin enligt
exotermiska kärnreaktionslagen
Ovanstående
fusionsled antyder kräver, säger Neutronkvadraten att vi också bör ska
kunna bestämma mD-värdet för Järnindividen 26Fe56 ur mD-talen för
agenten 6C16 och objektet 20Ca40 enligt (mD-villkoren) allmänna atomära
massdefektsekvationen
Resultat
efter genomförd (manuell) prövning:
IronTop: Maj2020 JÄRNKÄRNAN
ELLIPS-Skaran
6C16 ¦ Formationen
av fusionsagenten 6C16 ¦ ExoEx
a: Vi matar
in fusionsagent 6C16 och fusionsobjekt 20Ca40 i exotermiska kärnreaktionslagen
för att certifiera fusionsproduktens exotermiska natur; Det gjort använder vi
sedan fusionsellipsernas iterationsalgoritm för att hitta den
fusionsellips som innefattar agent, objekt och produkt: agent och objekt matas
in och eftersom atomära massdefektens elliptiska funktioner, verkligen,
definierar exotermiska fusioner, omfattas/tangeras/vidrörs produkten
automatiskt av den framitererade ellipsbågens skärning, eller ska i vart fall
göra det, »enligt Neutronkvadratens anvisningar».
Det
iterationsresultatet är, emellertid, bara en råform: ännu så länge (tills
vidare) måste en slutlig manuell precisionsiteration genomföras för att få fram
den ellipsbåge som ger definitionsgaranti (L/T=T/L=1.0000000) på den
identifierade produktkandidaten 26Fe56: Ellipsbågen måste skära/tangera tre
nuklidpunkter i nuklidkartan över horisontella ellipsaxeln. Resultatet
garanterar/bevisar samhörigheten.
KALKYLKORTET ¦ Fusionsellipsernas iterationer ¦ Fusionsellipserna
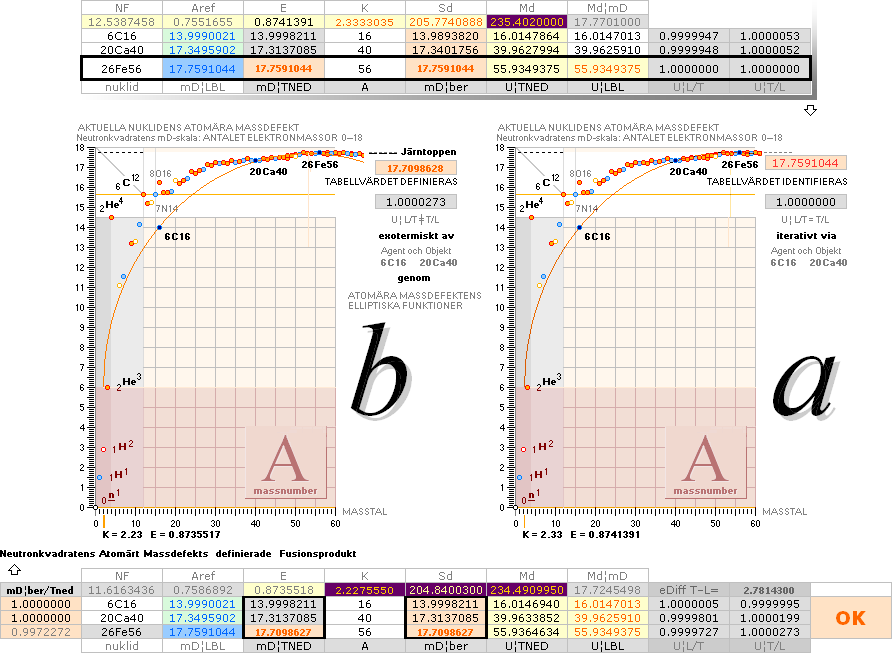
Tabell 1 O15 hExoterm2020test.ods
ITERATIONSellipsens egna mD-värde för 26Fe56 från egna
NK-bestämda 6C16¦13.9998211
och 20Ca40¦17.3137085 : 26Fe56¦17.7098627
U från mD: U = Amn(1 mDme); mn neutronmassan 1.0086652u, me
elektronmassan 0,000548598u, u 1.66033 t27 KG, se HOP-referenserna.
b: Den
egentliga neutronkvadratens definition av fusionsproduktens 26Fe56 atomära
massdefektsvärde mD från agentens och objektets mD-värden enbart
genom neutronkvadratens försorg: fusionsproduktens experimentellt
oberoende mD-värde. Så, kan vi utvidga TNED-värdena för vidare
jämförelser.
Om allt stämmer, ska
differensen mellan det värdet omräknat i atomvikt och tabellvärdets atomvikt
för fusionsprodukten ligga i storleksordningen ental elektronmassor (vad vi
kan sluta oss till handlar om differenserna mellan nukleära och atomära
bindingsenergier tillsammans med de nödvändiga joniserande ingreppen för att
alls kunna få fram mätdata på atomvikter men vi har här inga som helst säkra
basdata på hur det förhåller sig med dessa differenser: modern kärnteori har
inte Neutronkvadraten: jämförelser saknas)
(Se WIKIPEDIA: Atomic
mass ¦ Mass spectrometry [Maj2020] .. is
an analytical technique that measures the mass-to-charge ratio of ions).
Vi utnyttjar så ellipsplaceringen i a
som bas och fortfarande manuellt krävande
men ytterst givande och stimulerande tills vi ev. kan utforma en mera avancerad
itererande maskinordning
itererar fram slutvillkoret:
Ellipsbågens ekvationsresultat (variabler K Sd
Md: Sd/Md=E)
måste, tvunget, innefatta de redan givna mD-värdena för fusionsagenten 6C16 och
fusionsobjektet 20Ca40 exakt in till sista (här 7:e) decimalen: jämförelserna
måste, tvunget, sluta på 1.0000000.
När det inträffar, är fusionsproduktens
motsvarande experimentellt mätoberoende mD-värde definierat.
eDIFF
(Neutronkvadraten¦TNED-beräknat minus Experimentellt uppmätt) i kalkylremsan
visar atomviktsdifferensen i antal elektronmassor för ev. vidare utvärdering. RESULTATBILD:
Neutronkvadratens identifierade
atomära massdefektsvärde mD för
den exotermiska
fusionsprodukten 26Fe56 enligt fusionsledet
6C16
+ 20Ca40 = 26Fe56 →
39.11 MeV stabil Järn
mD(26Fe56) = 17.7098628 med motsvarande atomvikt U=Amn(1mDme)
¦ mnme
U¦TNED =
55.9364634; Experimentellt uppmätta (LBL-tabellen):
U¦LBL =
55.9349375; förhållande största:
U(TNED/LBL) = 1.0000273
............... certifierad
under övre gränsen 1.0008.
Differens i e-massor =
2.7814210
StabDIFF ¦
Jämförelserna i StabDIFF
med ovanstående 26Fe56-resultat violetta punkten, vänster ersatt av föregående
(originalet 2003 höger). Tidigare mera allmänna värden från
UddaJämna-ellipsernas vågfunktioner visar hur precisionen i jämförelsen med
experimentellt uppmätta atomvikter avsevärt förbättras. Så har vi också att
förvänta för resten av toppnukliderna (Järnisotoper 57¦58, Nickel 58, Kobolt
59) runt masstalen 56-60. Dessa värden är här i skrivande stund ännu inte
framräknade. Se vidare pågående utvecklingar i U¦eDIFGFen.
EPS16-skaran: IronTop
NEUTRONKVADRATENS EXEMPEL
Precisionen i
ellipstangenternas atomära massdefektsvärden bevisar tillförlitligheten i
TNED-matematiken: Neutronkvadratens elliptiska funktioner
FUSIONSAGENTEN 6C16 MED EXOTERMISK FÖRDJUPNING IN TILL
TUNGA NUKLIDGRUPPEN
Lätta nuklidgruppen:
masstalen 1-60 ¦ Tunga nuklidgruppen: resterande 60+ till nuklidkartans slut.
PRIMÄRA ELLIPSITERATIONER
PRECISIONSEXEMPEL ¦ 6C16-grunderna ¦ Masstalsgränsen 300
På alldeles samma sätt
som PRECISIONSEXEMPEL i föregående fall kan vi bestämma den experimentellt
oberoende neutronkvadratens atomviktsvärde för i princip samtliga nuklider
också i den tunga nuklidgruppen: Nukliderna med masstalen 60+ fram till änden
(max 300). Figuren ovan med kurvskarans 7 individer exemplifierar hur
fusionsagenten 6C16 rent exotermiskt förmår bilda tyngre nuklider fram till
gränsnukliden 56Ba136. För att komma än vidare i den tunga nuklidgruppen, måste
en annan agent anställas med lägre massdefekt. Vi måste dock, som i föregående
fall, iterera fram varje enskilt mD-värde explicit för varje specifik
fusionsprodukt som i b-fallets precisionsexempelbeskrivning; Vad vi vet
(än) finns ingen enkel genväg vid sidan av den manuella iterationsproceduren
för att snabba upp tiden fram till ett resultatvärde (i början tar det timmar
att iterera fram ett slutresultat manuellt).
Vi anställer fusionsellipsen
som ska sluta på produkten 32Ge72 och
finner efter visst arbete:
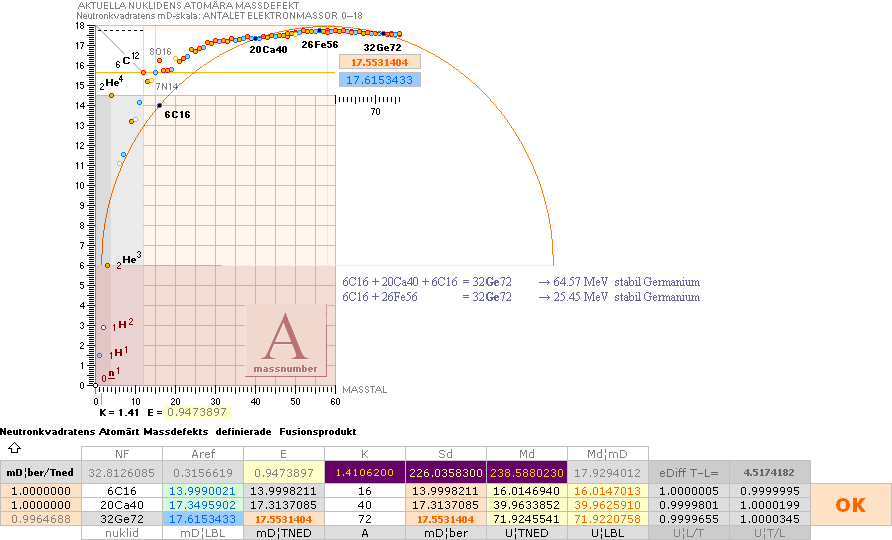
Tabell 1 O27 hExoterm2020test.ods
NK-mD-bestämda 6C16 och 20Ca40 NK- beräknar mD för 32Ge72¦17.5531404
Neutronkvadratens
identifierade atomära massdefektsvärde mD för
den exotermiska
fusionsprodukten 32Ge72 enligt fusionsleden
6C16
+ 20Ca40 + 6C16 = 32Ge72
→ 64.57 MeV stabil Germanium
6C16
+ 26Fe56 = 32Ge72
→ 25.45 MeV stabil Germanium
mD(32Ge72) = 17.5531404 med motsvarande atomvikt U=Amn(1mDme)
¦ mnme
U¦TNED =
71.9245541; Experimentellt uppmätta (LBL-tabellen):
U¦LBL =
71.9220758; förhållande största:
U(TNED/LBL) = 1.0000345 ............... certifierad under övre gränsen
1.0008.
Differens i e-massor =
4.5174182
Vi anställer på samma
sätt en fusionsellips som ska sluta på
produkten 38Sr88. Vi får:
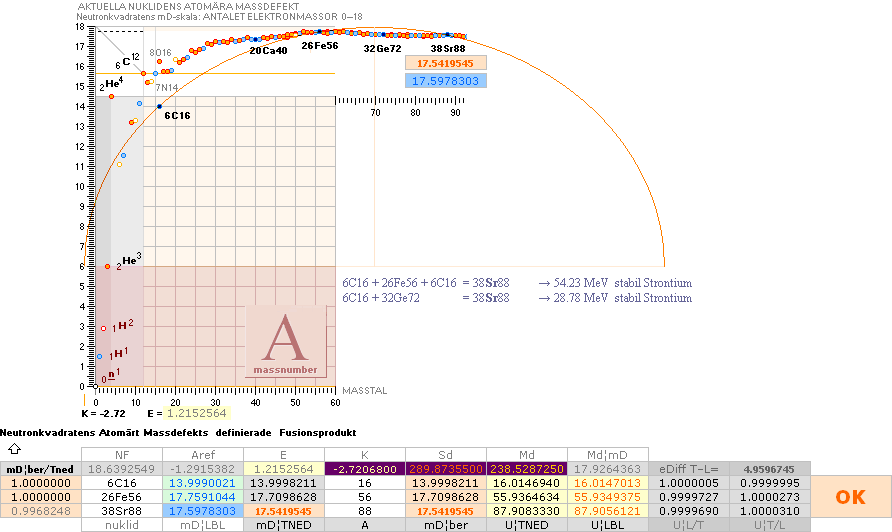
Tabell 1 O38 hExoterm2020test.ods
NK-mD-bestämda 6C16 och 26Fe56 NK- beräknar mD för 38Sr88¦17.5419545
Neutronkvadratens
identifierade atomära massdefektsvärde mD för
den exotermiska fusionsprodukten
38Sr88 enligt fusionsleden
6C16
+ 26Fe56 + 6C16 = 38Ge88
→ 54.23 MeV stabil Strontium
6C16
+ 32Ge72 = 38Ge88
→ 28.78 MeV stabil Strontium
mD(38Sr88) = 17.5419545 med motsvarande atomvikt U=Amn(1mDme)
¦ mnme
U¦TNED =
87.9083330; Experimentellt uppmätta (LBL-tabellen):
U¦LBL =
87.9056121; förhållande största:
U(TNED/LBL) = 1.0000310
............... certifierad
under övre gränsen 1.0008.
Differens i e-massor =
4.9596745
METODIKEN för att härleda
Neutronkvadratens egna rena mD-värden består alltså i att som en
MARKVÄXT bygga nerifrån (fröet) på primärt fasta givna mD-individer,
utnyttja deras värden med vidare föreningar/fusioner »uppåt Solen», och så få
fram resultatvärden för allt tyngre nuklider.
eDIFFen: U¦eDIFFen
eDIFF-värdet?
Den intressanta frågan
här är eDIFF-värdet. Ett uppslag:
Atomvikter kan
omöjligen mätas på atomer utan att utsätta dem för en eller annan påverkan.
Så: hur får vi veta
vilka differenser i real massa som gäller om alls i förhållandet mellan
normalt vilande atomer neutronkvadratens fall och dem som figurerar i en
massspektrograf: Har eDIFF-värdet här någon koppling?
Med en enklare
utvärdering med hjälp av redan experimentellt kända sambandsformer är svaret på
den frågan ett entydigt:
Nej. eDIFF-värdets
storleksordning (differens i flera elektronmassor) är alldeles för stor för att
koppla massökningseffekter eller andra liknande detaljer inom masspektroskopin.
Differenser finns där, naturligtvis. Men i de flesta fall bara obetydliga
bråkdelar av elektronmassan (typ 0.002) och med de accelerationsspänningar (max
25 KV) som massspektrograferna använder (enligt viss litteratur):
Med
accelerationsspänningen 25KV för objektsatomen via en dess förberedande
jonisation (atomen joniseras genom att beröva den en elektronbindning)
på en elektron (Q=1e=1.602 t19 C), får vi exempelvärden i tilläggsmassa:
A = 1 ........... eDIFF= 0.049;
A = 100 ....... eDIFF = 0.00049, A masstal.
Inte heller differenser inom de olika
epokernas standardvärden neutronmassa, elektronmassa, atomära massenheten,
eller de olika tabellverkens något olika atomviktsvärden har någon inverkan.
Dessa skillnader är i dessa sammahang helt försumbara.
Jämförande Grundnuklider: eDIFFen
Föregående
fusionsellipser i exempel
Exempel Järntoppen
6C16+20Ca20=26Fe56; .............. mDdiff
= 0.05e ¦ Udiff = 2.87e ¦ faktor: 2.87/0.05 = 57.4;
Exempel Germanium
2(6C16)+20Ca20=32Ge72; ........ mDdiff
= 0.06e ¦ Udiff = 4.52e ¦ faktor: 4.52/0.06 = 75.3;
Exempel Strontium 2(6C16)+26Fe56=38Sr88; ......... mDdiff = 0.06e ¦ Udiff = 4.96e ¦
faktor: 4.96/0.06 = 82.7;
mD-differenserna i atomviktsenheternas slutform ger alltid
värdet Amn: Omräkningen
Faktor/A=neutronmassan.
Vi noterar att GRUNDNUKLIDERNA inte alls ansluter
till större avvikelser snarare till nyssnämnda område för mätapparaturen,
eDIFFen;
SAMBANDSFORMERNA med slutvärdena högra har formen (U¦L U¦T)/(mD¦L mD¦T) = masstalet A som ger slutvärdet
A·mn:
Divideras slutvärdena höger med resp. masstal A ges i
samtliga fall konstanten neutronmassan i u-enheter 1.0086652.
Tabell 1 C52 hExoterm2020.ods
Neutronkvadratens grundnuklider avviker
obetydligt i atomvikterna från de experimentellt uppmätta värdena. Till och med
så litet att avvikelserna tangerar den spektroskopiska apparaturens smärre avvikande
kvantiteter i massa för att alls få till stånd en mätning exemplet ovan med
25KV accelerationsspänning för en en-elektron-joniserad atomkärna med masstalet
A=1: max 0.049e. Exakta praktiska apparatvärden är här inte närmare kända:
Olika laboratorier har egna specifikationer [som inte lämnas ut gratis till
allmänheten, vad vi vet]. Precis information är svår att få fram.
Särskilt för 2He4-individen [1e-joniserad]
ges massavvikelsen 0.0077e med en accelerationsspänning på 15.8 KV. Det var ju
upplysande.
NEUTRONKVADRATENS FUSIONSELLIPTISKA MORFOLOGI (formlära)
EN DEL (grundpremisser,
för ev. vidare) KAN VI KLARLÄGGA GENOM RELATIVT ENKLA BEVIS:
Beviset för unik
fusionsellips
ILLUSTRATIONEN TILL ba-komplexet:
GIVEN FIXERAD FAST
HORISONTELL PLACERING för Ellipsaxeln:
För en fast given xy-punkt
(A;mD) över horisontella ellipsaxeln finns obegränsat många ellipser
som skär xy-punkten: Konsekvens/Bevis:
För en annan fast
given xy-punkt (A;mD) över horisontella ellipsaxeln
finns således inget annat än bara
en enda unikt given
ellips som skär bägge de fast och fixt
givna xy-punkterna:
Given horisontell
ellipsaxel:
Två olika ellipser existerar inte som bägge
skär två eller flera fixt givna xy-punkter över horisontella
axeln;
Två eller flera fixt givna xy-punkter
över horisontella axeln kan bara skäras av en enda unik ellipsbåge.
Given fusionsagent (A;mD)1
och fusionsobjekt (A;mD)2 definieras av en unik fusionsellips;
Andra (A;mD)-värden kopplar
andra fusionsellipser och därmed andra fusionsprodukter (A;mD)3.
Given fusionsagent (A;mD)1
och fusionsobjekt (A;mD)2 definierar en unik fusionsprodukt (A;mD)3;
Nämligen det första att
klargöra (eDIFFen):
EXPERIMENTELLT UPPMÄTTA ATOMVIKTER KOPPLAR INTE
FUSIONSELLIPSERNA EXAKT
trots en relativt hög
precision i den allmänna utvärderingen (men det finns exempel som ligger
väldigt nära):
FUSIONSPRODUKTEN MISSAS
MED RELATIVT STORA BELOPP vilket bevisar påståendet
Vi studerar ba-exemplet
med Järntoppen
Tabell 1 Q23 hExoterm2020.ods kortet används genomgående för olika värden
med olika noggrannhet beroende på analys
Tabell 1 O32 hExoterm2020test.ods
a-delen är (FIRST) bara en approximativ ellips som används
(vi utnyttjar tabelldatat som grund) för mera preciserad manuell
iteration.
b-delen är neutronkvadratens exakt motsvarande
framitererade exotermiska fusionsellips i fusionsledet
6C16+20Ca40=26Fe56
värdena visas i b-originalet (bildlänken ovan).
TESTAR VI DIREKT på de
experimentellt uppmätta atomvikterna (Uu) genom mD-omräkningen
mD=(1U/Amn)/me och på den
vägen (SECOND) söker fusionsprodukten (26Fe56) från de experimentellt
motsvarande mD-komponenterna (13.9990021 och 17.3495902) hamnar vi på
tok långt över det experimentellt uppmätta värdet 17.7591044. Nämligen
(blå ellipsbågen i a) på nivån 17.8555083.
Avvikelsen i atomvikt
eDIFF=5.45e är dessutom galet stor (antyder inverkan av ett möjligt
systemfel). Slutsats:
Direkt EXPERIMENTELLT UPPMÄTTA ATOMVIKTER
DIREKTKOPPLAR INTE direkt uppmätta atomviktsvärden för NEUTRONKVADRATENS
(NK) FUSIONSELLIPSER;
Tabellvärden
för atomvikter i Neutronkvadraten U¦agent+objekt kopplar inte U¦produkt
exakt. Ifall nu någon hade trott det.
Varför inte då?
DÄRFÖR ATT
NK-matematiska fysiken INTE inbegriper masspektroskopins massmätande
jonisationskomplex som innebär en icke möjlig närmare exakt specificerbar
störning i det naturliga atomkomplexet.
NK-matematiska fysiken mäter på helt
naturliga atomer som blir omöjligt att kontrollera så snart en fysisk
mätprob införs i ett naturligt atomgitter.
En ATOMS MASSA som specifik för en atoms
masstal (och atomnummer) är vad vi har förstått helt och hållet
temperaturoberoende. Det skulle motsvara Neutronkvadratens rent
geometriskt-fysiska fundament: garanterat noll joniserande inverkan för »exakt
naturmassa» (som vi alltså inte närmare kan kontrollera ..).
Masspektroskopin däremot bygger på en
tvungen excitation (elektronkapning = atomär massreduktion) av ett STORT
antal atomer i samma familj, och därmed ett utspritt medelvärde i slutänden som
också avhänger jonisationens (eventuella) inverkan relativt icke-joniserade
tillståndets fysik.
Ifall nu någon hade trott
något åt »det exakta hållet». Neutronkvadratens inneboende matematiska
morfologi kopplar inget atom mass mätande jonisationskomplex.
Vilket skulle bevisas (med Järntoppen som
skolexempel).
Gernom att jämföra experimentellt uppmätt
med NK-värdena får vi i vilket fall en noggrann bekräftelse på vad som är vad i
sammanhanget: se DIFFgraferna.
Det är tydligt att Experimentellt + TNED = Sant.
DET SAGT 8O18 ett starkt närliggande exempel:
a: Komponenterna
1H2 och 8O18 insätts i iterationsalgoritmen för en neutronkvadratens
fusionsellips (iterationsEllipsens storaxel här alltid lika med vertikala
neutronkvadratens sida [240pixels]). Värdena som kommer fram K och E på givna
A=2 och 18 insätts i (b) allmänna massdefektsekvationen;
8O18 TNEDbasics
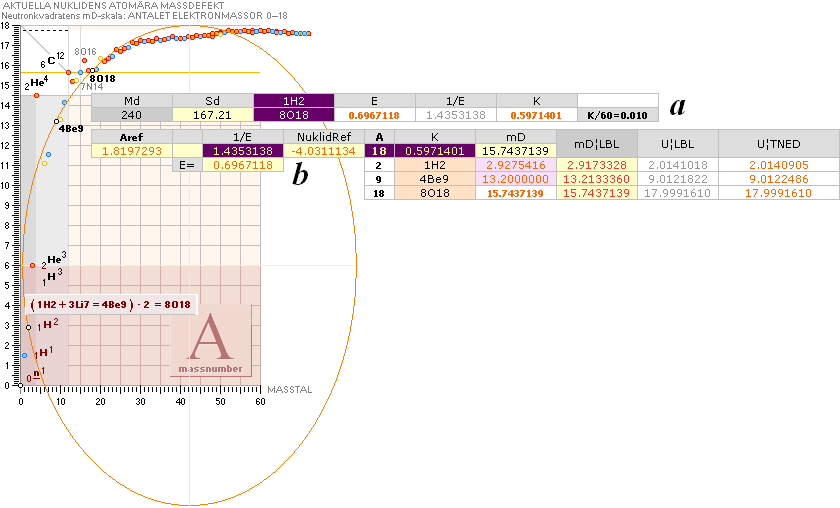
Tabell 1 B163 hExoterm2020.ods,
Tabell 1 Q53 hExoterm2020test.ods
b: Allmänna
Massdefektsekvationen mD = 6 + SIGN(A 6)√(602 [60
(AK)/E]2) räknar ut mD-värdena för respektive masstal A={2,9,18}.
Aref och Nuklidreferensvärdena beräknas automatiskt med givna KE,
Aref = 6(1E),
NuklidRef = 6(K/Aref 1).
SIGN(A 6) behövs för att få korrekt värde med mD-tal mindre
än 6: SIGN=1 för dessa fall.
Och som vi ser,
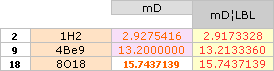
ligger de så beräknade mD-värdena
nära de motsvarande experimentellt uppmätta (LBL-tabellen) exakt för
8O18-nukliden.
UPPSLAGET med den
(relativt) enkla ellipsiterationens resultat i a leder oss så till en
ren Neutronkvadratsbestämning av atomära massdefekten för just nuklidindividen
8O18 (nära, men inte exakt samma ellips):
ATOMÄRA MASSDEFEKTSVÄRDET FÖR 8O18
enligt Neutronkvadratens anvisningar: 15.7262112 elektronmassor ¦ 4Be9 ¦ 1H1

NK-mD-bestämda 1H2 och 4Be9 NK- beräknar
mD för 8O18¦15.7262112
eDiff¦U/mD-värdet används här endast som
ett kontrollvärde: slutar alltid på samma konstant; aktuellt masstal A ×
Neutronmassan 1.0086652u: eDIFF-värdet dividerat med A ger alltid 1.0086652.
Iterationsarbetet för att få fram ovanstående OK är
fortfarande krävande (upp mot eller mer än timmen) då ännu en utformad
iterationsalgoritm saknas för ellipser med tre bågkomponenter (Vidare utvecklat längre fram).
Slutresultat: Neutronkvadratens mD(8O18) = 15.7262112. LBL-tabellen ger
15.7437139.
Vi noterar att de
automatiskt givna värdena för Aref och NF (nuklidreferensen) i fallet
8O18 INTE har (här, ännu) någon motsvarande genomlyst fusionsanalys (enda
ledtråd: 1.8 = 9/[5=72]; 3Li7 ligger vid sidan av ellipsen). Vi nöjer oss med
att bevisa det motsvarande exotermiska fusionsledet enligt resultaten från
exotermiska kärnreaktionslagens kalkylkort:
1H2 + 3Li7 = 4Be9 →
16.55 MeV ¦ + 4Be9 = 8O18 → 23.27 MeV
I neutronkvadraten går vi (alltså) istället »åt andra hållet»:
HELT SÄKERT MED EXPERIMENTELLT UPPMÄTTA ATOMVIKTER
ICKE EXAKT ÖVERENSSTÄMMANDE VÄRDEN
U¦agent+objekt = U¦produktKOPPLAR SAMTLIGA
EXOTERMISKT
BEVISBARA FUSIONSKOMPONENTER
som genomskärs av en och samma fusionsellips allmänna
atomära massdefektsekvationen
är den enda bevisform vi känner för att kunna härleda
atomvikter med närmast möjliga exakta
precision mot experimentellt uppmätta värden genom
Neutronkvadraten
MED SÅ TILLRÄCKLIGT STOR NOGGRANNHET
att vi kan postulera överensstämmelser i synnerhet för
grundnukliderna som uppvisar så små differenser att dessa tangerar områdena för
mätapparurens noggrannhet eller onoggrannhet.
Men vi behöver laboratoriernas mera noggranna
apparatspecifikationer för masspektroskopisk mätning för att kunna avgöra den
frågan mera ingående.
BETRÄFFANDE
GRUNDNUKLIDERNA i sammanhanget:
Grundnukliderna har
ingen gemensam eller över huvud taget någon fusionsellips alls att referera
till i Neutronkvadraten (NK). Enbart NK som sådan. Grundnuklidernas mD-värden
utgår ifrån andra tydligen geo-matematiskt morfologiska premisser: En fast
(NK) fixerad GEOMETRISK bas. Därför kan vi heller inte anställa någon direkt
fusionsbaserad experimentell jämförelse. Vi har endast de jämförande
atomviktsvärdena att ta hänsyn till i prövningen: Neutronkvadratens värden
kontra de experimentellt uppmätta.
GRUNDNUKLIDERNA ¦ Jämförande Grundnuklider
TRIPELBESTÄMNINGAR unika mD-värden i
Neutronkvadraten
2020V23
27Co59 = 2He4 + 7N15 = 9F19 ¦ + 18Ar40 = 27Co59
¦ = 6C14 + 21Sc45 ¦ NKmD(27Co59) = 17.6695552 ¦ LBLmD:
17.7057143;
DESSA FÖREFALLER YTTERST
SVÅRA ATT FINNA KOPPLINGAR TILL flera försök, alla misslyckas .. :
20Ca48 är felräknad i
Exoterm 2020test.ods ? ...
20Ca48 = 5B11 .. + 10Ne20 .. [+ 8O19] ellipsen (underligt ..)
stämmer (någorlunda ..) på 23Vanadin50
( 2·5B11 = 10Ne22, +
10Ne20 = 20Ca42, + (3Li8=2He6+1H2) = 23V50 ..)
20Ca48 → 4(1H3) +
2(8O18) → EPSok (tydlig fusionsring 1H3 3Li7 8O18 ..
inga diskreta par ..) MEN MISSAR MÄRKBART PRODUKTEN 20Ca48, snarare 22Ti48
mD17.62. Mysko ..
Exoterm2020test.ods¦P147:
Ett annat sätt för
20Ca48:
2(2He6 + 8O18 = 10Ne24) = 20Ca48 → EPSok;
Men iterationen vill peka
divergent: hopplöst fall. Råformens tripelellipspunkter stämmer bäst, men dessa
är tabellvärden;
mD-beräkningen ger
17.3839377 mot LBL-värdet 17.4465374. Det skiljer på 3.032 e-massor i
U-värdena.
SOM DET VERKAR: Det krävs
mellanliggande instabila nuklider i blandningen för att få fram tyngre. Inte
alltid, men tydligen särskilt.
LÖSNING 20Ca48 Exoterm2020test.ods¦N170: 17.4795692; eDIFF=
1.5992677.
26Fe58 = 6C16 + 20Ca42 ingen lätt match .. hittar ingen
3-koppling ..
(2He4 + [2(2He3) =
4Be6] = 6C10) + 20Ca48 = 26Fe58 →
17.8109723 ¦ LBLmD: 17.7384857; U¦eDiff¦TL = 4.2406556 (möjligt fel);20Ca48
5B11 ¦ 10Ne10 ¦ 20Ca48 ... troligen fel ..
2He4 ¦ 20Ca48 ¦ 26Fe58 → 2He4 +
(2·2He3=4B6) = 6C10 ¦ + 20Ca48
ALLA STABILA nuklider:
Tabell 1 O46 hExoterm2020test.ods

Tabell 1 O73 hExoterm2020test.ods

Iterationerna visar och
bevisar att vertikala ½NK-längden ingalunda utgör någon absolut maxgräns för en
fusionsellips. Den kan tydligen lika väl som vara mindre också vara större än
grundnuklidernas tvärellipstiska grundaxel, ½NK.
Tabell 1 O94 hExoterm2020test.ods

Enkelellipsen som avslöjade lösningen ovan:
Frånsett 44Ru104-nukliden
den skiljer på två pixels = 1/10 elektronmassa: Avvikelserna mellan
Neutronkvadratens beräknade mD-värden och de från tabellerna är
omärkligt åtskilda. Ingen skillnad framgår i figurens skala.
Tabell 1 O80 hExoterm2020test.ods

Tabell 1 O87 hExoterm2020test.ods

2020V16
TRIPELITERATIONERNA
NEUTRONKVADRATENS SIDA:
NK=240pixels:
Trepunkts
Iterationsellipser via Sd Md och K på givna mD-värden från fusionsagent och
fusionsobjekt med given fusionsprodukt ZnamnA vars mD-värde söks:
Tre eller flera givna
punkter på en given ellipsbåge kan
omöjligen också omfattas av någon annan ellipsbåge än den givna. Nämligen
punktparens inbördes TANGENTER: lutningsvinklarna mellan parpunkterna är unika
för varje unikt given ellips (Sd/Md=E) och kan omöjligen ändras om de
nödvändigtvis ska vara unika.
TVÅ PUNKTER DÄREMOT en
enda rät linje: ingen specifik kurvatur kan omfattas av hur många
olika ellipsbågar som helst (eller andra kurvformer): MED BÄGGE ELLIPSAXLARNA
VARIABLA
finns hur många olika
ellipser som helst som kan fånga in två fixa punkter över ellipsernas
gemensamma fasta horisontalaxel. Figuren ovan illustrerar tre typellipser med
tre givna bågpunkter med olika ellipskopplingar: en mDlow punkt
för alla tre ellipser, två punkter för två ellipser, och alla tre punkterna för
en enda.
ITERATIONSALGORITMEN FÖR
TVÅ ELLIPSBÅGPUNKTER MED FAST VERTIKAL ELLIPSAXEL (Neutronkvadratens inskrivna
cirkelradie ½NK) är redan utformad. Vi bör kunna utnyttja denna som bas för en
vidare iteration. Nämligen med uppgiften att finna den tredje bågpunkten
fusionsprodukten från given fusionsagent mDlow och fusionsobjekt mDhigh.
Men det förutsätter att vi får modifiera ½NK-ellipsaxelns vertikala höjd över
NK-mittlinjen (mD=6 elektronmassor). Samt det avgörande att iterationen
på att finna samhörigheten mellan agent, objekt och produkt sker utifrån
Neutronkvadratens egna bestämda mD-värden.
FUSIONSELLIPSERNA HUR: FusEPSprinc
FUSIONSELLIPSERNA hur?
HUR får man fram
ovanstående FUSIONSEXEMPEL
bevisbara exotermiska fusionskoppling mellan Deuterium och Nobelium med
resultat i Lawrencium?
Engagemang. Motivation. TID att OSTÖRT
studera Partituret.
Anledningen till min egen framgång beror
uteslutande på att hela Parken stått öde och tom under lång tid: jag har fått
vandra tämligen ensam här bland alla godbitarna, ljuvligheterna och omfamningarna.
Men det är nog slut med det nu, snart.
Parken är till för alla.
ITERATIONSELLIPSERNA KALKYLKORTET
NUKLIDEXOTERMISKA ELLIPTISKA
ITERATIONER UH 26Apr2020 exempel på tunga nuklidgruppens exotermiska fusionsbildning
med hjälp av [DEN MODERNA AKADEMINS TEORETISKT OMÖJLIGA] lätta nuklidgruppens
[lämpliga] fusionsagenter PRIMÄRA GRUNDÄMNESBILDNINGARNA I K-CELLENS
EXPANSIONSHISTORIA ENLIGT RELATERAD FYSIK: TNED
![]()
FÖRKLARING exotermiska
kärnreaktionslagen styr:
Säkra FÖRST GARANTI för att en exotermisk
fusion genom (kalkylkortet för) EXOTERMISKA FUSIONSLAGEN alls är möjlig: Endast
om fusionen är möjlig (OK) finns en ellips som förenar komponenterna. Annars
inte.
DEL AV DET NUMERA Apr2020
HELAUTOMATISERADE KALKYLKORTET TILL
EXOTERMISKA FUSIONSLAGEN:

Tabell2 (och 3) innehåller alla 3179st
LBL-nuklider (LBL2003) med angivna atomvikter huvuddelen av dem är av typen
instabila. Den tidigare (1967) HOP-tabellens drygt 1200 isotoper (stabila +
instabila) uppvisar endast marginella numeriska avvikelser. Typformen för dessa
kan också studeras i jämförelsen mellan HOP och CODATA i särskilt diagram. En
särskild liknande jämförelse LBL/HOP kräver en (relativt, manuell) omfattande
insättning av de drygt 1200 HOP-objekten kontra de 3179st LBL objekten, vilket
arbete ännu inte har färdigställts stickproven visar obetydliga differenser
typ
6C16HOP=16.014700 mot
6C16LBL=16.014713.
(som också beror på valet av värden
för neutronmassa, elektronmassa och atomära massenheten här u = 1,66033 t27 KG; dessa varierar
marginellt i vilket fall beroende på epok och tabellkälla: jämför de 6 något
olika u-värdena i HOP).
CODATA ¦ Jämförande
diagram CODATA/HOP
MATA SEDAN HELT ENKELT IN respektive nuklid
med LÄTTASTE (A1=1-60) överst och TYNGSTA (i princip alla möjliga
tabellupptagna A=A2 större än eller lika med A1) underst i ITERATIONSKORTET:
Kalkylkortets cellkoder använder sedan LBL-datat och letar upp respektive
nuklid, dess angivna atomvikt (U) och masstal (A); Atomvikten U räknas om
automatiskt till atomär massdefekt (mD) enligt Neutronkvadratens
anvisningar (Neutronkvadratens härledning, grundsambanden);
En ITERATIONSALGORITM nedan tar fram
den fusionstangerande ellips som skär de givna nuklidobjektens mD-värden
via deras angivna A-värden vilket bevisar samhörigheten via Neutronkvadratens
grundsamband:
NEUTRONKVADRATENS
ELLIPTISKA ITERATION:
Vi
ser endast till den orangea texten i rutan nedan det övriga utvecklades först
med unik giltighet endast inom lätta gruppen (Amax=60), den delen kan inte
användas heltäckande.
a0 = (A
K)/E

BESKRIVNING:
Vi utnyttjar K1 för att iterera fram ett
K1=K2;
Beräkna varje nytt E från K1 på masstalet från A2 och mD2 enligt
NyttE1 = ABS((K1 A2)/[nD2 + TECKEN(A2 60)·60]) FÖRKLARING:
»FEJKA K2 på K1» för att »få syn på» var K2 hamnar med K1:s referens
resultatet blir att K2 närmar sig K1, hur man än räknar. Fortsätt så för
varje nytt varv tills (K2=K1) slutresultatet inte ändras mer i valt antal
decimaler.
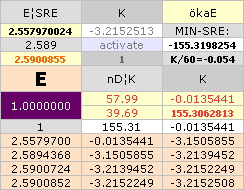
Färdigt.
ELLIPSENS UPPRITNING genom mina egna utformade Delphiprogram vars utvecklingsmiljö Microsoft slutligt har stängt vägen
för användning av (2016+) med (den djupt förnedrande påtvingade
datorockuperande) lanseringen av Windows10 vi väntar på tillfället att få
returnera Den Eminenta Företagsamheten i motsvarande uppvisad ödmjukhet:
GrafEPS EX: Md=120
(1[([x+0.054]/2.59)1]'2)'0.5
Neutronkvadratens elliptiska vertikalaxel
är konstant Neutronkvadratens längd för hela komplexet (mD-skalan med
max 18 elektronmassor med en resterande möjlig negativ del på minus 6).
HELA ellipsen ritas upp
![]()
via
övre delen
+(1[([x+0.054]/2.59)1]'2)'0.5
och undre delen
(1[([x+0.054]/2.59)1]'2)'0.5
ITERATIONERNA MANUELLT »pionjärerna»
Under
utvecklingsarbetet (Apr2020) användes först den helt enkla »anordningen»
CELLKOD:
OM(TECKEN(K1K2)=1;"ökaE"; "minskaE");
Med
generell början på E=1 »ges information om hur nästa steg ska utföras» t.ex.
(lämpligast) E=2;
Är
inslaget E för stort meddelas »minskaE».
Och: Efter idogt petande når man svaret (rätt snabbt). Men hur går Det till?
Jättekul uppgift.
Utformningen i ITE-delen testades först med cellkoden under E¦SRE (refererar
fejkberäkningen på K2): Med E=1 från start »presenteras» nästa lämpliga E:
Man matar in det värdet, och E¦SRE ger ett ännu mera närliggande nästa
inmatningsvärde. Och så vidare. Slutresultatet är detsamma som i (hela
uppställningen) den orangea ITE.
ACTIVATE (1aktiverad, 0 avställd) stänger
för eller öppnar iterationsleden (0 för att slippa se irrelevanta
meddelanden typ gapiga VÄRDEFEL! under utvecklingsarbetet).
Apr2020
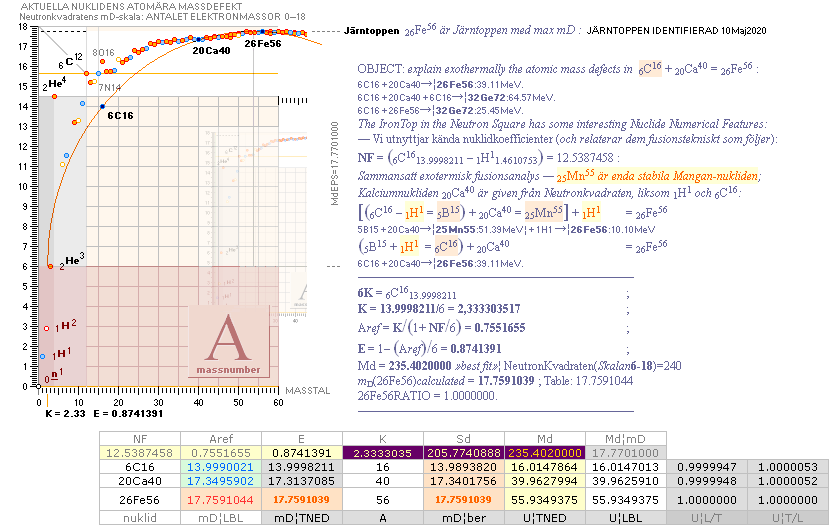
Separat fusionsanalys
en del av komponenterna
5B15 = 2He6 + 1H3 + 2He6
2He6 + 1H3 + 2He6→¦ 5B15:20.99MeV.
= (2He6 + 3Li8 = 5B14) + 0n1
3Li8 + 2He6→¦ 5B14:14.75MeV
¦ + 0n1→¦ 5B15:2.74MeV.
2He6 = 21H3
1H3+1H3 →¦ 2He6:12.20MeV.
3Li8 = 1H3 + 1H2 + 1H3
1H3+1H2+1H3 →¦ 3Li8:21.9MeV
.
MeV = minstEXOTERMISKT AVGIVEN FUSIONSENERGI i MegaElektronVolt: E=UQ; E/Q=U; (E/e)/T6 =
MeV.
Det var det
intressanta: det fanns en koppling.
Alternativ som först
framkom vid prövningen:
Problemnötterna med
att finna fusionsanalysens parametrar för K, Aref och NuklidReferensen NF.

KURVSKARAN 6C16: FusionsEPSmetod
6C16 FUSIONSELLIPSERNA I
NEUTRONKVADRATEN
Hur
vi finner atomära massdefektsvärden
atomvikterna för exotermiska fusionsprodukterna
Enkla iterationsellipserna:
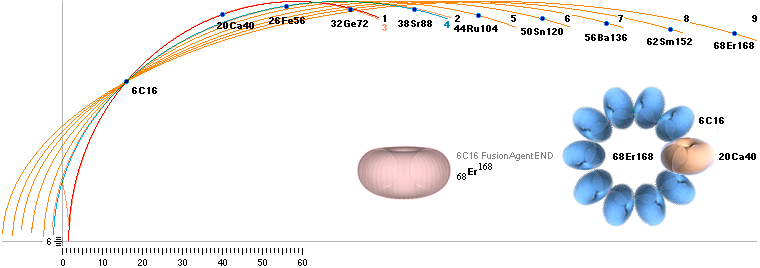
Enkla
ITERATIONSELLIPSERNA OVAN med
resultatdata från beräkningarna: U = Amn(1 mDme);
Sammansatta tabellformer på givna
cellresultat
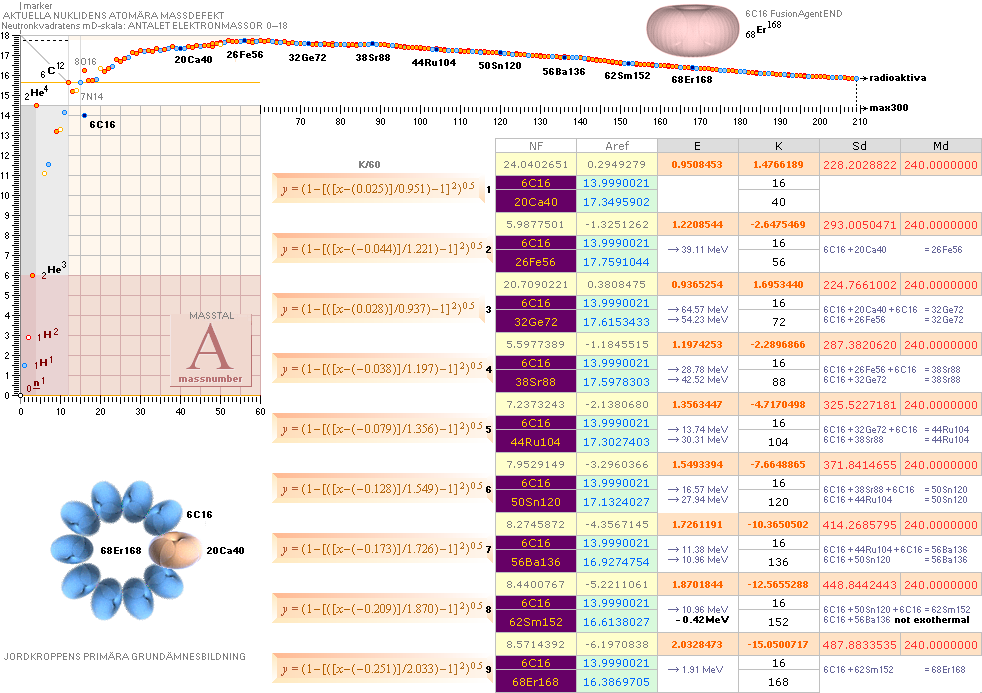
1
och 2: NK-mD-bestämda 6C16 och
20Ca40 NK- beräknar mD för 26Fe56 mD
= 17.7098627;
3 : NK-mD-bestämda 6C16 och
20Ca40 NK- beräknar mD för 32Ge72 mD
= 17.5531404;
4 : NK-mD-bestämda 6C16 och 26Fe56
NK- beräknar mD för 38Sr88 mD
= 17.5419545;
5 : NK-mD-bestämda 6C16 och
32Ge72 NK- beräknar mD för 44Ru104 mD
= 17.1940036;
6 : NK-mD-bestämda 2He4
och 32Ge72 NK- beräknar mD för 50Sn120 mD = 17.1480771;
Ingen definierad skärning finns med
ett fusionsOBJEKT.: närmast 28Ni64. [via2He4].
Det finns en ellipsväg via 2He4
och 26Fe56. eDIFFmD större med 0.0156744
7 : NK-mD-bestämda 2He3
och 32Ge72 NK- beräknar mD för 56Ba136 mD = 16.9642150;
Samma här: Närmast mD17.6: 29Cu67 eller 30Zn67 mD17.625
Funnen via 2He3 och 32Ge72, ELLIPS
2He3 + 56Ba136 visar skärningen direkt.
STÖRRE än tabellvärdet med
0.0367396.
8 : NK-mD-bestämda 6C16 och 32Ge72 NK- beräknar mD för 62Sm152 mD = 16.6774799;
Den går, skärs av 32Ge72.
STÖRRE än tabellvärdet med
0.0636772.
9 : NK-mD-bestämda 6C16 och 32Ge72 NK- beräknar mD för 68Er168 mD = 16.3411658;
Också denna skärs av 32Ge72 va en
ellips med LITET större vertikalvärde än ½NK: 240.9289960.
eDIFFmD=0.0458048;
Exotermiska
Fusionsagenten 6C16 slutar på
fusionsprodukten 68Er(Erbium)168. För att komma vidare till ännu tyngre atomer
måste en annan fusionsagent anställas, en med lägre massdefekt.
HAVSGRÖNA
KOLUMNvärden anger tabellverkets (här LBL)
![]()
atomära
massdefektsvärde (mD) beräknat från tabelloriginalets atomviktsvärde (U)
enligt mD = (1 U/Amn)/me med
U atomvikten i atomära massenheter (här
1u = 1.66033 t27
KG)
varierar marginellt (här helt utan betydelse) mellan olika tabellverk
A masstalet
antalet primära neutroner (konv. protoner och neutroner) som atomen
bildats av
mn neutronmassan (här 1.0086652u)
me elektronmassan (här 0.000548598u)
Det
faktum att neutronkvadratens ellipser nära men inte exakt skär dessa värden
ger i sig en (inledande) stark indikation på samhörigheten: Experimentalfysiken
+ TNED = sant.
EFTERFÖLJANDE
ANALYS använder de så approximativt givna fusionsellipserna för att mera
noga, exakt och precist ta fram Neutronkvadratens egna exakta mD-värden
ur de redan tidigare och föregående givna. Se särskilt från GRUNDNUKLIDERNA.
Dessa skiljer sig så litet från experimentellt uppmätta värden att
differenserna tangerar området för massökningseffekter i den masspektroskopiskt
uppmätande apparaturens referens. Se särskilt 2Helium4-differensen i Jämförande
Grundnuklider.
GRUNDNUKLIDERNA ¦ Jämförande Grundnuklider ¦ ELLIPSITERATIONERNAS HÄRLEDNING ¦
Här
avslutas framställningen i ämnet TUNGA NUKLIDGRUPPENS FUSIONSELLIPSER
Vi har gett en del exempel med jämförelser
på hur atomära massdefekter kan itereras fram ur TNED-fysiken.
Editor22Nov2020
Partierna
nedan som följer ger främst kopplingar till fusionsnuklidernas möjliga status i
samband med primära Jordkroppens bildning, enligt TNED-kosmologins anvisningar.
Se särskilt från IronCORE.
Utvecklingen: NuklidTab4.wks2003 ¦
INRÄTTNINGAR SOM
HINDRAR OCH FÖRSTÖR FÖR KUNSKAPSUTVECKLINGEN: Microsoft 2015+ börjar diktera användningen av den tidigare
valda egna inköpta datorn ..
»Du
vill inte veta» vilket stundtals helt onödigt Microsoftpåtvingat h-e:
Webben blir
också allt svårare att konsultera
(Apr¦Sep¦Nov2020): En del naturvetenskapliga webbsidor har börjat stänga till
helt och hållet för insyn om man inte accepterar anslutning till COOKIES.
4Nov2020: Google&Microsoft låser alla internetsidor om man
inte medverkar i cookies.
1.
Var och en har rätt att äga egendom
ensam såväl som i förening med andra., A17.1;
2.
Ingen får självsvåldigt berövas sin egendom., A17.2.
ASSOCIATIVT TÄNKANDE MED KUNSKAPSUTVECKLING
SOM UTFÖRS MED HJÄLP AV SKRIVMASKIN OCH BILDBEHANDLINGSVERKTYG SOM INKÖPTS
FÖR EGNA MEDEL ÄR PRIVAT PERSONLIG INDIVIDUELL EGENDOM SOM UTOMSTÅENDE INTE
HAR MED ATT GÖRA. VARFÖR KASTAR INTE VÄRLDSSAMFUNDET UT MICROSOFT 2020 OCH
LÅTER, TILLÅTER, MÄNSKLIGHETEN ATT FÅ UTVECKLA SIG SJÄLV UTAN INTRÅNG, UTAN
DIKTAT, UTAN INSYN OCH INBLANDNING FRÅN MICROSOFT? WhatsUp?
Lätta nuklidgruppens stabila isotoper
upp till atomnummer 29 ¦ masstal 59 se särskilda fönsterdumpar
NuklidTab4.wks2003 som har kiopierats med resultatbilden här i efterhand
(22Nov2020) från en Windows XP-dator.
Microsoft har tagit bort det enda
kalkylprogrammet MsWORKS 4.0 som kan presentera cellkoderna i exakt
överensstämmelse med redan kända atom och nukliddata: får inte visas för
allmänheten, enligt Microsoft. Företaget samarbetar inte med enskilda.
EXCEL och OpenOffice + associer4ade
demolerar kan inte översätta, transponera originalet heller UTOM till
oigennkännelighet.
Kan inte användas för uppgiften.
Varför framstår MsWORKS 4.0
Kalklylprogram som suveränt inom relaterad atom och kärnfysik? Programkoden
för VILLKOR är logiskt korrekt.
Microsoft förbjöd stängde ner
hela den programformen efter en uppdatering som företaget vägrade återkalla (WindowsVista 2008).
KALKYLKORTEN
GENERELLT i UniversumsHistoria
alla de som
utvecklades först i MsWORKS 4.0 är inte av den mera komplicerade art som
exemplet ovan (NuklidTabell4.wks). Dessa (av den mera enkla arten) kunde därför
utan större äventyr översättas till OpenOffice-versioner (med vissa äventyr)
och därmed integreras med huvuddokumenten. Se
KALKYLKORT
ALLMÄNT OM ÖPPNINGSMANUALEN i Register.
Exemplet
med lätta nuklidgruppens atomer ovan understryker ett allmänt allvar, och
ansvar, i kunskapsutvecklingen som speciellt affärsrörelser och deras ansvariga
ägare verkar ha väldigt svårt med, som det har visat sig.
NEUTRINOSPEKTRUM OCH
PRIMÄRFUSIONERNA, enligt TNED:
AVGÖRANDE
VIKTIGT FÖR LÄSAREN ATT KÄNNA TILL
ALLMÄNNA GRUNDSATSER INOM DEN
RELATERBARA (TNED) KÄRN- OCH ATOMFYSIKEN
PLANCKS
STRÅLNINGSLAG BEVISAR EN PLANCKS STRUKTURKONSTANT som inte uppmärksammats
inom den moderna akademins kvarter: begreppet om en osäkerhet för VARJE fraktal
Planckringsnivå h=mcr. Inte enbart den yttersta.

LJUS ÄR INTE GRAVITATION = massa. Säg det åt
Modern Akademi. Icke sa Nicke. I FEEL you.
I
sammanfattande utdrag från originaltexten neutrinospektrum illustrerat
Eftersom
detaljerna är helt orepresenterad i moderna kvarter, är det avgörande viktigt
att läsaren känner till dessa följande ytterst viktiga och delvis »enkla»
grunder. I annat fall missas hela insikten.
NEUTRINOSPEKTRUM ¦ Energilagen ¦ Neutrinostrålningens grunder ¦ Planckringen ¦
Samma
sak uttrycks mera avancerat i ENERGILAGEN.
Eftersom massans vägande struktur således
inte kan skapas, och elektronen HAR vägande massa som utvecklar
centrifugalkraft (se trådstråleröret), är det tydligt att elektronmassan måste
härröra avdelas från (och åter kunna upptas av) atomkärnan.
Eftersom massa inte kan skapas är
elektronens vägande massa en fundamentalt avdelad beståndsdel av
atomkärnan (neutronen).
ENERGILAGEN gör Det alltså klart redan från grunden.
I modern akademi finns inte begrppet
struktur för Plancks konstant (se Plancks strukturkonstant) varför heller ingen
uppfattning KAN finnas om elektronmassan som bestående av mindre element och
som i sin tur härrör just från atomkärnan trots att modern akademi mycket väl
känner till att elektronen ligger utspridd kring atomkärnan. Allt återfaller på
Q den elektriska laddningens härledning och som modern akademi garanterat
inte kan härleda. Se utförligt från elektriska laddningen.
Beskrivning
objekt:
E = hf
= (m→γ)c2
I
TNED ÄR PLANCKS KONSTANT EN STRUKTURKONSTANT Neutronen (N3m20): Planckringen h=mcr
Eftersom
elektronspektrum är lika för alla atomer (betasönderfallen) men inte
neutrinostrålningen (som »bygger upp» atomkärnornas struktur genom fusioner
från lättare till tyngre), KAN massekvivalenta elektronenergier sönderdela alla
atomkärnor enligt det kvalitativa sambandet E = hf = (m→γ)c2
= (m←γ)c2. Samma kvantitativa
sönderdelningsenergier, nämligen, som bildas från fusionerna garanterar att
energierna som frigörs med bildandet av de tyngre atomkärnorna INTE
sönderbryter de lättare atomkärnornas byggnad. Neutrinoenergierna som
sammanhänger med atomkärnornas bildning, bildar TVUNGET olika fraktala nivåer i
atomkärnan (se från Planckringen), och dessa är inbördes säkrade genom
att de högsta neutrinofrekvenserna tillhör de lättaste atomkärnorna så att
dessa inte sönderdelas på de tyngres bildning. Om energin vore elektronhomogen
också för kärnfysiken, vore (alltså) de olika atomkärnorna en omöjlighet.
kärnspektrum
Atomkärnans
fraktala frekvens och våglängdsspektrum i TNED
Betrakta
![]()
Om n1 motsvarar den djupast
liggande fraktalnivån, motsvarande den lättaste atomkärnan, n2
den närmast högre liggande fraktalnivån motsvarande den närmast högre liggande
nuklidbildningen, osv, ges en frekvenskarta exakt motsvarande
nuklidbildningarna där frekvensen avtar från lättare till tyngre, analogt
fusionsvåglängden är växande med tyngre nuklider. n-suffix med högre
heltal motsvarar då atomkärnor med högre atomvikt: Fusionsfrekvenserna spärrar
kvalitativt mot varandra så att frekvenserna från tyngre nuklider (längre
våglängder) inte åstadkommer en sönderdelning av frekvenser från lättare
nuklider (kortare våglängder).
Med ovanstående ekvivalent vinner man den
excellenta fördelen, att en energiekvivalent (E=hf) alltid kan bildas
kvantitativt genom (artificiellt genererade) elektronsvängningar, vilka ju
gäller lika för alla atomer och för ändamålet att exakt kunna fejka en
nukleär uppdelning av vilka som helst nuklider i deras komponenter genom att
låta en nuklid bada i sin egen kvantitativa fusionsenergi (m→γ)
= (m←γ).
Nukliderna själva har under
nuklidbildningarna ingen sådan finess, eftersom frekvenserna i den
naturbaserade grundämnesbildningen alstras av kärnan (se Grundämnesbildningen,
Nuklidbarriären).
Inte höljet.
Den lägsta frekvensen (tyngsta nukliden)
har tvunget kortare våglängd än elektronelementet, vilket spärrar för
elektronkopplingar som i annat fall skulle överföra fusionsenergierna i ett
blandat kvantitativt tillstånd, tillämpliga på alla atomkärnor, och därmed
effektivt krossa hela byggnaden.
Därmed bevaras fusionsfrekvenserna säkert
separerade i de lokaler där de termonukleära fusionerna utlämnas åt sig själva
genom naturliga processer. Högre nuklidbildningar äventyrar inte de lättare
komponenternas hållfasthet, vilket skulle vara fallet om fusionsfrekvenserna
vore helt kvantitetsgrundade.
Därmed säkras grundämnesbildningen i samma
termiska lokal med samtidig existens av lättare och tyngre nuklider oberoende
av temperaturens magnitud. Fusionerna kan alltså friska på bäst de vill med
avgivandet av termiska bidrag via massdefekterna. I och med, nämligen, att
dessa med allt tyngre nuklider förknippas med allt längre fusionsvåglängder,
gynnas rörelseenergin för de lättare omgivande (på kortare våglängder baserade)
nukliderna. Därmed kan också rejält höga temperaturer bildas (lokalt) som följd
av fusioner från lägre till högre masstal.
Om man alltså artificiellt försöker att
härma den naturliga, självutlämnade proceduren, kommer man grundligt att
misslyckas med det, eftersom den enda artificiella svängningsgenerering som
finns att tillgå är den som gäller lika för alla atomer. Nämligen den som
ombesörjs av elektronsvängningar, analogt Plancks STRUKTURKONSTANT h på
dess högsta fraktalnivå (No1).
Vad man med ovanstående energiekvivalent
följaktligen kommer att finna i sådana experiment, blir just det att en
strålenergi som kan sönderdela en viss atomkärna enligt E=hf, samtidigt
också kan sönderdela samtliga lättare typer enligt ekvivalenterna
![]()
Betasönderfall
däremot hämmas generellt lika för alla atomer eftersom alla atomer i det
avseendet grundas på exakt samma komponent: elektronen (vidare nedan i
Grundämnesbildningen).
OBSERVERA att våglängdsbildningarna för
atomkärnorna via neutrinospektrum INTE är analoga med den motsvarande
konventionellt benämnda s.k. de Broglies vågekvation (λ=h/mv) där
våglängden avtar med växande masstal. I TNED är sambandet λ=h/mv en
interatomär elektromekanisk energiöverföringsform (MIC, mass interactive
connection) mellan mekaniska och elektriska fenomen (jämför
neutrondiffraktion), ingen beskrivning av materiens eller massans byggnad.
Neutrinofrekvensernas n-suffix beror
på fraktalsystemets matematiska delning, och den algoritmen är enligt TNED bara
känd i detalj för första underfraktalen enligt N3m20-aggregatet.
Neutrinospektrums fraktala delning kan alltså fastställas av princip, ehuru (ännu
2007-01-22) inte i någon annan detalj än den som sammanhänger med atomvikternas
inbördes relationer. Se vidare i NEUTRONKVADRATEN.
MIC ¦ Plancks Strukturkonstant ¦ N3m20-aggregatet ¦ Neutronkvadraten ¦ Grundämnesbildningen ¦ Nuklidbarriären ¦
Planckringen ¦ Elektriska laddningen ¦ Elektriska laddningens härledning ¦ Energilagen ¦ Neutrinostrålningens grunder
Comptoneffekten illustrerad:
Neutrinospektrum
INTERVALLETS
OFÖRSTÖRBARHET ¦ Atomtriangeln ¦ Zenons
Teorem ¦ PASTOM massans
principiella struktur ¦ Comptoneffekten
COMPTONGRÄNSEN ¦ Elektriska
Kraftlagen
ATOMKÄRNANS toroidkroppens EKVIVALENTA GEOMETRI VID
DEFORMATION ¦
PLANCKS
STRUKTURKONSTANT KOPPLAR DIREKT TILL ATOMKÄRNANS INKOMPRESSIBILITET
Atomkärnan står redan på noll
√
F/k = Q/r = (Q/[n→ ∞])/(r/[n→
∞]) = Q/r elektriska kraftlagen
ATOMKÄRNANS
INKOMPRESSIBILITET den moderna akademins fatala kosmologiska grundfel
ENERGI arbete E=mad kan varken
skapas eller förintas, endast omfördelas:
ett yttrsta upphov till
massbegreppet kan inte relateras:
FÖRESTÄLLNINGEN OM ETT KOSMOLOGISKT
ÄNDLIGT MASSINNEHÅLL KAN INTE RELATERAS: Stjärnor förbrukar massa genom
omvandling till värme och ljus: OM massa AV PRINCIP vore ändlig har
stjärnfysiken för eoner sedan upphört: vi VET att så INTE är fallet.
sammanknyter och relaterar helheten
PASTOM
massans principiella struktur i utdrag
Massförstörelsen
kräver en i massan inneboende struktur
massa består av ett obegränsat antal
masselement som oupphörligen delas så att någon minsta massdel inte kan
återfinnas
m = m(n→∞)(n→∞)1
= (F/a)(n→∞)1(n→∞) =
(F/[a(n→∞)])(n→∞) = m(n→∞)
n→∞, n växer obegränsat, »n går mot
oändligt»
[Mass-fractal
clause, MAFACE].
Bevis:
PASTOM ¦ GRIP ¦ DEEP ¦ E=mc² = hf divergensenergin ¦ PASTOM ¦ PASTOM ¦ PASTOM ¦ Energilagen ¦ Atomkärnans
g-härledning ¦
Potentialbarriären ¦ Plancks Strukturkonstant ¦ TNED ¦ PLANCKRINGEN ¦ GRUNDÄMNENAS PERIODISKA SYSTEM ¦ Kärnradierna ¦ Kubgrafen ¦
Neutronkvadraten ¦ Spektrum och Kvanttalen ¦ Allmänna Gaslagen ¦ N3m20 ¦ Härledningen
till N3m20
Energilagens
andra huvudsats utpekar en primär massförstörare. Denna härleds i ljusfysikens
och elektricitetens princip (DEEP) som den redan kända E=mc2.
Dess giltighet för massans fullständiga upplösning kräver en i massan
inneboende struktur vars allmänna massform leder till den sekundära
massförstöraren eller rörelsestrukturen mc2=Jf,
beteckningen J för impulsmomentet generellt. Den definieras sedan vidare i
PASTOM genom olika följdsatser.
Den inneboende tillämpningen av GRIP på
PASTOM, m=(F/[a(n→∞)])(n→∞),
leder till den fundamentala massformens definition genom gravitationen på
ringens eller toroidens fraktala form (J=mv·2πr). Massformen
består tydligen av eller får så tydligen förstås bestå av en principiell
ringform vars underfraktaler av m växer obegränsat på m med en
motsvarande växande tyngdkraftsacceleration (Atomkärnans gravitella
härledning). Massformen, med den enligt Potentialbarriären omgivande
laddningen inkluderad, beskrivs därigenom som en av gravitationen bestämd och
enligt energilagen utan upphov befintlig kraftväv med omgivande elektriska och
magnetiska fält motsvarande fraktalernas struktur. Alltså, ett elektromekaniskt
toroidaggregat av utomordentlig sammansättning där masstätheten växer med
djupet i fraktalstrukturen utan slut (Plancks strukturkonstant Atomkärnans
gravitella härledning). Aggregatets allmänna dynamik behandlas i TNED (Toroid
Nuclear Electromechanical Dynamics). Den fundamentala massformen motsvarar
naturligt grundämnenas mest elementära beståndsdel vilken vi identifierar med atomkärnan
(PLANCKRINGEN). Genom att jämföra toroidformens relativa dimensioner mot Kubgrafen
(se Kärnradierna) kan geometrin (N3m20) för det aktuella primära
toroidaggregatet (neutronen-protonen) bestämmas.
Kärnradierna: Neutrinospektrum
Den centrala masstruktursatsen, som
formulerad ovan[], leder
direkt på Kubanalogin som grundlägger den mera reguljära härledningen till
atomens dynamik härledningen till GRUNDÄMNENAS PERIODISKA SYSTEM genom
Keplermomenten och Kärnsyntesen genom upptäckten av NEUTRONKVADRATEN.
Keplermomentet tillhör grundfysiken från Fysikens 7 Principer (NEONS)
och beskrivs särskilt i grundämnenas periodiska system.
Med kännedom om den elementära vågmekaniken
(studiet av vågrörelsernas utbredning genom främst vatten och enkla anordningar
[rep]) och det allmänna impulsmomentet för atomen på dess grundnivå (h,
Plancks konstant) framträder Spektrum och Kvanttalen med (grundkartan till)
Grundämnenas Periodiska System i en separat del. Nämnda delar härleds då
tillsammans med övriga från mekaniken kända grundbegrepp i former som mera
ingående beskriver och förklarar atomkärnans delar. Därefter följer slutligen
hela Termodynamiken (i vid mening): beskrivningen av himlakropparnas uppkomst
med deras och alla övriga alla materials egenskaper och tillstånd (primärt från
Allmänna Gaslagen). I allt: elementär grundfysik som tydligen inte
imponerat på modern akademisk intelligens: ingår inte.
NEONS ¦ Den elementära vågmekaniken ¦ LISTAN ¦ noMACfysik ¦ MAC, här
ofta använd förkortning för Modern ACademy
Explicit
således elementär grundfysik
ATOMKÄRNANS
INKOMPRESSIBILITET atomkärnans formbevarande kraft
Atomkärnan är redan »maximalt tät» inte
genom volym utan genom YTA: toroidfraktalernas natur;
Atomkärnans yta är »super ultra enormt
kanon» HÅRD. Hårdare finns inte: gravitationen av princip.
Gravitationens fundamentalform atomkärnan
kan inte göras tätare än den redan är: neutronen+.
Den populära sensationella moderna
akademins SVARTA HÅL masskroppar med av modern akademisk princip
»oändlig massa» inom »oändligt liten sfär» är en (populär) vanföreställning:
fysiken innehåller ingenting sådant.
DÄREMOT ljusets gravitella beroende (se Exempel
på »Svart hål» i Relaterad Fysik) finns en zongräns där c=0 utanför
en tillräckligt stor kvantitet massa som är innesluten av en tillräckligt
lämplig sfärisk volym.
ATOMKÄRNANS INKOMPRESSIBILITET ¦ ATOMKÄRNANS toroidkroppens EKVIVALENTA GEOMETRI VID
DEFORMATION ¦
Hur
det konventionella begreppet svart hål motsvaras i relaterad fysik ¦
GB: Kärnradierna
TNED basics
GRUNDÄMNESBILDNINGEN
ATOMKÄRNANS INKOMPRESSIBILITET ¦ Den tunga nuklidgruppens certifiering ¦ Nuklidbildningarna ¦ Atomkärnans
1818 + 18 + k centralmassiv
EXOTERMISK som ger ut arbete =
värme och ljus
ENDOTERMISK som KRÄVER arbete
Förutsättningen
för fullständig EXOTERMISK grundämnesbildning
från neutronen med masstalet 1 till atomkärnorna med de allra högsta, fysiskt
möjliga masstalen, enligt TNED max 317 (förenklat »max 300»), f.ö. den moderna
akademiska kosmologins stora olösta svåra fråga[]
är en
snävt tidsbegränsad tillgång på (starkt) betaaktiva »neutronpumpade»
nuklider: TNED, relaterad fysik, utpekar de främsta »neutronpumpade»
fusionsagenterna:
![]()
![]()
![]()
![]()
Varför då?
Alla atomer ZnamnA med sina nuklider över Järntoppen, här den s.k. tunga
nuklidgruppen, kräver allt flera ekvivalenta ursprungliga neutroner (n)
än protoner (p) för att bibehålla en stabil kärnstrukturell
balans
(nuklider som är stabila gäller upp till Bismut sv.
Vismuth 83Bi209 alla tyngre atomer är radioaktiva). Motsvarande
ordning i lätta nuklidgruppen är att (nästan) alla nuklider har samma masstal (A=n+p)
som atomnummer (Z), typ 14Kisel28 frånsett sådana som de 4 ovan
exemplifierade som sönderfaller i kärnytan till atomer med högre Z-tal; De
gör så genom att bygga/autonomt balansera ut formstabilisera
atomer med motsvarande (ur kärnytans neutrala ±e-väv) utgivna antal
elektroner som alltså automatiskt kopplar motsvarande kärnstrukturellt
»upphöjda» positroner; exakt elektrisk balans mellan kärna (+) och hölje
().
Dessa
har emellertid begränsad användningstid och sönderfaller (i
kärnytorna till atomer med högre atomnummer) allt snabbare ju mera
neutronpumpad nukliden är. Det är anledningen den begränsade tiden
varför teorin i modern akademi brottas (förgäves) med den kosmologiska
huvudfrågan HUR alla tyngre grundämnen än de runt Järntoppen har kommit till.
Jämför TNED:
AVGÖRANDE
VIKTIG GRUNDFYSIK: originalförfattning 2007XI27
Utdrag
från Nuklidbildningarna DEN TUNGA
NUKLIDGRUPPENS CERTIFIERING
Certifieringen
för de tunga nuklidernas bildning K-cellens expansion; primärkropparna
GRUNDÄMNESBILDNINGENS
KÄRNA
Neutrinostrålningen
och de betaaktiva nuklidernas bevarande
NEUTRINOSPEKTRUM ¦ Energilagen ¦ Neutrinostrålningens grunder ¦
(m→γ),
»massa till gamma» generaliserad TNED-beteckning för
massdestruktion eg. från neutrino- till lägre frekvenser [närmast gamma]
m→γv originalförfattningens neutrinorelaterade
exotermiskt utgivna fusionsenergigrund, här förenklat generellt (m→γ)
ORIGINALFÖRFATTNINGEN
I WORD MED TECKENSNITTET SYMBOL = GREKISKA ALFABETET Ctrl+Shift+Q FÖR
NATURVETENSKAPLIGA TERMBETECKNINGAR typ p för PI och g för GAMMA osv i den då
[1994+] dominerande webbläsaren INTERNET EXPLORER, huvuddelen av alla
UH-dokument och man trodde att den teckenstandarden skulle fortsätta. Så
skedde inte. En del webbläsare [successivt
2010+: internet explorer minskar i användning, andra webbläsare introduceras]
läser inte teckensnittet Symbol vilket i princip gör originalförfattningarna
här oläsliga [UNICODE-STANDARDEN HAR ETT
SÄRSKILT »SYMBOL» FÖR VARJE TECKENSNITT, MED RESULTAT I EN GARANTERAT UTSPRIDD
ICKE ENHETLIGT KVALITATIV TECKENSNITTSBUTIK: STUNDTALS YTTERST SVÅRNAVIGERAD I
AVANCERAD MATEMATISK PRESENTATION, LÅNGT IFRÅN DET ENHETLIGA SUVERÄNA SYMBOL: man
får leta, leta, leta .. om alls: enhetligheten har vandaliserats fullständigt
totalt 100%: 100% förstörd arbetsro. DEN MODERNA AFFÄRSVÄRLDENS FÖRETRÄDEN
ÄR EXPERT PÅ ATT BRYTA NER NATURVETENSKAPLIGA GRUNDER: Rätta gärna om fel. Det
vore underbart].Microsofts och GOOGLE CHROMEs senare löpande mer eller
mindre självmord på den egna webbläsarens läsbarhet för små teckensnitt
praktiskt taget oläsligt från runt 2015+ men fortfarande med läsbarhet på
Symbol har »korrumperat och infekterat» hela INTERNETKOMPLEXET: tidigare
användbart har förvandlats till ett rent h-e FÖR
DEN SOM INTRESSERAR SIG FÖR ENKEL TYPOGRAFISK FRAMSTÄLLNING PÅ TRADITIONELL
NATURVETENSKAPLIG SKRIVBAS: användbarheten arbetsron 2015+ i stadigt minskande, mer och mer instängt och
underkastat GOOGLES och MICROSOFTS världsmonopoilistiska användardiktat.
INTERNET
GENERELLT Apr2020: Klarar inte ens av att recitera VISA UTAN ATT FÖRVANSKA
ORIGINALET en BOKTEXT PÅ TRADITIONELL NATURVETENSKAPLIG TECKENSTANDARD:
SYMBOL. Sänk Internet. Helt. Så fint och lovande från början.
Totalförstört för kunskap 2020.
DET GÄLLER
ATT FAVORISERA OCH VÄRNA OM ARTRIKEDOMEN: ta bort så mycket som möjligt.
Strömlinjeforma Individerna.
NEUTRINOSTRÅLNINGENS
ALLMÄNNA BETYDELSE för fusionerna beskrivs i separat artikel i samband med
beskrivningen av atomkärnans allmänna struktur och Plancks konstant. Se
NEUTRINOSPEKTRUM, om ej redan bekant.
För
att fusionsbildningen i den tunga nuklidgruppen (från runt A=60 och uppåt) ska
fungera genomgående på exotermiska fusioner, krävs ENLIGT TNED en förekomst av
tillfälligt varaktiga neutronrika betaaktiva nuklider, Betaagenter. Det
är mjukt instabila atomkärnor som bevarar kärnans ursprungliga
neutronsammansättning men kan ändra kärnladdningen. Normalt sett sönderfaller
betaaktiva nuklider i kärnstrukturen men inte i kärnformen, och tappar därmed
delar av utfyllnadsmassan i 18e-stocken som höjer nuklidens massdefekt.
Fusionsfasen är visserligen i sig kortvarig (min
t22 sekunder, se FUSIONSTIDENS
BERÄKNING). Men det är ingen garanti för att normalt sönderfallande
betaaktiva nuklider ska hinna fusionera i ringen innan de sönderfaller.
Eftersom ENLIGT TNED alla betaaktiva atomkärnor i sina betasönderfall utvecklar
exakt samma neutrinobetastrålning (m→γ) sett till frekvens
och våglängd, är det tillräckligt om Betaagenten får »bada» i
neutrinobetaEkvivalenten (m→γ) för neutronens sönderfall
enligt energiekvivalenten
(0n1)
= 1H1stabil + (m→γ).
Den betaaktiva nukliden hålls då på en exciterad energinivå och inget
betasönderfall sker
förrän neutrinobetanivån sjunker under hållvärdet.
ATT
kallplasmatillståndet med fusionsringarna verkligen garanterar Betaagenterna
klargörs på följande sätt.
Fusionstidens
beräkning ¦ Centralmassivet
1818e ¦ Neutronkallplasma ¦ Planckenergin
E=hf ¦ Wiens förskjutningslag
Temperaturekvivalenten
till varje energiekvivalent fås genom Planckenergin
(E =
hf = h6,626 t34 JS c0 2,99792458
T8 M/S /λ) och Wiens förskjutningslag
(λ
= k2,898 t3 M°K T1) enligt sambandet T=kλ1
= E(k/hc0) med T i °K.
EXEMPEL:
I neutronens sönderfall till väteatom ges neutrinoenergin i medelvärde som
E = 0,764
MeV = 1,223928 t13 J; T = E(J)·(k/hc0)
= E(2,898 t3)/(6,62559 t34 · 2,99792458 T8) = 1,7857020 T9.
Temperaturekvivalenten
i exemplet blir: 1,7857 T9 °K. I
konventionell kosmisk mening finner man bara sådana temperaturer i de
allra hetaste av stjärnor[].
Frånsett de okontrollerade vätebomsexplosioner som kortvarigt kan uppnå
temperaturer på runt 10 T9 °K finns alltså och till jämförelse ingen praktisk
möjlighet att genomföra experiment ens med de allra lägsta neutrinoenergier för
kontroll av den betasönderfallshämmande neutrinoeffekten. Genom analogier som
berör atomkärnans frivridande moment i samband med fusionskopplingarna, kan man
ENLIGT TNED anställa en jämförande kinematisk analogi som leder till en
motsvarande temperaturekvivalent under fusionsfasen från neutronkallplasmat (Se
samband och figur i Termiska Ekvivalenter). Resultatet ger en
temperaturekvivalent som är omvänt proportionell mot kärnradien. Sambandet kan
då i förenklad mening ställas direkt i relation till masstalet A enligt
uttrycket T=A1/3 T12 °K. Högsta teoretiska masstalet enligt
TNED är A=317 (se Nuklidkartans gränsvärde) som ger ett allra lägsta
T = 1,47 T11 °K. Neutrinobetaekvivalenten i fusionsfasen är därmed
säkerställd med goda marginaler: med A=1 ges ett teoretiskt Tmax = 1
T12 °K; Betanuklidens BetaSönderfall kan vänta tills ekvivalenta
fusionstemperaturen faller under hållvärdet.
Termiska ekvivalenter ¦ Nuklidkartans gränsvärde ¦ Plancks
konstant ¦ Fusionsring ¦ Comptoneffekten
För att neutrinobetaenergins ekvivalent ska
ha någon betasönderfallshämmande effekt under den mycket kortvariga
fusionsfasen, måste neutrinostrålningen avges i omedelbar närhet till
betaagenten (Comptoneffekten garanterar att Planckenergin hf avtar med
strålenergins inverkan på massobjekt). Detta blir också det praktiska
fallet genom varje fusionsring genom att atomkärnorna ligger optimalt nära
varandra. Ringens sekventiella fusioner garanterar att närliggande eventuella
betaagenter bokstavligen kommer att bada i rejält höga (tabellexempel nedan)
neutrinogenererade strålningstryck via massförintelsen (m→γ)
i fusionerna. Därmed kan fusionsfasen dra fördel av full uppsättning nuklider i
hela nuklidkartan utan risk för att några betasönderfall inträffar. Alla,
samtliga möjliga nuklider som bildas genom fusionsringarna, blir
likaberättigade och certifierade fusionsagenter.
Betaagenterna
som krävs för fullständig materiebildning
är 2He6, 3Li8 och 6C16.
Betaaktiva 1H3 figurerar också, men dess normala
sönderfallstid är 12,26 år och är därför inte kritisk i J-kroppens snabba
fusionsfas. Samma gäller också egentligen för agenterna 2He6 och 3Li8 som normalt
sönderfaller efter respektive 0,82 och 0,86 sekunder [VAN
NOSTRANDs SCIENTIFIC ENCYCLOPEDIA Fifth Edition 1976 s491-515, Table 3];
De momentant kortvarigt höga
neutrinoenergierna från de tätt liggande fusionerande atomkärnorna garanterar,
säger TNED, att alla betaaktiva atomkärnor väntar med sina sönderfall tills
hela kroppens fusionsfas är avklarad. Med nuvarande laboratoriestandard i
neutronens sönderfall betyder det; efter max 12-14 minuter. Därefter kan mera
normala nukleära sönderfall ta sin början.
Neutronen upptäcktes år 1932 av Chadwick.
Atom- och kärnfysikens första spännande dramatiska 30 år 1900-1930 (TRETTIO ÅR
SOM SKAKADE FYSIKEN, George Gamow, Prisma).
ironCORE: KROPPSROTATIONEN ¦ ILLUSTRERAT FÖRLOPP ExoEx Järnkärnans allmänna betydelse
4Sep2020 sammanst.
Härledd
konsekvensfysik
JÄRNKÄRNANS
BILDNING INNEFATTAR TYDLIGEN EN SYNTES AV HELA KOMPLEXETS FYSIKFÖRKLARING
JÄRNKÄRNAN hur den bildas i detalj
enligt TNED
TNED-fysikens beskrivning
FRÅN
J-KROPPENS DIVERGENSTÄNDANDE ÖGONBLICK lokala g-potentialen medger ljushastigheter
större än noll, se ljusets gravitella beroende om ej redan bekant börjar
neutronsönderfallet med snabbaste verkan i J-kroppens g-centrum.
Inom ett snävare avgränsat område nära
centrum ändras kurvformen för neutronkvot noll (DIAKVADRATEN) maximalt ringa vilket gynnar en idealt praktiskt taget
samtidigt ingång av en central fusionsfas:

Områdets nybildade tätt packade väteatomer
protonkärnorna börjar omedelbart utföra spontana exotermiska seriefusioner.
Figuren ovan skisserar förloppet med visst växande utrymme i det primärt
heltätt kärnpackade J-centrumet i takt med att ursprungskärnorna reduceras i
antal på mera kompakta tyngre atomkärnor:
Notera EXOTERMISKT FÖRBJUDNA
FUSIONER: alla 2H4 + 2H4¦1H1¦0n1
kan inte bilda stabila atomer på grund av att det fattas utfyllande massa (kärnelementen
stöter ifrån varandra). Vi bör känna till den detaljen i atom och
kärnfysiken i allmänhet. Tre 2He4 går dock utmärkt.
Seriefusionerna alla spontant och direkt
exotermiska utverkade i hela Järnkärnan inom max t20 sekunder
kan anta som i kärnikonillustrationen
ovan två olika sätt:
en udda form som börjar på tre 2He4 efter
bildade deuteroner 1H2 med vidare steg i 2(1H2).fusioner och
en jämn form som börjar på en enda 2He4 med
samma 2(1H2) i vidare påbyggnad uppåt;
Inga stabila tyngre atomkärnor kan bildas med den uppsättningen fusionsagenter
än max upp till Järn-Nickel.
Varfördå?
De
atomkärnor som bildas ytterligare blir av typen Jumboprotoner: atomnumret
byggs på med ytterligare 2(1H2)-föreningar så länge sådana finns, men det
fattas motsvarande utfyllande neutronmassa som matchar kärnladdningen: atomen
blir för lätt för sin byggnad och sönderfaller därför neråt till aktuellt
lättare stabila atomer.
Så slutar Järnkärnan sin uppbyggnad på en
begränsad mängd »instörtande» väte. Tomrummet som bildas mot instörtningen
garanterar f.ö. Järnkärnans egen KEMISKT isolerade tillvaro från övriga:
Järnkärnan utbildar ett motsvarande primärt utåtriktat Coulombiskt repellerande
expansionstryck mot allt ovanförvarande (närmast vätekärnor runt om).
Samtidigt under den första centrala fusionsprocessen byggs J-kroppens slutliga
kroppsrotation upp på den osedvanligt stora exotermiskt frigjorda energins
räkning. Se särskild beskrivning i PrimROT, samt energiräkningen nedan (Järnkärnan).
DIVERGENSTÄNDNING ¦ GRB-objekten ¦ TNED ¦ Ljusets Gravitella Beroende ¦
JÄRNKÄRNANS INITIERANDE
BILDNING: ironCORE
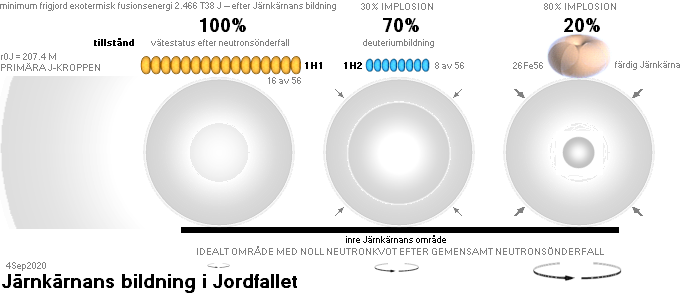
Alla himlakroppar uppvisar exakt samma
principiella centrumbildningsfysik.
Det
enda som skiljer är att lättare J-massor har svagare g-kraft och därmed större
repellerande Coulombkraft och de missar en optimal bildning av Järnkärna bara
av den anledningen frånsett vissa undantag (se exemplet Merkurius i artikeln om G-SKUGGNING).
De tyngre kropparna utvecklas istället mot typen sol/stjärna med delvis andra
förutsättningar i den centrala primära fusionsbildningen (min 6 Jupitermassor,
se Solgränsmassan).
KÄRNPUNKTEN I HÄNDELSEFÖRLOPPET med
Järnkärnans bildning är den följande:
Med implosionshändelsen »taket störtar
in» följer obönhörligt en kärnmekanisk rekylaktion:
»Centralen» strävar att »kasta tillbaka
inkräktaren» till ursprunget.
Det sker en UTKASTNING av visst (12.13% i
Jordfallet) primärt ytmaterial från den primära J-kroppsmassan.
J-BEVISET ger matematiken.
Clair: ironCORE
Sammanställningen nedan visar
uppställningen av en elementär grundmatematik med vars hjälp konturerna
klarnar:
Resultatbilden tvingar oss entydigt att
förlägga J-kroppens primära massavyttring analogt med tillfället då ironCORE den ovan beskrivna rent mekaniska stötrekylen utbildas:
från Järnkärnans initiella imploderande kärnbildning (J-beviset bekräftar/stadfäster den matematiska fysikens reella
förankring av princip) :
ENBART MAXTÄTA J-KROPPEN HAR ENERGIN
FÖR ATT AVYTTRA PRIMÄRMATERIALET
PRIMÄRA HIMLAKROPPSMASSORNA Genom direktberäkningar
Hela ämnesområdet ansluter till definitionen av FUSIONSGRÄNSMASSAN 6.80016 T24
KG med enda möjliga kandidaten som
Jordkroppens 5.975 T24 KG, och den därmed sammanhängande konsekvensmatematik
som ledde fram till HIMLAKROPPARNAS PRIMÄRMASSOR.
TRYCK-
OCH ENERGIPARAMETRAR:
D = m/V
a = Gm/R²
p = F/(A=1M²) = (m=VD)a/(M²=V/R)
= (VD)a/(V/R)
= RD · a
V = 4piR³/3
----------
p = RD · a
= Rm/V · Gm/R² = 1/V · Gm²/R
= Gm²/RV
= RD · Gm/R²
= D · Gm/R
R³ = 3V/4pi = 3m/4piD
p = D · Gm/R
= D · Gm(4piD/3m)^1/3
= G(m²4piD^4/3)^1/3
----------
E(G) = Gm²/R
E(G)/M² = Gm²/RA
= Gm²/R(4piR²)
= Gm²/4piR³
= Gm²/3V
= GmD/3
Tabell10 HONC2020.ods -- 4Sep2020 --
ENERGINOTAN till Primära Jordkroppens massavyttring -- särskilda beviset för
att endast exotermisk extra energi kan förklara helhetsbilden

Kastar man inte ut bovarna i början,
blir det svårare mot slutet: Avyttringsmassan har bästa energiförutsättningarna
för avyttring från början inte alls i slutet.
RESULTATBILD
primära massavyttringarna:

Trots en högre energinivå i J-kroppens maxtäta fysik, krävs betydligt färre
multipler (8.4) av J-kroppens tillgängliga tryckfysik jämfört med en fullt
färdigbildad himlakropp (Jorden) för att få kasta ut samma netto
materialmängd;
En fullt färdigt formutbildad Jordkropp
behöver drygt 225 000 gånger den egna tillgängliga tryckfysiska verkan för att
få ut avyttringsmassan (8.249 T23 KG) från en ursprunglig J-kroppsmassa
(6.80016 T24 KG).
Men inte heller den mera kompakta maxtäta
J-kroppen med radien drygt 200 meter kan själv mobilisera den nödvändiga
utkastande kvantiteten på tryckfysikens egen räkning ekvivalensen mellan
energimängderna som krävs för att klä utkastningsmassan i flykthastighetens
kostym.
Enda möjliga energiagenten som kan betala
hela energinotan finner vi istället tveklöst i den stora exotermiska
fusionsenergi som avges i samband med Järnkärnans bildning (J-beviset).
TERMONUKELÄRA STRÅLNINGSTRYCKET nämligen, helt frånvarande i moderna korridorer: hela
Solfysikens matematiska fysik i TNED har enorm och avgörande affektion på max
tätt liggande materia.
I
modern akademi känner man bara till ett motsvarande (ytterst svagt) kemiskt
strålningstryck, här helt och hållet utan betydelse.
COMPTONEFFEKTEN styr på vanligt sätt händelseutvecklingen: Exotermisk
fusionsenergi i form av NEUTRINOSTRÅLNING påverkar maximalt tätt liggande atomkärnor med
motsvarande påtryckande krafter. Den kraftbilden avtar i takt med mängden
växelverkande tillfällen mellan strålningskvanta och atomkärnor. Så kan (stora)
extra påskjutande krafter förstås tillkomma från just den inledande
fusionsfasen med Järnkärnans bildning som dessutom ansvarar enda möjliga
TNED-alternativet för J-kroppens slutligt utbildade egenrotation (PrimROT).
Ovanstående
räkning har tidigare inte alls ens antytts i Universums Historia. Den har
framkommit här endast i särskilt behov för att klargöra bevisa en analytisk
ståndpunkt som INTE urartar i uppenbara felslut om inget annat
revolutionerande visar sig. Räkningen stadfäster ett principiellt
detaljerat noga relaterbart beskrivningssätt.
Tidigare beskrivningar har varit enbart summerande, utan
någon direkt bevisbar kännedom om den primära massavyttringens tillfälle i
frågan hur eller när, bara faktum ATT. J-beviset ger oss den enkla uttömmande förklaringen.
Vi
får nämligen (bonus) en mera preciserad BILD av hur Jordkroppens specifika
ytfysik i atmosfär och litosfär MÅSTE ha gått till i ljuset av det ovan
redovisade resultatet tillsammans med basdata på Jordämnena.
Det blev kärnpunkten i hela händelsehistorien
med Järnkärnans bildning: Jordens Biosfär. Vattenbildning på »IsNeutroner»
garanterat bortom den här författarens möjliga penetrerande fantasi UTAN
ovanstående klara matematiska-fysikaliska hjälp (så originellt att man bara
kan häpna):
JoKYtFy: Clair
JORDKROPPENS
MINERALOGISKA BILDNINGSHISTORIA
JORDKROPPENS YTFYSIK
bildningshistoria i syntes enligt TNED-kosmologin
SCENARIO:
Se
inledningen med Kraftmorfologin vid
Kroppsbildningen, om ej redan
bekant, detaljerna återkommer här:
Med olika sfäriska regioner av nära
samhörande g-potentialer, sammanförs olika områden med specifika fusionsserier
(också via möjliga resonanser i tryckverkan under pågående expansionsfas);
Varje skalintervall kan utveckla en egen
specifik nuklidfamilj genom seriefusioner, sinsemellan skilda av »stötband» som
garanterar att bandens atomer gränsar till varandra via smala sfäriska
mellanrum som säkrar en KEMISKT icke fusionskopplade materialutveckling.
![]()
I J-kroppens toppskikt kan en sådan
materialpågående utvecklingsbild möjligen te sig som i den ikoniska
nuklidillustrationen nedan. Se efterföljande (Nov2020)mera utvecklat och
detaljerat i MATIK.
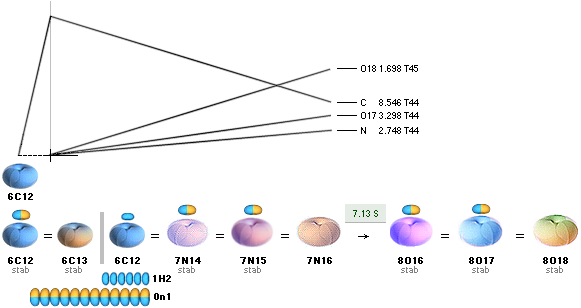
Linjefiguren från 6C12 visar en
initierande snabb kolbildning inom ett eget avgränsat fusionsband.
Kolnukliderna sins emellan är kemiskt skilda de ligger utanför varandras
nuklidbarriärer och har inte längre någon fusionskoppling. Genom att emellertid
frånsett någon sidokoppling kolnukliderna möter
kroppsytans fortfarande icke sönderfallna neutronbesättning fria neutroner
smiter lätt in i befintliga atomkärnor, det finns inga särskild spärrar .. kan tyngre
nuklider bildas enligt den illustrerade nuklidserien: 6C12 + 0n1 = 6C13 ¦ en
avvikande fusionskopplad 6C12 + 1H2 ger 7N14 ¦ och därifrån vidare upp till
tunga syreisotopen 8O18 via instabila 7N16 med halveringstiden 7.13 sekunder till
stabila 8O16. Alla dessa kan så YTFORMERAS på typ kolindivider underifrån med
ytbesättningar av icke ännu sönderfallna neutroner.
Det är också precis vad som behövs
för att förklara nuvarande Jordatmosfäriska och Jordlitosfäriska kvantiteter:
Linjerna med utritade slutnivåer
anger aktuella atomantalsmängder i atmosfär+litosfär efter kända tillgängliga
tabellvärden (Tabell6 HONC2020.ods);
Ursprungliga kolmängden avtar från
det givna primärbandet, på kredit av ALLT bildat AtmosLitos kväve och
syreistotoperna O17 och O18. Det huvudsakliga 8O16-syret bildar sedan poängen i
hela komplexet, nedan i huvudtexten.
H2OCO2: JoKYtFy
EXPANSIONSFASEN
J-kroppens normalisering från Dmax 1.82 T17 KG/M³ till färdigbildad
himlakropp med specifik medeltäthet
PRIMÄRVATTNETS SÄRSKILT GARANTERADE
CO2-MÄTTNAD
Alla stabila nuklider i Kol, Kväve och Syre kan bildas »enkelt» med början från
ett fusionskopplat kol-band;
Varje ToppKolNuklid fusionsmatar bildning
av närmast högre tyngre atomnuklid via enkla steg med befintliga neutroner i
kroppsytan som nu alltmer bör likna sin slutliga medeltäta kroppsform;
Vi
befinner oss alltså i SCENEN (långt) efter Järnkärnans bildning och en
föregående REDAN avklarad primär massutkastning typ kanske en kvart efter
eller så (Jorden är morfologiskt färdigbildad inom 20 minuter, säger TNED).
EXPANSIONSFASEN BEFINNER SIG ALLTSÅ I ETT
SKEDE AV AVSTANNANDE: kemisk bildning sker i hela Jordkroppen, och en
resulterande värmevåg är på väg upp mot kroppsytan, ännu inte markant anländ.
Dmax ¦
SCEN:
Ett STORT separat REDAN KEMISKT SÄKRAT 8O16 SYREBAND tränger upp
underifrån det ovan bildade på en nödvändigtvis förmodad allt mera långsam
slutlig kroppsexpansion:
UPPTRÄNGANDE SYRE MÄTTAR DET MINDRE KOLUTBUDET;
SYREUPPTRÄNGNINGEN PÅ DET MINDRE KOLBESTÅNDET GARANTERAR ETT KEMISKT
MÄTTAT (8O16) CO2 REDAN FRÅN FÖRSTA BÖRJAN.
KVÄVE ÄR ETT S.K. INDIFFERENT
GRUNDÄMNE. DET FÖRENAS INTE MED ANDRA GRUNDÄMNEN UTOM VID TYPEN METALLSMÄLTA:
KVÄVET SYRE-PUTTAS UPPÅT MED DET INTRÄNGANDE
SYRET NERIFRÅN CENTRUM OCH HAMNAR TILL SLUT ÖVERST;
SLUTBILDEN BLIR ETT SISTA ÖVERSTA ÄNNU ICKE
SÖNDERFALLET NEUTRONSKIKT MED EN NÄRMAST UNDER MINDRE MÄNGD KVÄVE, SAMT EN STOR
MÄNGD RENT 8O16 SOM BARA VÄNTAR PÅ NEUTRONSÖNDERFALLENS VÄTEBSÄTTNINGAR FÖR
VATTENBILDNING;
IRB: 6Sep2020 Clair
ISTÄCKETS RELATERBARA
BILDNINGSHISTORIA
UTAN Clair RÄKNINGEN OVAN HADE DEN MÖJLIGHETEN FÖRBLIVIT OUPPTÄCKT
..
Det som komplicerar hela
beskrivningsbilden är följande:
Med expansionsfasen
kemibildningen följer J-centrums normalt fasta J-kropps centrala g-trycks
överförda YTTRYCK:
den expanderande kroppssfären känner inget centrum-g-gryck. Det skjuts på
kroppsytan via expansionens g-mottryck. Särskilt vid expansionens
avstannande.
Efter det
ögonblicket sker fysiskt tvunget en slutlig kemisk normalisering: alla
differenser utjämnas med kroppsgravitationens inverkan och de inbördes
kemiskt/elektriskt/magnetiskt verkande krafterna.
TEMPERATUREN de tätt liggande nybildade atomkärnornas inbördes
repellerande krafter kan alltså INTE på »normalt sätt» förstås tillväxa i
ytan »med successivt större yt-utrymme» då sfärytan växer med expansionen. Vi
har i andra termer inget säkert begrepp om hur att få fram någon temperaturbild
VID kroppsytan UNDER [den relativt kortvariga]
expansionsfasen ANNAN än »minimal temperaturökning på grund av centralöverfört
g-tryck».
RESULTATBILDEN i kroppsytan primärt enbart sist sönderfallande
neutroner under expansionsfasen ger en bild av tätt sammanförda nybildade
atomer/atomkärnor med minimalt rörelseutrymme: Kemiska föreningar sker från
minsta möjliga atomavstånd. Det betyder i varje fall i princip »exotiska
kristallisationer» typ diamantformer eller liknande.
Kärnpunkten i resultatbilden:
J-kroppens avgörande toppsyre, dess förmåga att förenas med kvarvarande
ännu inte sönderfallna neutroner (halveringstid 12-14 minuter) renderar
följande möjliga situationsbild:
Väte flyter över 258°C¦15.15°K, förångas vid 252°C¦21.50°K.
Syre flyter över 218°C¦55.15°K, förångas vid 182°C¦91.15°K.
Förutsatt att
yttemperaturen under expansionsfasen inte märkbart ligger under syregränsen ca
90°K:
Tätt (SyreBex) tryckpackade
syreatomer förenar sig successivt med neutronsönderfallna vätepar till en
vattenmolekyl på direktform IS.
Vi har i skrivande stund inget
annat att gå på i beskrivning och uppfattning av den allmänna händelsebilden.
Använder vi allmänna gaslagens samband v²=3bT/m för att få fram ett
medelhastighetsvärde mellan fria syreatomer (ånga eller gas) vid 90°K ges
värdet v=374,5 M/S för syrets atomgas med singulära O16 och i molekylform
(O16-par) v=264.8 M/S.
DEN AVGÖRANDE SLUTPUNKTEN:
Värmevågen som utvecklas genom
hela expansionsfasen (kroppens ekvivalenta gravitationsenergi) befinner sig
under uppträngande mot kroppsytan under hela kroppsexpansionen (nuvarande Jordradie 6,378 T6 M på idealt 20 minuter
ger en medelhastighet på drygt 50 KM/h = 14 M/S);
Värmevågen når rent fysiskt inte fram till kroppsytan förrän expansionen
har avstannat, helt.
Se särskild grovillustrerad
grafisk bild av det kritiskt termiska händelseförloppet i IceTimeLINE.
OM vid det laget hela primära neutronbanken har sönderfallit till väte
och det vätet förenats med det underliggande syret till vatten i formen av IS
de nuvarande
integrerade Jordlitosfäriska 20 stycken ekvivalenta havsoceanmassorna á 1.4 T21
KG som i isform täcker ett 54 KM tjockt skal kring Jordytans nuvarande idealt
släta medelsfär, expansionens slutform
finns bara ett återstående
scenario att välja på:
När värmevågen når kroppsytan med
full pedal utbildas en hetgas
[INKOKNINGSGASENS
BETYDELSE ¦ CompilEXP] i ett smalt
område mellan Jordyta och istäckets undersida:
Hetgasen smälter omgående av ytskiktet på istakets underdel;
Vatteninnehållet börjar successivt kokas in i Jordlitosfären med
underliggande hetgasmateriel på tyngre redan färdigbildade grundämnen:
Istäckets tjocklek avtar underifrån med istakets allt högre avstånd över
Jordytan.
I slutänden finns bara ett tunnare
skikt kvar: det knäcks, faller till ytan och en sista snabbare ytavsvalningsfas
inträder: Vattnet som återstår blir vårt nuvarande 1 stycken havsoceanmassa
inkluderat att ytvatten på Jorden.
Härifrån kan den primärt helt idealt släta litosfären utveckla
topografi: toppar och dalar, och därmed begynnande landformationer.
För istäckets härledande möjliga primära fortlevnad under Solen, se
särskilt i
I takt med att neutronerna sönderfaller
till väteatomer sakta, mjukt, långsamt förenas två väte med en syre
till en vattenmolekyl. Ingen värmevåg från den samlade Coulombexpansionen har
ännu nått upp till kroppsytan kroppsexpansionen är fortfarande utpräglat
radiell men är på väg.
TJOCKLEKEN PÅ ETT SKIKT UTBRETT ÖVER HELA
NUVARANDE JORDYTAN 5.11 T14 M² PÅ PRIMÄRT TÄTT LIGGANDE NEUTRONER SOM
SÖNDERFALLER TILL HELA VÄTEATOMBESTÅNDET I 20 STYCKEN NUVARANDE HAVSOCEANMASSOR
á 1.4 T21 KG TOTALT 2.8 T22 KG ÄR OFATTBART RINGA: 37.7 pM; picoMeter: 37.7
t12 M.
Kontrollräkning:
Neutronkärnans höjd h = 1.37 t15 M; Neutronrätblockets upptagande
markpackningsyta (2h)2; Neutronkärnans upptagande volymblock
V(N)=4h3 = 1.0285 t44 M³;
Antalet Nst 1H1 i m=2.8 T22 KG vatten är 2st H per varje
vattenmolekyl med atomvikten U=2+16=18:
N/2=m/Uu =
9.368 T47; N(1H1i20HavsOceaner) = 1.8736 T48;
Totala neutronvolymen =NV(N)=1.9271 T4 M³ fördelad över Jordytan A=5.11 T14 M³
ger neutronskiktets tjocklek (t) över Jordytan lika med t
=NV(N)/A = 3.7712 t11 M = 37.7 pM.
I
takt med att neutronerna sönderfaller till väteatomer framträder följande
förklarande sinnebild:
Sakta, långsamt med varje nybildat par
väteatomer som förenas med en syreatom
SER
VI HUR ETT ISTÄCKE VÄXER FRAM »SOM UR TOMMA INTET» OCH BILDAS ÖVER JORDYTAN OCH
SOM SLUTAR PÅ TJOCKLEKEN 54 KILOMETER ÖVER SJÄLVA DEN FASTA KROPPSYTAN: 20st
havsoceanmassor á 1.4 T21 KG.
Nerifrån Jordcentrum tränger nu upp den
sammanlagda värmevågen från hela expansionsfasen (den har samma dignitet som
Jordkroppens totala g-energi):
Enligt fyra oberoende samstämmiga
FOR-källberäkningar parkerar värmevågen i Jordytan med slutbeloppet 70 000 °K
med avsvalningsfunktion mot en svalare centrum; huvuddelen av värmebildningen
sker via huvuddelen av kroppsmassan, alltså inte direkt från centrum (DFF).
Enda kemiskt stabila hetgas (ETAB) som kan
ombesörja isskalets smältning och vatteninkokning i den underliggande
litosfärens material blir en CO-O-gas, först från CO (stabil under 86 311 °K).
Det blir den mellanliggande gasdel som sammanknyter litosfär och atmosfär och
ger hela Jordskorpan dess kända syrerika och vattenrikt integrerade ytmineral
med en inkokningstid på 16.32 Gy.
GROVRÄKNAT:
1,77 T21 KGvatten/miljardÅr =
19×1,4T21/15T9;
1,77 T12 KGvatten/år (=1.8GigaTon/år)
integreras med Jordlitosfären;
Per kvadratmeter Jordyta (5,11 T14 M²):
drygt 3,5 gram/årM². Grovt vikten av ett A4-papper/årM².
Det
skulle bli (vara) hela historiens förklaring första delen. Se fortsättningen
i ISVERSIONEN (TNEDa2).
ExoEx: ironCORE ¦
FUSIONSENERGIERNA TILL JÄRNTOPPEN: Tabellen
JÄRNKÄRNANS EXOTERMISKA
ENERGI ¦ GrundämnesBildningen
IRON CORE
JÄRNKÄRNAN
TNED
DIAKVADRATEN i TNED himlakropparnas primärbildning obs visar att
Järnkärnans
storlek upptar (grovt neutronkvoten = 0 bestämmer grundvärdet) 1/3 av
Jordvolymen:
r(Järn) = rJekv/3
= 2,126 T6 M;
V(Järn) = 4πr3/3 = 4,0251158
T19 M3. Järnets täthet (tabellverk, eller egna mätdata)
är
D(Järn)
= 7 870 KG/M3. Massan i Järnsfären via D=m/V är då
m(rJärn) = VD = (4,0251158 T19 M3)(7 870
KG/M3) = 3,1677662 T23 KG. Eller i % av Jordmassan:
m(rJärn)/m(rJ) = 0,053017007 ~ 5,3%.
Diakvadraten ¦ BildningsEnergierna i Jordfallet
Järnkärnans
storlek och täthet i etablerad mening har en något mera vidlyftig
innebörd (seismiska mätningar berättar):
Kärnan måste alltså vara uppdelad i två helt olika delar, en
yttre och en inre. Man har kunnat visa att den inre kärnan måste vara fast, med
en densitet på sannolikt 13 000 kg/m³. Kärnan är i genomsnitt nästan dubbelt så
tät som manteln, så trots att den bara står för 16%
av jordens volym, innehåller den ca 32% av dess massa. Jordens
genomsnittsdensitet är 5518 kg/m³; siffran kan beräknas direkt om man känner
massan och radien.,
:
16%
av Jordvolymen (4πR3/3) ger en sfär med (54.3%) drygt halva
Jordradien:
Viron
= 4π · rIRON3 /
3 = 0.16 × 4πR3/3 ;
rIRON3 = 0.16 × R3 ;
rIRON = (0.16 × R3)1/3 = 3,4625111
T6 M = 54.2883523%R ~ 54%
TNED-värdena
för Järnkärnan betyder i jämförelse med etablerade värden i vilket fall
ett absolut sämsta fallets lägsta värdets energiräkning. Vidare nedan.
JärnKärnan: Jm-BEVISET ExoEx ironCORE Clair ¦ KroppsRotationen
5Sep2020
JÄRNKÄRNANS ALLMÄNNA BETYDELSE
IMPULSMOMENTETS SUVERÄNA SÄRSTÄLLNING I
UNIVERSUMS HISTORIA J = mvr
Järnkärnans exotermiskt avgivna
fusionsenergi (nedan: minst 2.469 T38 J) tillsammans med TNED-fysikens härledda (TNST) termonukleära strålningstryck
himlakropparnas bildning från max neutrontäthet
ingår inte i modern akademi trots avgörande för speciellt hela Solfysikens
elementära förklaring
är
den enda bevisligt här kända möjliga (Clair) energibas som existerar i TNED-kosmologin för att
förklara dels
Jordrotationens uppbyggnad
(KROPPSROTATIONEN) och uppkomst (samma princip gäller för alla himlakroppar)
och dels
himlakropparnas primära massavyttring
(JORDENS ANDRA EKVATION): förmågan att putta ut (flykthastigheten v2/2
= Gm2/r) en mindre del av primärmassan i samband med
formeringen av den aktuella himlakroppens slutligt bestämda massform
(HIMLAKROPPARNAS PRIMÄRMASSOR).
Utan den centrala energigrunden kan dessa detaljer inte förklaras varken
kvantitativt eller kvalitativt;
IMPULSMOMENTET ¦ TNST
TERMONUKLEÄRA STRÅLNINGSTRYCKET ¦ TNED ¦ KROPPSROTATIONEN ¦
JORDENS
ANDRA EKVATION ¦ HIMLAKROPPARNAS
PRIMÄRMASSOR ¦
Förklaring
J-beviset:
Bägge komplexen förklaras
kvalitativt och kvantitativt
genom
K-cellens allmänna fysik av
impulsmomentets universella bevarande
J = mvr
= konstant primärt. Se särskilt utförliga beskrivningar för hela
K-cellens matematiska fysik i Impulsmomentets KVALITATIVA och KVANTITATIVA
universella bevarande om ej redan bekant;
Utan en liten
minimalt given kroppsrotation KOMMER efterföljande fusionsfas efter
divergenständning att sönderdela hela kroppen på en motsvarande idealt statisk
explosionshändelse.
Varfördå?
Förhållandet mellan energimängderna:
Exotermiskt
frigjorda fusionsenergin enbart i järnkärnan vårt minimalt sämsta fallets
räkning 2.469 T38
J är många gånger (drygt 600 000 gånger) större än
Jordkroppens nuvarande sammanhållande gravitationsenergi 3.734
T32 J: J-kroppens söndersmulas.
1.2 T37 J
räknat på Jordkroppens Rbegin=200M [20 ggr större].
Fusionsenergins enda utväg ur centrum på den Dmax-täta J-kroppen är: radiellt.
Om istället
en liten centralt grundämnestung kärna är den som den lilla primärrotationen
får börja drivas upp på via sin exotermiskt avgivna fusionsenergi avgränsat
från den övriga J-kroppens ännu icke fullt fusionsutbildade kropp
KOMMER neutronmassan utanför den lilla
kärnan att utöva en inbromsande funktion motsvarande friktion på den snabbt
uppvarvande lilla kärnans spinn
och därmed utjämna en annars rent explosiv
effekt (typ K-cellens detonation);
Fusionsenergins enda utväg ur centrum på den Dmax-täta J-kroppen är: spiralt.
Den lilla
inre kärnans spinn avtar sedan under Jordhistorien i takt med att J-kroppens yttre
delar och kroppsyta erhåller motsvarande överförda rotation med tillhörande
värmebildningar i kroppens inre:
friktionen mellan de olika sfäriska
skikten.
Den typförklaringen blir helt utesluten i
modern akademisk kosmologi:
Föreställningen om Jordkroppens bildning
via planetesimaler
successiv
massökning genom slumpartade kollisioner och sammanstötningen med tillhörande
slumpmässigt uppkommen hel kroppsrotation
omöjliggör
den inre spinnande kärnan med dess överförda rotationsenergi på skalet.
VINTERGATAN och alla andra himlakroppar
uppvisar samma fason: en snabbspinnande central del med allt långsammare
rotationer utåt periferin.
Se även motsvarande särskild beskrivning i KROPPSROTATIONEN ¦ KRdetMag.
Resultatbild
generellt vid primärbildningen hur J kan förstås bevaras nettobilden:
Med
givet J0=mvr på en fast given primär J-kroppsradie (r¦J0/r=konstant=mv)
tvingas (CLAIR)
kroppsmassan (m) att genom mellanliggande händelser reduceras med
(i vårt Jordfall) 12.13% förutsatt (KROPPSROTATIONEN) en blott liten primärt
given kroppsrotation (v) tillväxer med samma belopp:
Primärmassornas avyttring (som i Jordfallet) fungerar bara på ett primärt
minimalt J;
primära konstanten J bevaras.
men
det är ironCORE som
ovan endast första fasen i J-kroppens rotationsuppbyggnad:
en fas som tydligen sammanhänger med
Järnkärnans initiella (ytterst snabba) bildning;
Vartefter fusionsfasen utvidgas till J-kroppens övriga delar, fortsätter de
exotermiskt avgivna fusionsenergierna på det max täta J-kroppsmaterialet att
bygga upp primärrotationen ytterligare successivt från J-centrum och utåt
kroppsytan i takt med att också expansionsfasen utbreds, och så länge
fusionsfasen varar.
Energin (grovräkningen, hela Jordkroppen
betraktat som en stel materiesfär) som krävs totalt för att ge Jordkroppen
nuvarande rotation är för övrigt ytterst blygsam i dessa sammanhang: endast
1.292453 T30 J
(ENERGIN TILL PLANETROTATIONERNA).
Jordkroppens
totalt avgivna exotermiska fusionsenergi från neutroner till färdigbildad
material- och mineralkropp är 4.6532662 T39 J (sambandet i Exempel
nedan) på nuvarande mJ=5.975 T24 KG. Jordkroppens egengravitella energi
för att jämföra [BEG: 3,734 T32 J ¦ Fd = Gm2/(rEND
rBEGIN)] är bara en försvinnande liten del.
Impulsmomentets
KVALITATIVA universella bevarande ¦ Impulsmomentets
KVANTITATIVA universella bevarande ¦
ENERGIN
TILL PLANETROTATIONERNA ¦ BEG
GRAVITATIONSENERGIN
(BEG) den ekvivalenta energi som en himlakropp spänns upp på (formeras
kemiskt mineralogiskt från ett Dmax till Dnormal) är samma som att
återföra alla kroppens grundämnen på dess primära neutroner, stänga av
elektromagnetismen helt, och sedan låta neutronerna attraheras fritt mot
g-centrum (fritt mekaniskt fall); E = Fr = Gm22/r.
Det blir densamma (kemiskt) omvända
expanderande energiform som g-energins omvändning i formen av en
CoulombRepulsion: kemiskt formerande ExpansionsEnergi från ett Dmax (R=200M
i Jordfallet) i balans med g-energin via kroppens slutform vid ett
Dnormal med R=6,378 T6 M i Jordfallet.
Det är vår enda referens i postuleringen
som ovan:
Exotermiska fusionsenergin i läge Dmax
(1,82 T17 KG/M³) maximalt tätt packade neutroner har ingen annan utväg (via
lokala ljushastigheten) än PÅ den täta neutronmassan:
fusionsenergin termonukleära strålningstrycket i idealt radiellt utstrålande mening p=F/A
utverkar ett mekaniskt tryck på all ovanförvarande kärnmassa;
är fusionsenergin större än g-energin råder
rent energitekniskt en övervikt för fusionsenergin och enbart av den
anledningen kommer INTE den överliggande neutronmassan att bevaras inom sin
J-kropp: den exploderar enbart på energiräkningens kredit.
Har
den ansvariga exotermiska fusionsgenererande energikärnan (stenkropparnas
järnkärna) däremot ett litet primärt SPINN kan
fusionsenergin dämpas och spridas ut (spiralformigt
i rotationsprocessen) tryck/friktionsmekaniskt på alla överliggande
sfäriska skal upp mot toppytan, och J-kroppen bevaras:
fusionsenergins utgång ur den svagt redan primärt roterande centralt bildade
järnkärnan
som
initieras via en deuteriumbildning en intern implosion JÄRNKÄRNANS INITIERANDE BILDNING som garanterar en central sammandragning (med
beloppet 1/√2), och därmed via det primärt givna J=mvr ett högre v via
det mindre r och därmed en initiellt garanterad rotationsseparation mellan en
mera snabbroterande kärna och en mer långsamt roterande ovanförvarande kropp
utverkar
en icke radiellt riktad påtryckande
funktion som genom den så snett riktade fusionsenergins utgång ur den
snabbare roterande centralkärnan, under dess egen pågående fusionsfas under det
centralt bevarande höga g-trycket varvar upp ovanförliggande neutronmassor
via deras mekaniskt mothållande motstånd och därigenom också reducerar
kärnspinnet
och
därmed en underhållande friktionsprocess som eliminerar/reducerar
explosionstillfället
samt reducerar centralkärnans max spinnhastighet så att dess egen kroppsyta,
centrifugalkraften, inte kastar ut sitt eget material utanför den egna
spinnande kroppsranden vid spinnmax.
BESKRIVNINGEN kan göras ännu mera
sammansatt (flera detaljer ingår, inte direkt omnämnda: separationsutrymmet
mellan den centralt imploderat initierat bildade deuteriumkärnan och
ovanförvarande garanterar en första kemisk separation ..).
EXEMPEL:
ENORMA
EXOTERMISKA FUSIONSENERGIER c = 2.9972458 T8 M/S:
GROVRÄKNINGEN sämsta fallet med lägsta
värdena DIREKT med 5,3% av Jordmassan eller 3,17 T23 KG på Järnets medeltäthet 7
870 KG/M³ via Järnnukliden 26Fe56 (91.66%) med ursprungliga A=56 neutroner (förenklat
A=U) per järnatom via N=m/Uu=3.409 T48 stycken enskilda
26Fe56:
Massdifferensen med ursprungliga antalet neutroner (U=1.0086652) × (56 × 3.409
T48) minus (56 × 3.409 T48) = 0.0086652(56 × 3.409 T48)u ger
via E = mc2 totala MINST exotermiskt
avgivna fusionsenergin i JordJärnkärnans fall värdet E = (3,17 T23
KG)(0.0086652)c2 = 2.469 T38 J.
Det är i
nettobilden bara aktuell materialmassa som räknas på neutronmantissans
atomviktsreduktion, helt oberoende av atomtyp.
Används Bonnierskällans
32% av Jordmassan står Järnkärnan i så fall för ca 1.489 T39 J i utgiven primär
fusionsexotermisk energi vid Jordbildningen.
Räkningen nedan visar hur siffrorna växer fram enbart genom de aktuella
separata fusionsstegen utan hänsyn till summeringen av föregående
nuklidprodukt.
Sammanställningen
med UDDA och JÄMNA NUKLIDGRUPPERNA i den exotermiska bildningen av Jordkroppens
Järnkärna enligt relaterad fysik (TNED) ger en uppfattning om vilka närmast
ENORMA energier som frigörs i den korta snabba fusionsfasen: primärkroppens
grundämnesbildningsfas efter divergenständning.
EXOTERMISKA BILDNINGEN AV
JORDKROPPENS CENTRALA JÄRNKÄRNA Tabell8 HONC2020.ods:
Värdena i tabellen nedan är manuellt inskrivna från
originalförfattningens exotermiskt beräknade fusionsvärden för respektive
ändnuklidgrupper neutronkvot noll som slutar på Nickel och Järn.
För att exotermiskt bilda tyngre nuklider måste
fusionsagenter introduceras med större neutronkvot än noll. Se vidare i 6C16-agenten.
Tabell8 HONC2020.ods
UDDA OCH JÄMNA NUKLIDGRUPPERNA ¦ Diakvadraten ¦ TNED ¦ JÄRNKÄRNAN I JORDEN
¦ JÄRNKÄRNAN
I MODERN AKADEMI ¦ GRB-objekten
i Universum
FÄLT i GULT anger instabila nuklider.
Deras ORANGEA makar anger den instabila nuklidens stabila slutnuklid. Vi kan följa
alla sönderfallsprocesser i detalj med tillgång till allmänna tabelldata över
experimentellt utförda analyser med början från 1900-talet och dess
omfattande experimentella kärnfysikaliska litteratur.
UDDA
OCH JÄMNA NUKLIDGRUPPERNA ger besked om hur mycket energi (värme och ljus) som
ges ut genom de primärt maximalt tätt liggande sönderfallande neutronerna i
Jordcentrum himlakropparnas primärbildning enligt TNED. Som vi ser: närmast enorma energimängder
frigörs sett enbart till den inre Järnkärnan.
UDDA och JÄMNA nuklidgrupperna ¦ Divergenständning
¦ förenklat
numeriskt exponentiellt skrivsätt i Universums Historia: T ¦ t för 10±
Tabellresultaten ovan visar att 1 KG Järn genom successiva fusioner från
bildningen av Deuterium (1H2)
sammanhänger
med en exotermisk (massförintelse) energiutgivning av kvantiteten
Eexo
~ 6,1 T14 J per KG primärt exotermiskt fusionsbildat material
(Koppar-Nickel-Cobolt-Järn-Mangan-Krom-Vanadin) med början från maximalt
kärntätt liggande primära neutronsönderfall. Eller runt 7 gram massförlust per
KG Järn (Alla runt Järn ungefär samma grovt sett).
DECIMALKOMMA OCH PUNKT ANVÄNDS HÄR KAOTISKT OMVÄXLANDE på
grund av här ofta gjorda importresultat från beräkningar i kalkylprogrammet
OpenOffice som ändrade decimalkommateringen efter import av engelskt
avstavningspaket endast vissa godtyckliga justeringar görs här.
Hela Järnkärnans bildning i Jorden:
1,9337 T38 J exotermiskt
Det
är mer än 500 000 gånger hela Jordkroppens gravitationsrelaterade
konvergens-divergensekvivalenta G-energi 3,7 T32 J. Järnkärnan enbart;
5,3% av Jordmassan eller 3,17 T23 KG; 7 870
KG/M³.
5
500 KG/M³ = 0,947·XKG/M³ + 0,053·7 870 KG/M³;
XKG/M³ = (5 500 0,053·7 870)/0,947 = 5 367,36.
För
hela Järnkärnans bildning i Jordfallet
m(rJärn)·Eexo = (3,17 T23 KG)(6,1 T14
J) =
1,9337
T38 J. Jämför hela Jordmassans E=mc2-innehåll:
(5,975
T24 KG)·(3 T8 M/S)2 =
5,3775
T41 J; Järnkärnans exotermiska bildning
bränner av runt 0,036% av hela Jordmassan för Fe-tillkomsten.
Eller
i reda kvantitet massa: m = E/c02 = (1,93
T38)/(3 T8)2 = 2,1 T21 KG för Järnkärnans tillkomst enbart.
En
hel Havsoceanmassa till jämförelse visar ca 1,4 T21 KG.
Det betyder att Jordkroppen får bada i
rejäla neutrinoduschar vid sin grundämnesbildning se visst sammanhang från
Plancks Strukturkonstant ovan[1][2] och Certifieringen av den tunga nuklidgruppen:
energiduscharna
äventyrar inte nukliderna som sådana.
Primära
bildningsprocessen av Jordkroppens centrala Järnkärna omsätter nära 2 stycken hela
nuvarande havsoceanmassors fullständiga upplösning i ljus och värme.
Energierna vid himlakropparnas
primärbildning från Dmax är i andra enklare ord med vårt enkla
räkneexempel VÄLDIGT STORA dessutom ytterst snabba (1 fusion i runda tal per t20 sekunder).
Se även i GRB-objekten i Universum.
TNED-kosmologins
basvärden primära himlakroppsbildningen
Järnkärnan i Jordens centrum upptar bara
drygt minst 5% av hela Jordmassan (32% enl. BA-citatet):
Järnkärnan utvecklar mer exotermiskt
massförintande E=mcc energi än hela Jordens nuvarande havsoceanmassa 1.4
T21 KG vid Järnkärnans primärbildning;
Primärytan (r=200M) sammanhåller
Jordkroppen med en ytaccelerationskonstant av runt 1 miljard g;
Hela den
primära Jordkroppens snabba expansion från Dmax-radien ca 200 meter till
nuvarande ekvatorialradien 6,378 T6 M innefattar
en händelse som avyttrar (flykthastigheten)
en expanderande utflyende massdel i Jordens fall på ca 12,13% av primärmassan
(6,80016 T24 KG).
GASBILDNINGEN i netto vid Jordytans
slutliga bildningsomfång bildar grunden för det Jordbiosfäriska livet.
UDDA OCH JÄMNA NUKLIDGRUPPERNA ¦ Fusionsgränsmassan 6,80016 T24 KG
¦ GRB-objekten
i Universum
hExoterm2020.ods
kalkylkorten nedan DIREKT
FRÅN DEN HÄR WEBBLÄSAREN hExoterm2020.ods se öppningsmanual om ej
redan bekant eller kopiera URL:en
nedan till valfri webbläsare (vilket som fungerar förutsatt att SVENSKA
VERSIONEN av gratisprogramvaran OPEN OFFICE finns installerad på datorn)
http://www.universumshistoria.se/AaKort/hExoterm2020.ods
hExoterm2020test.ods
kalkylkorten nedan DIREKT
FRÅN DEN HÄR WEBBLÄSAREN hExoterm2020test.ods se öppningsmanual om ej
redan bekant eller kopiera URL:en nedan
till valfri webbläsare (vilket som fungerar förutsatt att SVENSKA VERSIONEN
av gratisprogramvaran OPEN OFFICE finns installerad på datorn)
http://www.universumshistoria.se/AaKort/hExoterm2020test.ods
hExoterm2020test.ods Tabell
1  ; Tabell 2
; Tabell 2 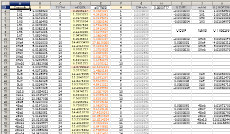 ; Tabell 3
; Tabell 3 
hExoterm2020.ods Tabell1  ; Tabell 2
; Tabell 2 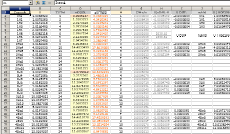 ; Tabell 3
; Tabell 3 
EXOTERMISKA KÄRNREAKTIONSLAGENS
KALKYLKORT
EXOTERMISKA KÄRNREAKTIONSLAGEN
Bilden nedan visar det numera
(Apr2020) helt automatiserade kalkylkortet för (som ger ut värme och ljus)
exotermiska fusioner,
föreningar mellan maximalt tätt liggande
atomkärnor som redan befinner sig innanför varandras nuklidbarriärer och
därigenom undergår spontana föreningar.
Kalkylkortet används för utvärdering och
resultat i uppgiften med att undersöka relevanta eller irrelevanta exotermiska fusioner mellan olika nuklidkomponenter.
Nuklidkomponenterna (agent, objekt,
produkt) är enskilda atomindivider, stabila eller instabila vilketsom; Allt vi
kan komma över i tillgängliga tabellverk som presenterar mätresultat av
uppmätta atomvikter.
EXOTERMISKA KÄRNREAKTIONSLAGENS
KALKYLKORT relaterad fysik
hExoterm2020.ods hExoterm2020test.ods
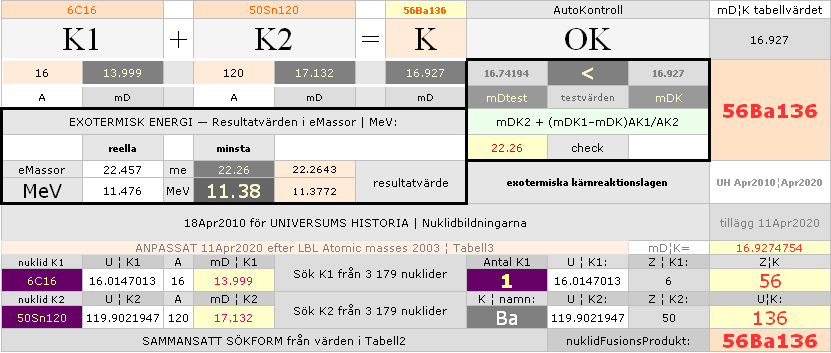
Tabellkällan
här som används
är
den omfattande LBL-tabellen (LAWRENCE BERKELEY NATIONAL LABORATORY, 2003) med
sina 3180 specificerade nuklider.
Funktion
och användning:
INMATNINGEN
görs genom att ange
ZnamnA
med betydelsen
ATOMNUMMERnamnMASSTA, typ
6C12
om inslaget inte finns (TabellA2) visas typiskt #E/T
i närliggande celler; neutronen matas in 0n1;
rutan med AntalK1 kan användas för max 2 nuklid K1.
Kalkylkortet letar upp nukliden i separat tabell (Tabekll2), tar fram aktuell
atomvikt och genomför en resultaträkning. Se särskilt (Kärnreaktionslagens
härledning) HÄRLEDNINGEN TILL EXOTERMISKA KÄRNREAKTIONSLAGEN. Den innefattar
begrepp atomära massdefekterna som inte ingår i den moderna akademins
atom- och kärnteorier.
RESULTATET
om exotermiskt visar (OK) och namnger fusionsprodukten, samt aktuellt
avgiven fusionsenergi med tillhörande parametervärden. Eller, om fusionen inte
är exotermisk (notOK):
den felande energimängden anges på raden
för resultatvärde.
alla resultatvärden här använder minsta-alternativet,
om inget annat anges.
EXOTERMISKA KÄRNREAKTIONSLAGEN ¦ Kärnreaktionslagens härledning ¦ Gravitationens Fundamentalform ¦ Nuklidbarriären
OK betyder positivt MeV-värde att fusionen är
exotermisk.
Annars
negativt MeV-värde kräver fusionen energi (den är endotermisk).
ANTAL
K1 = max2 typ fusionssteg
K1 → ¦K2¦ ← K1;
En
triplett är den enstegs fusionsordning som är fysiskt praktiskt maximalt
möjlig: TNED (atomkärnans
härledning) garanterar att mellanindividen (K2) avskärmar Coulombverkan
inbördes mellan K1-agenterna
(atomkärnan
gravitationens fundamentalform är inte transparent för elektromagnetisk
strålning: den släpper inte igenom ett endaste nå frånsett den smala öppningen
i kärnbrunnarna) mellan ändnukliderna K1 så att fusionerna verkställs från
K2-individens bägge ändsidor alla tre med samma kärnspinnriktning. Annars är
det kört.
Se utförligt från NUKLIDBARRIÄREN om ej
redan bekant.
ITERATIONSKORTET till
fusionsellipserna
Tabell 1 O34 hExoterm2020.ods

Värdena som kommer fram 1/E och K
matas in (manuellt) i grafprogrammets ellipsekvation som sedan (Enter) ritar ut
aktuell ellips för analys och illustration.
Författaren envisas med att testa
parallella system vilket kanske gör överskådligheten delvis avskräckande för
utomstående snokande (typ Microsoft&Google ..).
Bägge
kalkylkorten
hExoterm2020.ods hExoterm2020test.ods
har
använts omväxlande för att sammanställa och exemplifiera detaljerna i det här
dokumentet (TNEDa0),
fusionsellipsernas koppling till tunga
nuklidgruppen (masstalen från 60 till slut. se Amax300¦317).
Kalkylkorten
innehåller dels en (Apr2020) InternetImporterad atomviktstabell (kalkylkortens
Tabell2&3)
och
dels (delvis extensiva) resultattest på källan ovan som använts under arbetets
gång och som också behöver redovisas för den som ev. själv vill pröva vidare:
kalkylkorten är fritt tillgängliga och kan användas helt efter egna önskemål
(om man »fibblar bort sig» är det bara att ta in en ny frisk kopia).
NuklidTab4.wks2003: Utvecklingen ¦ UeDIFF Microsoft programförstörande exempel konverteringsexempel
MICROSOFT
HINDRAR kan inte KUNSKAPSUTVECKLING:
kan
inte datorer, inte matematik, inte fysik: förstår inte Konceptet. Se exempel i EOOK.
Rätta
gärna om fel (»i stort sett allt efter Bill Gates-epoken»): sakfel
får inte förekomma här:
hoppar in, gör avbrott
tar bort
försvårar utvecklingsarbetet på tidigare
perfekta arbetsverktyg genom att
förbjuda/avveckla verktyget (Microsoft
förstår inte konceptet), stänger för hela programformen: vi kan inte
utveckla ett arbete längre (Ref: EXEMPEL
PÅ MICROSOFTS PROGRAMFÖRSTÖRANDE VERKSAMHET)
framhäver eget, kräver medverkan (Microsoft
hindrar allmän Internetåtkomst 4Nov2020) agerar konsult åt Polis, Domstolar (BRÅ) och övriga samhällsinrättningar.
SÄG
DET MED EN GÅNG MICROSOFT (W10+):
»
VI HYSER FÖRAKT FÖR ALLA SOM FÖRSÖKER ANVÄNDA DATORER UTOM PÅ VÅRA VILLKOR».
4Nov2020: Google&Microsoft
förbjuder åtkomst till alla internetsidor om man inte medverkar i cookies.
Jättefint. Inte alls exemplifierad världsdiktatur per telefon. Ooneej.
1.
Var och en har rätt att äga egendom
ensam såväl som i förening med andra., A17.1;
2.
Ingen får självsvåldigt berövas sin egendom., A17.2.
Skärmdumpar med resultaten 2003 från
NuklidTab4.wks
Programmet
MsWORS 4.0 med sitt suveräna kalkylprogram bästa, enklaste, mest direkta
någonsin förbjöds att användas på dator av Microsoft efter en uppdatering
2008 i Windows Vista. Programmet
kan inte transponeras/konverteras av varken
EXCEL (Microsoft) eller OpenOffice:
dessa totalvandaliserar innehållet.
Går inte att
konvertera. Se beskrivning i EOOK.
Modern akademisk kärnteori går i
museum:
MICROSOFTS
AFFÄRSBASERADE INBLANDNING I DATORUTVECKLINGEN HINDRAR MÄNSKLIGHETENS
KUNSKAPSUTVECKLING BEVISLIGT:
Alla stabila nuklider upp till
atomnummer 27 och masstalet 59 lätta nuklidgruppens stabila nuklider i
TNED-fysiken:
kopierat här i efterhand (22Nov2020) från en Windows XP-dator:
KONKRET
KÄRNEXEMPEL SOM VISAR HUR AFFÄRSINTRESSEN FÖRSTÖR, HINDRAR OCH VANDALISERAR
KUNSKAPSUTVECKLINGENS MÖJLIGHETER
PROGRAMFORMEN SOM FÖRBJÖDS AV
MICROSOFT 2008
AVGÖRANDE
PRAKTISKA BEVIS I ATOM- OCH KÄRNFYSIKEN SOM UTRADERAR MODERN KÄRNFYSIKALISK
TEORI NUVARANDE KALKYLPROGRAM VANDALISERAR ORIGINALET I MsWORKS 4.0. ÄMNET
ANSLUTER TILL HUVUDTEXTEN HÄR I TUNGA NUKLIDGRUPPENS FUSIONSELLIPSER.
mD-SAMBANDSFORMEN SAMMANFATTAR
ATOMVIKTERNA TILL LÄTTA NUKLIDGRUPPENS STABILA NUKLIDER UPP TILL ATOMNUMMER 27,
MASSTAL 59, ENLIGT GRUNDELLIPSERNA I NEUTRONKVADRATEN
HELT OKÄND I ETABLERADE KORRIDORER MED NÄRA OMÄRKLIGT AVVIKANDE VÄRDEN
RELATIVT EXPERIMENTELLT UPPMÄTTA ATOMVIKTSVÄRDEN. Se särskilt illustrerad
jämförelse TNED/MAC och DiffGRAFERNA.
Art- och kunskapsutrotningsexperten Microsoft: [vad vi vet: »i stort sett allt allt efter Bill Gates-epoken»]:
TNED-fysiken genom NEUTRONKVADRATEN
2003: Alla stabila nuklider upp till atomnummer 27:
Varken Excel eller OpenOffice kan konvertera MsWORKS suveräna
Kalkylprogram bägge presenterar kaos. Se upphittad relaterad förklaring i EOOK.
Vi kan året 2020 bara visa skärmdumparna från originalet i Windows XP
finns inte längre året 2020.
Skärmdumpar Kopierade från MsWORKS
4.0 KALKYL NuklidTab4.wks programmet som som
Microsoft förbjöd året 2008, se



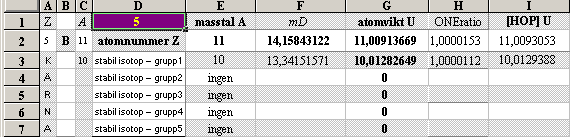


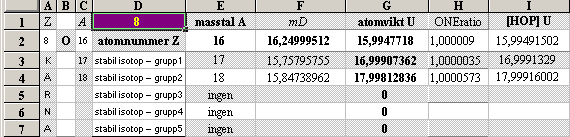
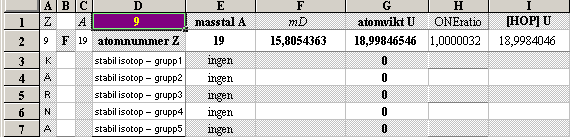
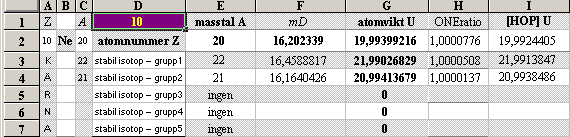
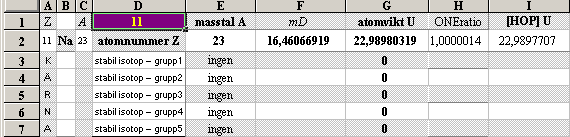
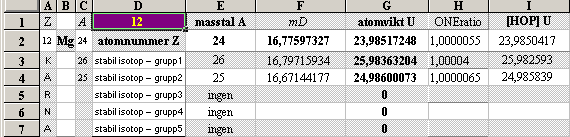

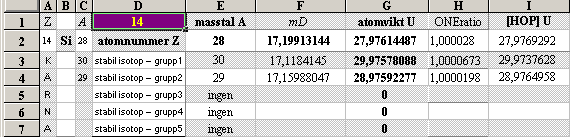
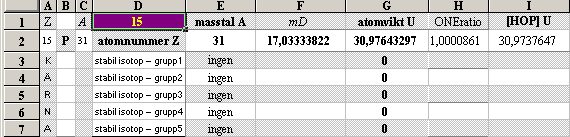
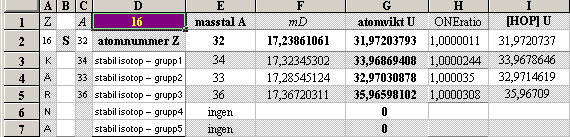
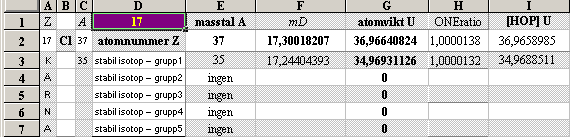
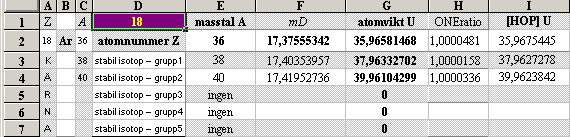

NOTERA KALIUM 40: HOP-tabellen 1967
anger den som stabil med relativ andel
0.011841%. Men Van Nostrands Encyclopedia 1976 anger den som en
betainstabil elektroninfångnings och gamma markerad nuklid β, K, γ
med halveringstid 1.3 miljarder år; HOP-källan specificerar också i kapitlet
General Principles of Nuclear Structure (s9-7sp2n) att For odd Z there are
never more than two stable isotopes. Efterkoll nu 22Nov2020 på Wikipedia
Potassium verifierar Van Nostrands-källans uppgifter: Kalium 19 har bara två
stabila isotoper, 41 och 39.
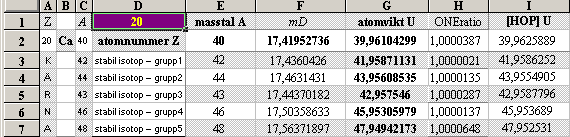

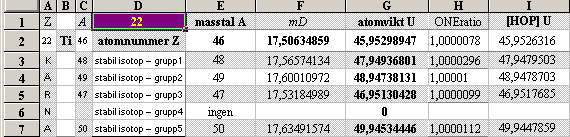
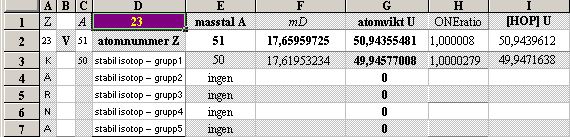
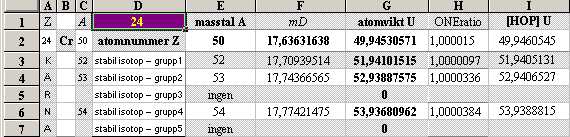

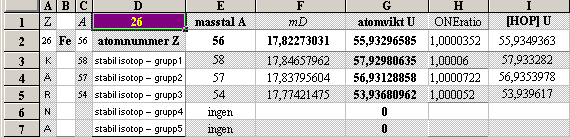

GRUPPERNA
uppvisar en systematisk ordning helt baserad och grundad på NEUTRONKVADRATEN som går att uttrycka matematiskt,
exakt numeriskt på resulterande atomvikter analoga med experimentellt
uppmätta
inom så snäva acceptabla toleransfel, att
den moderna etablerade motsvarande kärnfysikaliska teorin utklassas.
Se även i JÄMFÖRANDE
ATOMVIKTER, här mera
preciserat i DiffGRAFERNA.
ExcelOpenOfficeKalkyl: EOOK NuklidTabell4.wks 2003 KonvertEX
EXCELOpenOfficeKalkyl
MsWORKS&BorlandPascal
I samband Maj2020 med
översättningen av MsWORKS Kalkyl NuklidTab4.wks till OpenOffice-versionen:
VARFÖR KOMMUNICERAR INTE EXCEL OCH OPEN OFFICE
KALKYL MED TIDIGA MsWORKS (4.0) KALKYL (Windows 3.1, Windows95)?
Kolla kunskapsnivån: noll matematik
DelphiBorlandsPascal och
MsWORKS kommunicerar perfekt. Sedan var det slut på festen:
DELPHI(4) Borlands Pascal: x mod y
= x (x div y)
· y ¦ IF | y |>| x |
THEN x mod y = x
x div y = INTEGER(x/y)
MsWORKS och Borlands Pascal (BP) DELPHI har bägge den
MATEMATISKA funktionen för modulus (mod
fundamentalt avgörande grundbegrepp inom divisionsalgoritmen):
DELPHI(4) Borlands Pascal: x mod y =
x (x div y) · y ¦ IF | y |>| x | THEN x mod y
= x
MsWORKS Kalkyl : REST(x
; y) samma funktion som ovan
Däremot av här okänd anledning finns inte DEN typen i
Microsofts kalkylprogram EXCEL; OpenOffice har också antagit EXCEL-funktionens
sätt. Bägge använder DOCK typen Rest(x ; y) FORMELLT.
EXEMPEL:
MsW&BP
ex.: BP MsW EXC OpO
REST(2;7) 2 2 5 5
WhatsUp .. 5?
I fallen Borland/MsWORKS
är definitionen redan given från DIVISIONSALGORITMEN:
den helt enkla elementära matematiska
aritmetiska mod-funktionen med |y|>|x| ger
endast x tillbaka:
täljardelen i restbråket är redan given.
I fallen EXCEL och
OpenOFFICE sker emellertid operationen efter en annan typ,
»affärsbaserad seriesubtraktion»
eller vad det ska föreställa (Google håller på att bygga ut ..):
Den programeliten
resonerar tydligen så här:
REST(2;7) = 2/7 = (2/7
= 2 7 = 5) = (5) = 5
Antingen har programfolket bakom EXCEL¦OpenOffice helt
fullständigt missat funktionens innebörd
(förstår inte
matematiken: försöker hitta på annat, eget: vanligt i moderna korridorer 1800+,
sanningens bortgång och så där .. ingenting kan gå fortare än c .. .. men ibland behöver vi 3c för att förklara big bang .. ..)
och/eller bestämt sig för att modifiera Sättet utan att
bry sig i Konsekvenserna, om inte annat.
Vad funktionen
har för innebörd är här helt okänt.
Den ansluter i
vilket tydliga och bevisliga fall (NuklidTabell4.wks) inte till
den relaterbara kärn- och atomfysiken, som däremot BP och MsW gör: elementär detaljerad relaterbar grundmatematik;
Microsoft
(Bill Gates-eran) började tydligen helt utomordentligt rätt, riktiga
programgrepp.
Sedan urartade det .. (..
WeWantMore .. WeWantMore .. WantMoWeWant .. More .. We .. Me ..)
INGEN DIREKT
ERSÄTTNINGSFUNKTION EXISTERAR
OM programmakarna hade haft
intresse för MATEMATIKEN skulle de ha lagt in den matematiska operatorn
x mod y = x
(x div y) · y ¦ IF | y |>| x | THEN x mod y
= x
TILLSAMMANS MED »det
speciella affärshusdjuret»
REST(x ; y)
= (x y) vars användbarhet här är av typen okänd med
exempel från |y|>|x|:
Översättningen av KALKYLKOD celldata mellan MsWORKS
och EXCEL/OpO havererar i vilket fall i allmänt kaos:
Ingen direkt ersättningsfunktion
existerar.
Det går inte att ens försöka konvertera
utan att hamna i en ren överraskande orkan som sliter sönder allt.
ATOM OCH KÄRNFYSIKEN
ÄR TYDLIGEN INTE DE MEST FRAMTRÄDANDE ÄLSKLINGSÄMNENA FÖR OPEN OFFICE OCH »NYA
TIDENS MICROSOFT».
Finns inte den grunden,
finns inget alls i någon egentlig värdemässig seriös mening.
Några exempel i försöken att
konvertera NuklidTabell4.wks till
EXCEL/OpO:
Mars2020
inledningen till TUNGA NUKLIDGRUPPENS FUSIONSELLIPSER: vi skulle försöka
presentera en helhet ..
med Microsofts nuvarande attityd och
intelligensnivå är det tydligen en ren fundamental omöjlighet fasten
seatbelts, no smoking:
0. Minst kaos uppkommer om MsW-originalet
först kopieras till Excel, sedan därifrån till likartade OpO;
Flera olika
överföringsalternativ finns att välja på. Man får pröva sig fram ..
1. MsW → OpO resulterar i att OpO
blandar ihop MsW-konstanterna (176 stycken):
2. Utan vetskap om det, i en första
observation av några enstaka blir slutbilden:
OpO puttar
runt konstanterna vartefter de justeras, så att tre timmars arbetet med att
försöka städa upp resulterade i Tillbaka På Ruta Ett.
3. En del är särskilt förtjusta i intensiva
jobb.
4. Man måste alltså skriva om varje varenda
cell i sitt korrekta originalnamn, först .. eller?
5. Alla OpO-konstanter måste raderas: OpO
sätter in egna som inte fungerar.
6. Men: en manuell inskrivning i varje cell
ersätter inte (heller) cellnamnen i cellsambanden.
Man måste
alltså skriva om hela cellmatristabellkomplexet igen och ersätta, manuellt,
alla nyligen inskrivna cellnamn KolumnRad med motsvarande nyligen återinsatta
konstanter.
Det är
NORMALT SETT FÖR VANLIGA DÖDLIGA: ETT OMÖJLIG MANUELLT ARBETE SOM INNEBÄR STORA
UTRYMMEN FÖR FÖRSMÄDLIGA ÖVERFÖRINGSFEL:
7. Vi kommer inte fram på den vägen.
8. OpenOffice. Fyrhjulsdrivet med TRE.
9. TEST MED OLIKA KLISTRA IN ALTERNATIV VISAR
SAMMA MODIFRÄS (testat på Alfa-konstanten)
OpenOffice
kopplar INTE konstantcellernas angivna plats.
Och då kan vi
lika gärna skippa alltet.
Det blir FEL,
fEl, FeL överallt.
10. RADERAS FORMLER i OpO sedan EXCEL-kopian av
NucTab4.wks kopierats till OpO
RADERAS INTE
SAMTIDIGT KONSTANTERNA: dessa kvarstår.
11. Något Alternativ RADERA KONSTANTER verkar
inte finnas. (Wao).
Fyrhjuling
bara med backväxel. Fantastiska datorprogrammeringskunskaper. Alla böcker
slutsålda.
12. FÖR ATT RADERA KONSTANTERNA MÅSTE MAN GÖRA
SÅ HÄR i OpO manuellt, varenda post:
1. Ctrl + F3
konstantfönstret kommer upp:
2. Klicka på
Konstanten i Konstantlistan.
3. Klicka på
Radera.
4. En
DialogRuta kommer upp "är Du säker på att Du .." MÅSTE KLICKA OK.
(Det är tur att
Industrin INTE har satt dessa programgenier på uppgiften att producera kullager
..).
5. Börja om
igen med nästa från 2. ovan 176 stycken.
Alt+R; ENTER;
Vänsterklick (med Peken på översta) 176 gånger. OpenOffice.
MAN KAN BARA
MARKERA EN I TAGET.
13. OPENOFFICE ÄR INTE KONSTRUERAT AV PERSONER
SOM FÖRSTÅR DATORER:
värdet av
datorn som arbetsverktyg verkar inte ha någon verklig, rent fysisk
representation.
14. FÖRSÖKER MAN KOPIERA IN EN ENSTAKA
CELLFORMEL I ETT I ÖVRIGT FORMEL OCH KONSTATNTTOMT OPENOFFICE, EXCELKOPIAN
RENSAD PÅ ALLT CELLINNEHÅLL UTOM SJÄLVA DESIGNUPPLÄGGET MED TEXT OCH FÄRG, SVARAR
OPENOFFICE MED ATT KOPIERA IN HELA RUBBET MED DE FELAKTIGA KONSTANTERNA IGEN
SOM VI NYSS HADE TAGIT BORT:
Jag hade inte
givit löfte om något sådant.
Hur kopierar man då in
originalcellkoden utan att påtvingas open office-intrånget med konstanterna, som
OpO inte heller kan hantera?
Genom att
försöka en kopia ta bort alla konstanter från excelkopian, och testa från
den.
EXCEL har en
enklare raderingsprocedur ingen mellandialog kommer upp.
Bara Alt+T; SPACE för varje. Inget Enter.
VAD HÄNDE?
Ersatte EXCEL
konstantnamnen i cellsambanden med Cellvärdena KolumnRad?
Inte.
Konstantnamnen står kvar, medan konstanterna raderats:
EXCEL tar bort LIVET ur Kalkylkortet OM man
raderar konstanter=Särskilda Cellnamn.
Som vi ser: hur man än försöker, är
det EMOT. Inte MED. Praktiskt taget omöjligt att få fram originalet: stabila
nukliderna upp till masstal 60 via exakt definierad matematik i MsW och BP.
Summa summarum
Enda sättet
är att SKRIVA OM HELA CELLKOMPLEXET med äventyren inbegripna i exemplet ovan,
samt en del ytterligare Excel och OpO kommunicerar på samma typkoder, vi
exemplifierar här med Excel:
MsWORKS:
INDEX(beteckning;0;Z0)
EXCEL:
INDEX(beteckning;Z0+1;0+1)
MsWORKS:
VLETAUPP(Z0;nuctab;15)
EXCEL:
LETARAD(Z0;nuctab;15+1;FALSKT)
ex.: BP MsW EXC OpO
REST(2;7) 2 2 5 5
Vi får kämpa
med
HELTAL
AVRUNDA
FÖRKORTA och
REST
som betyder att
läsaren av det här inte alls vill veta något mer av plågan det innebär att ENS
försöka:
Stabila
nuklidernas matematikkomplex kräver MATEMATIKEN divisionsalgoritmen exakt.
Och den finns tydligen varken i EXCEL eller i OpenOffice.
SLUTBILD:
Försöken här
hittills har lett fram till följande med vissa inre oönskade bieffekter:
En OpenOffice kopia (NukTab4.ods) har
utformats som klarar att VISA alla nuklider som i MsW-originalet inte
relaterat i cellkoderna, dessa är rena kaoset som ovan, enbart i resultatrutan
utom för atomnummer 3 och 5: (det tog flera intensiva dagar att
åstadkomma)
cellfelen är (ännu) så korrumperade att
ingen lösning har visat sig.
Korrekt masstal ska vara 6 och 7. EXCEL OCH OPEN
OFFICE KLARAR INTE GRUNDFYSIKEN. MsW&BP gör det galant.
Korrekt masstal ska vara 10 och 11. EXCEL OCH OPEN
OFFICE KLARAR INTE GRUNDFYSIKEN. MsW&BP gör det galant.
Den intressanta
frågan skulle möjligen bli:
finns en
sådan lösning alls på någon begripligt läsbar svenska?
REST-exemplet säger det rent ut: no mother god
loving way.
Det handlar
inte om ett ENSTAKA överföringsfel, utan om en KOMBINATION av sådana, typ
sedan man justerat på ett ställe,
dyker det upp fel på två nya ..
Om framställningen inte är relaterad, om
den inte kan begripliggöras i varje detalj, är kunskapsaspekten förlorad.
KonvertEX: NukTab4
GODTYCKLIGA EXEMPEL FRÅN
författarens arkiv ANTECKNINGAR
EXCELerror.txt i samband med försöken att överföra NuklidTab4.wks till
EXCEL/OpenOffice Apr2020:
konverteringsexempel NuklidTab4.wks MsWORKS 4.0
till EXCEL 11Apr2020+
MICROSOFT KAN INTE HANTERA KUNSKAPSGRUNDERNA i
exempel inrättningens allt mer tydligt affärsbaserade dikterade världsmonopol
och kapade datorvillkor har intvingat mänskligheten i ett ytligt tillstånd av
nollkunskaper säg att påståendeformen är fel, galen, det vore önskvärt men
saknar bevisgrund, rätta gärna om fel:
(man tror inte ATT det är sant);
EXCEL D100:
=macU1*macU1*(1-macU1*macU1)
Originalet från MsWORKS 4.0 Kalkyl stabila nukliderna i lätta
nuklidgruppen upp till atomnummer 27 och masstal 59 utklassar modern kärnteori:
=A*mn*(1-H95*me)
:
EXCEL E90:
=tabREF
Originalet från MsWORKS 4.0 Kalkyl:
=tabU0
:
EXCEL E81:
=OM(tabU0>0;INDEX(tabU0;tabU0+1+tabU0-tabU0+1;4);"")
Originalet från MsWORKS 4.0 Kalkyl:
=OM(C2>0;INDEX(nuctab;3;zFoundAtRow+1+A-förstzA);"")
VORE DET INTE ENKLARE ATT STOPPA IN KODERNA I lottoburken, SNURRA,
OCH KAST UT KOMPONENTERNA slumpvis? Jättefint. Alla vinner idag. Hurra!
E89:-0,098044578
=(0,1*SIN(0,2*ROT(thetaCOSINUS*(120+thetaCOSINUS))))*thetaCOSINUS
MsWORKS:
=(0,1*SIN(0,2*ROT(A*(120+A))))*Theta15
Hittar den programpersonalen ens till HemmaParkeringen? Jättefint.
Julafton 24/7.
E79:17,50634859
=(mD0-(-1)^mD0*mD0*0,2*ROT(mD0*(120-mD0*(mD0-mD0)^((1-mD0)*2^(mD0)))))+mD0
MsWORKS:
=(Alfa0-(-1)^Theta2*Beta0*0,2*ROT(Sigma0*(bPAR0-AKE^((1-Theta15)*2^(Lda)))))+thetaCOSINUS
:
E8:1
=AVKORTA(1-(ABS(Theta2/2-1)-(Theta2/2-1))/2)
MsWORKS:
=HELTAL(1-(ABS(Z0/2-1) - (Z0/2-1))/2)
Vem står ut med att i efterhand ens tänka tanken att försöka städa upp
efter Microsoft+?
Inrättningens programmerande SLARV uppmärksammades redan omkring
Windows95-eran (Explorer bombade flera program som fick sina DLL-filer
korrumperade: stavningskontroller försvann, m.m.):
Städar inte ut FÖRE återinstallation från CD lämnar gamla korrumperade
filer kvar som omöjliggör korrekt nyinstallation;
Man får ta bort föregående installerat manuellt, själv. Då gick det.
Jämför Microsofts rekommenderande support: Be personalen om hjälp datorn
köptes på att återinstallera ... Elp. Sedan dessa har mitt förtroende för
Microsoft reducerats till minus 1: personalen talar vänligt och hyggligt, men
kan inte datorer: kopplar inte logiken bakom.
E9:1
=(56+3*AVKORTA(1/E2))/56
MsWORKS:
=(56+3*HELTAL(1/A))/56
:
K106:1232
=LETARAD(K102;$S4:$AG1362;15)
MsWORKS:
=VLETAUPP(K102;$S4:$AG1362;14)
***EXCELKORREKTION:
=LETARAD(K102;$S4:$AG1362;14+1;FALSKT)
Man står ut bara så länge man står ut.
:
M78:17,50634859
=mD-(-1)^mD*mD*0,2*ROT(mD*(120-mD*(mD-1/mD*(mD-mD)/30)^(mD*2^(mD))))+mD
MsWORKS:
=Alfa-(-1)^Theta2*Beta*0,2*ROT(Sigma*(120-Sigma*(bPAR0-1/E*(AL-K)/30)^(E11*2^(Lda))))+gammaCOSINUS
:
Med många, många, många flera.
:
DET FINNS SÄTT ATT BYGGA STABILA OCH ROBUSTA OPERATIVA DATORSYSTEM,
UTFORMADE FÖR MÄNSKLIGHETEN ATT KUNNA ANVÄNDA FÖR AVANCERAD MAXIMAL SUPERSNABB
KUNSKAPSUTVECKLING: fritt, gratis, som allmänt kunskaps och
undervisningsmaterial. ABSOLUT. VI HAR SETT EXEMPLEN I NÄRBILD. MEN INTE MED
MICROSOFT AFFÄRER ENTERPRISE SOM STYRANDE RESURS. INTE ENS MED EN CHANS PÅ
KOSMOS SAMLADE ANTAL ATOMER. NO WAY. Den inrättningen blev körd i samma stund
man satte affärsintresset över datorn.
Se även det remarkabla RESTEXEMPLET.
STATSAUKTORITETENS PROMINENTA
PAROLLER 2010+: för ökad säkerhet och trygghet AM3
A3. Var och en har rätt till liv, frihet och personlig säkerhet. JÄMFÖR
SÄKERHETENS BEGREPP I SVERIGE 2020
en
dikterad övervakning inlåsning: påtvingad
växande naturavgränsning datorstyrd sinnesmanipulering i växande
2010+ (STATSFRÖJDEN) som visar och bevisar
enbart ytterligare tillfälle för
inrättningar som anser sig besitta nycklarna till himmelriket »ViVetBra» att
utöva auktoritärt bestämmande och bemyndigande fortsatt lydnad och
bestraffning i än mer synbart växande
i takt med växande brist på omdöme och
ansvar
Vad kul att du engagerar dig .. HBvinj2020
som staten inte lyfter fingret för att
motverka eftersom det skulle innebära reducerat auktoritärt bestämmande:
.. varje individ och varje organ i
samhället .., (K1¦K8¦A29.1)
MED BEVISNINGEN:
K1 UDHR10Dec1948:
EFTERSOM
igenkännandet [eng. recognition] av den inneboende värdigheten
och av de lika och omistliga rättigheterna för alla medlemmar i mänsklighetens
familj är grundvalen för frihet, rättvisa och fred i världen
ÄR
ALLT ANNAT EN DEFINITION PÅ UTÖVANDE FÖRTRYCK: icke-frihet, icke-rättvisa,
icke-fred. Satanism. Nazism. Fascism. Diktatur. Klassisk historia.
SVERIGE
ett auktoritärt naturmördande naturföraktande skräckvälde på Jorden 2020.
Säg
det: du har fel: DU HAR FEL. Säg
det. Visa. Berätta. Exemplifiera. Sakfel får inte förekomma här.
Staten
2020 gör allt annat än vad den borde göra för att främja,
underhålla
och bedriva kampanjer 24/7 för det enda botet som finns:
grundvalen
för frihet, rättvisa och fred i världen
.. varje individ och varje
organ i samhället .., (K1¦K8¦A29.1)
TNED
FRÅN BÖRJAN 1980+
innehåll: SÖK på denna
sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla
webbsidor
Universums Historia
CHEOPS REKTANGEL ¦ TNED FRÅN BÖRJAN FUSIONSELLIPSERNAS
fullständiga FÖRKLARING I TUNGA NUKLIDGRUPPEN Apr2020
innehåll
NKref NEUTRONKVADRATEN
Syntes Vad går hela den här
framställningen ut på?
MacTNED Modern akademi kontra relaterad
fysik
Elaw ENERGY LAW
EnLagMassBeg Energilagen och massbegreppet
FEfullTNED FUSIONSELLIPSERNAS FULLSTÄNDIGA
FÖRKLARING I TNED INLEDANDE EXEMPEL
InSaTex INLEDANDE SAMMANSATT EXEMPEL SOM
VISAR och bevisar ÄMNETS CERTIFIERADE ÄKTHET
Elaw1 MASSA (m) SAKNAR UPPHOV
föreställningen om ett världsallt med ändlig begränsad massa DÄRFÖR ATT
ENERGIN GÖR DET
NKbasic NEUTRONKVADRATENS HÄRLEDNING
INNEFATTAR ELLIPTISKA EKVATIONER
GN Grundnukliderna i
TNED-Neutronkvadraten 1H1 1H2 1H3 2He3 2He4
ElementsBegin
GRUNDÄMNESBILDNINGEN GENOM FUSIONSPROCESSERNA I DE PRIMÄRA HIMLAKROPPARNA
DiffGraferna MODERN AKADEMI OCH RELATERAD
FYSIK
U1U2 KAN OLIKA mD-VÄRDEN=ATOMVIKTER
FÖR EN OCH SAMMA ZnamnA FINNAS? Naa ..
FEalla FUSIONSELLIPSERNA I LÄTTA OCH
TUNGA NUKLIDGRUPPERNA TILLSAMMANS
FElt Fusionsexempel, Lätta-Tunga:
FusEPSprinc FUSIONSELLIPSERNA AV PRINCIP
GbilDetSid HUR GRUNDÄMNESATOMERNA BYGGS UPP
MED BÖRJAN FRÅN NEUTRONERNA I RELATERAD FYSIK
NKcert NEUTRONKVADRATENS ÄKTHETSBEVIS
AMax300 NUKLIDKARTANS GRÄNS Amax=300
FexVert Funktionsexempel, vertikala
tvärellipserna
BelPrecEx BELYSANDE PRECISIONSEXEMPEL
PEX PRECISIONSEXEMPEL Järntoppen i
Neutronkvadraten
Eps6C16 FUSIONSAGENTEN 6C16 MED
EXOTERMISK FÖRDJUPNING IN TILL TUNGA NUKLIDGRUPPEN
JmfGN Jämförande Grundnuklider
NFM NEUTRONKVADRATENS
FUSIONSELLIPTISKA MORFOLOGI
EUAKIFE EXPERIMENTELLT UPPMÄTTA ATOMVIKTER
KOPPLAR INTE FUSIONSELLIPSERNA EXAKT
mD8O18 ATOMÄRA MASSDEFEKTSVÄRDET FÖR 8O18
enligt Neutronkvadratens anvisningar
TripelDet TRIPELBESTÄMNINGAR unika
mD-värden i Neutronkvadraten
TRIPA TRIPELITERATIONERNA
FEhur FUSIONSELLIPSERNA hur?
ITkort NUKLIDEXOTERMISKA ELLIPTISKA
ITERATIONER
FirstTry FörstaFörsöket
Ku6C16 KURVSKARAN 6C16
ISH INRÄTTNINGAR SOM HINDRAR OCH FÖRSTÖR FÖR
KUNSKAPSUTVECKLINGEN
NinoSoP NEUTRINOSPEKTRUM OCH
PRIMÄRFUSIONERNA, enligt TNED
PSKref I TNED ÄR PLANCKS KONSTANT EN
STRUKTURKONSTANT
ComptonIll Comptoneffekten illustrerad
NucRadRef Kärnradierna
GBref GRUNDÄMNESBILDNINGEN
JrnKrnIll JÄRNKÄRNANS INITIERANDE BILDNING
Clair ENBART MAXTÄTA J-KROPPEN HAR ENERGIN
FÖR ATT AVYTTRA PRIMÄRMATERIALET
JoKYtFy JORDKROPPENS YTFYSIK
H2OCO2 PRIMÄRVATTNETS SÄRSKILT GARANTERADE
CO2-MÄTTNAD
IRB ISTÄCKETS RELATERBARA BILDNINGSHISTORIA
ExoEx FUSIONSENERGIERNA TILL JÄRNTOPPEN
FusionIRONtop JÄRNKÄRNANS EXOTERMISKA ENERGI
JrnKrnan JÄRNKÄRNANS ALLMÄNNA BETYDELSE
Jbeviset
IMPULSMOMENTETS SUVERÄNA SÄRSTÄLLNING I UNIVERSUMS HISTORIA J = mvr
ExoJorFe EXOTERMISKA BILDNINGEN AV
JORDKROPPENS CENTRALA JÄRNKÄRNA
KALKYLKORT EXOTERMISKA KÄRNREAKTIONSLAGENS
KALKYLKORT
NTwks2003 Skärmdumpar med resultaten 2003
från NuklidTab4.wks
EOOK EXCELOpenOfficeKalkyl
MsWORKS&BorlandPascal
SPP2020 Säkerhet och Trygghet
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen
i HOP allmän referens i denna presentation, Table 2.1 s965986.
mn =
1,0086652u ...................... neutronmassan
i atomära massenheter (u) [HOP Table 2.1 s965]
me =
0,000548598u .................. elektronmassan
i atomära massenheter (u) [HOP Table 10.3
s7155 för me , Table 1.4 s727 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s727,
1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG
............... atomära massenheten
[FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära
massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W
(2005)]
u = 1,6605402 t27 KG .......... atomära
massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27
KG ...... atomära massenheten [från www.sizes.com],
CODATA
rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe
on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten
i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på
1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7155]
Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.
[FM]. FOCUS MATERIEN 1975 Fysikens, kemins och astronomins historia. Allt från atomen till universum fysik, kemi jordvetenskap och astronomi. Register med appendix.
FOCUS
UPPSLAGSBÖCKER · STOCKHOLM
[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)
T ¦ t för för 10^ + ¦ ; förenklade exponentbeteckningar gör
matematiken mera överskådlig
MAC, här ofta använd
förkortning för Modern ACademy etablerad
vetenskap sedan början av 1800-talet
TNED Related PHYSICS And MATHEMATICS
Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.
(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska
Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som
följer av härledningarna i Planckringen
h=mnc0rn, analogt Atomkärnans
Härledning. Beskrivningen enligt TNED är relaterad,
vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt
logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås
(således) också
RELATERAD FYSIK OCH MATEMATIK.
Se även uppkomsten av termen TNED
i Atomkärnans
Härledning.
SHORT ENGLISH TNED in general is not found @INTERNET except under
this domain
(Universe[s]History, introduced @INTERNET 2008VII3).
TNED or Toroid Nuclear Electromechanical Dynamics is
the dynamically equivalent resulting description following the deductions in THE PLANCK
RING, analogous AtomNucleus Deduction. The
description according to TNED is related, meaning: all, each, details
claim to be fully logically explainable and understandable, or not at all. With
TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the
emergence of the term TNED
in AtomNucleus Deduction.
Senast uppdaterade version: 2023-12-11
*END.
Stavningskontrollerat 2023-12-11.
rester
*
åter till portalsidan · portalsidan är www.UniversumsHistoria.se
∫
α ω √ → ∞ τ π ħ ε UNICODE often used charcters in mathematical-technical-scientifical
descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡ ↔↕ ħ ℓ
Ω
Φ Ψ Σ Π Ξ Λ Θ Δ
α
β γ δ ε λ θ κ π ρ τ φ
σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈
≥ ← ↑ → ∞ ↓
ζ
ξ
Arrow symbols, direct via
Alt+NumPadKeyboard: Alt+24 ↑; 25
↓; 26 →; 27 ←; 22 ▬
23
↨ also 18 ↕; 29 ↔
Alt+NumPad 0-25, 26-...
☺☻♥♦♣♠◘○◙♂♀♪♫☼►◄↕‼¶§▬↨↑↓
→←∟↔▲▼
!#$%&()*+,-./♦812...
åter till portalsidan · portalsidan är www.UniversumsHistoria.se