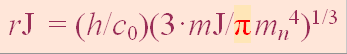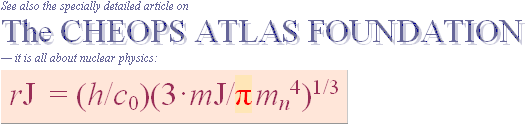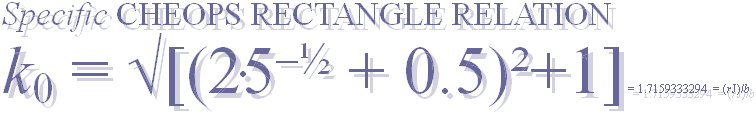CHEOPS ATLAS ¦
UNIVERSUMS HISTORIA | a![]() production 2020I1 | Senast
uppdaterade version: 2024-03-01 · Universums Historia
production 2020I1 | Senast
uppdaterade version: 2024-03-01 · Universums Historia
innehåll
content denna sida · webbSÖK äMNESORD på
denna sida Ctrl+F · sök ämnesord överallt i SAKREGISTER · förteckning alla webbsidor
NatCH
¦ PetrieQuotes
¦ HowSTART ¦ ENTER ¦ MainConstruct ¦ PetrieDAngles ¦ CheopsATLAS-Pyramids ¦ CheopsATLAS-TNED ¦ CheopsAT ¦ Resolution 217 ¦ C14darting
|
Cheops
Atlas Begin THOUSANDS
OF YEARS BACK FROM HERE some established sources claim, in some parts, a
no-easy- explainable
glaciation history — only over the northern Earth part. THAT promotes a
further GeoATLANTIS investigation.
See a special treatise glaciation article in this CheopsATLAS series modern rebellious parvenu. |
— Calling ATLANTIS .. ello ..
ello .. 222 ..
333 .. ¦ ATLANTIS ¦ GTursprunget2019 ¦ AtlantisAPPENDIX ¦
— Roger .. Roger .. Mayday .. Mayday .. A GEOATLANTIS
might EXPLAIN some GLACIATION VARIATIONS — GeoATLANTIS NORTHERN HEMISPHERE
GLACIATION VARIATIONS
• Background.
— The naming or THE TERM CHEOPS
RECTANGLE is my own early label: Tracking the original math connection bd=h2
back to The Cheops Pyramid was clarified during a shorter library literature
research (See sw. HistoryBackground [around the
time when Intel presented its first microprocessor 8080]).
The term CHEOPS
RECTANGLE was adopted by this author after a late
20th century detective search — in libraries: The most early known mentioning
of the unique and very geometrical-developing useful connection bd=h². It was
rhetorically used by Galileo Galilei, Apollonios and Pythagoras, further
backwards mentioned as an Egyptian ancient form connected to the Cheops
Pyramid.
— We respect that tradition here,
and adopt the term to it.
 ————————————————————————————————————————————
————————————————————————————————————————————
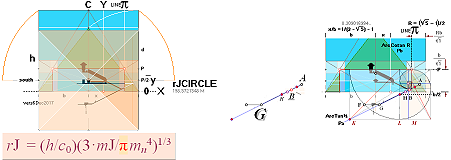
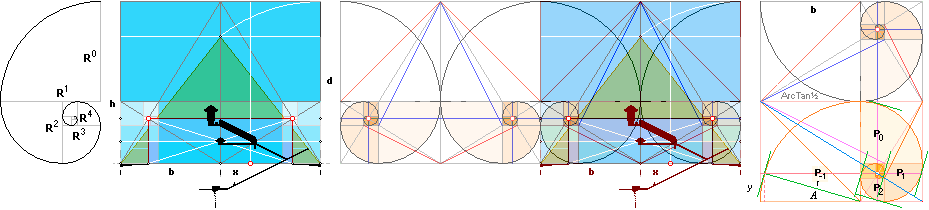
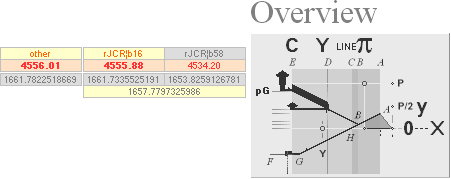
k0 ¦ GOLDEN SECTION BODY — R ¦ 18 ¦ rJ ¦ rJCR¦b16
ENTER — MiUNIT. These and others provably breach
modern archaeological ideas of the origins: exact quantitative proofs. A
correspondingly exposed building plan appears: as so extracted — from
the rJCIRCLE
complex:
GOLDEN SECTION CHEOPS RECTANGLE MATH.
We study the
details: THE TWO PYRAMID CONSTRUCTIVE
AGENTS.
CONTRACTED CONSTRUCT: Main OVERVIEW — The
Cheops Pyramid proof of a Contracted Construct ¦
![]() RECURRING CONSTANTS @3 SITES — The cSIDE
RECURRING CONSTANTS @3 SITES — The cSIDE
The GOLDEN SECTION Cheops Rectangle Complex ON the actual physical Petrie 1833 measured CheopsPyramid
|
No
uninitiated will
understand |
||||||
As we
know:
— There
are no real or DIRECT measures of the Golden Section (CHEOPS RECTANGLE) details
INSIDE the Petrie 1883 measured The Great Cheops Pyramid (conv. Khufu
Pyramid, after late modern Egyptology consensus). As injured as the building
is in our days, there is neither such a measure outside it.
—
THROUGH the Golden Section Paragon Arithmetics and Geometry, however, all Petrie measuring points and their
coordinates relative the Petrie discovered Pyramid’s ½ square base (PetrieCP¦b=4534,40’’
± 0.25) can — has shown to
— be calculated with excellent precision. That we will expose in this
presentation — on the shoulders of all those who have made contributions to the
Petrie established Cheops Pyramid metrics, their tolerances and presentations.
To be noted: Several later 20th centuries
sources have verified and asserted Flinders Petrie’s measuring work on Cheops
Pyramid as genuine. See CHEOPS
SOURCES with some excerpts to
underline the community.
EQUALITIES:
Compiled 25Jan2020 — CRATLAS0 — detailed sections ¦ CRATLAS1 — OVERVIEW ¦ CRATLAS2 — The B¦D¦PG
POINTS detailed ¦ MultipleR
DETAILED
EQUIVALENTS
EQUALITIES
rJCIRCLE-COMPLEX CALCULATED EXACT QUANTITIES WITHIN THE PETRIE GIVEN MEASURED
TOLERANCES
Cheops Pyramid versus Cheops Rectangle from the Golden
Section paragon geometrical mathematics based onThe rJCIRCLE
THE
INNER DESIGN OF THE PETRIE MEASURED CHEOPS PYRAMID IN rJ EQUIVALENTS
Beginning
(BackGround)
from the so called Queen’s Chamber:
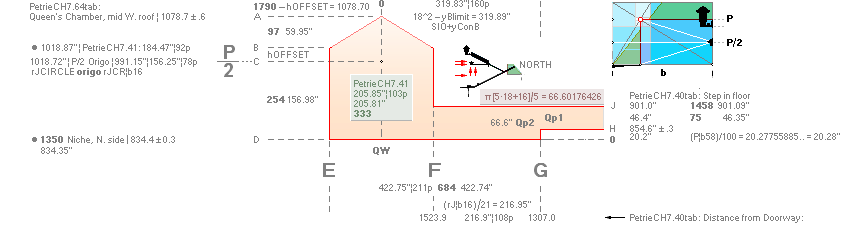
QUEEN’s CHAMBER
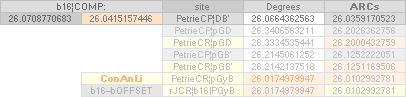
See also part of the below in IntroEX — R = [√5 — 1]/2 ¦ b1 = rJCR¦b16 = 4555.88’’:
rJCalc: A = 1790R — hOFFSET ¦
B = A — 97R ¦ C = b1/2√5 ¦ D = 1350R ¦ BD = 254R
+ hOFFSET ¦ AD = R[97+254] + hOFFSET ¦ EF = 333R ¦ FG
= ¦ b1/21 ¦ J = 1350R +
π·[5·18 + 16]/5 ¦ H = J — 75R ¦
— »The Egyptian working crew must
have been psychic». MustBuyBook.

— ’Scuse me: Several Tight Nominal fits around 0.005
inches is definitely no coincidence.
QUEEN’s CHAMBER:
PetrieNOM.B:
........... (PetrieCH7.40tab¦D=834.4) +
(PetrieCH7.41¦BD=184.47);
PetrieNOM.AD:
........ (PetrieNOM.B=1018.87) – (PetrieCH7.40tab¦D=834.4);
AS SEEN: ALL APPROVED EQUALITIES
Lead/Suggestion:
AS CONSTRUCTORS aiming at a SIMPLE, not too hard, to deduce plan for the whole
construct, we would restrict our choices to a narrow set of CONNECTING
CONSTANTS, thereby certifying/strengthening any deductive approach. Such
restricted constants or numbers in this complex are
5—GoldenSection ¦ 18—CheopsRectangleNuclearConnector ¦ 16—PyramidAgentNumber ¦ π ¦ R ¦ type R(n+182)
—
These appear recurrently in the construct quantities as exemplified in the
links. See also MultipleR
examples.
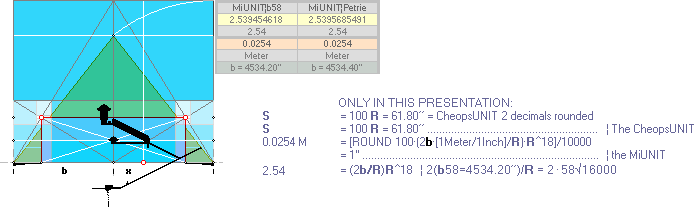
In EXPLICIT for the numbers 18¦58: see MiUNIT: 1’’ = 0.0254 M = R^18·PyramidSquareBase/100R 2decRound;
2 × (PetrieCR¦b58=4534.20 OR
PetrieCP¦4534.40) · R^17 = (2.53945.. OR 2.53956.. ) ~ 2.54.
—
Both apply.
KING’s CHAMBER
THE
INNER DESIGN OF THE PETRIE MEASURED CHEOPS PYRAMID IN rJ EQUIVALENTS
COMPARING EQUIVALENT PETRIE FIGURES
WITH The CALCULATED rJCIRCLE COMPLEX QUANTITIES

The OK cell code: IF Difference >Tolerance THEN print
”notOK” else print ”OK”. OK means: approved. NoProblemo.
In general
(Quote),
Petrie certifies that the Gallery roof top is quite unexplored due to its
inconvenient and narrow allowing inspecting space (hazardous height [8.6 M] for
any normal pedestrian without specialized security arrangements).
THE
GALLERY ROOF TOP SLABS
—
Petrie gives though some vital clues to a first rough understanding of the
construct at site, illustration below right:
KING’s CHAMBER+: EqualitiesKING
Special Links: S=MiUNIT ¦ PetriePG ¦ First Observation ¦ KingWidth ¦
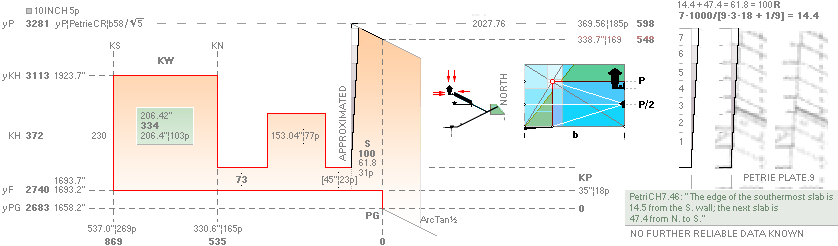
AS SEEN: ALL APPROVED EQUALITIES
Petrie
mentions in PETRIE618 the
Great Step value ”61.8±.8¦9” 5 times. We are
—
hence, even with a much smaller tolerance (± 0.1) and rounded with 2
decimals
—
clearly allowed to adopt a safe and convenient Golden Section
100R = 61.80’’ Petrie Measuring APPEARING CHEOPS
RECTANGLE MiUNIT,
for further test.
THE GALLERY ROOF TOP:
—
Petrie’s figures
”14.5
from the S. wall; the next slab is 47.4 from N. to S”
(PetrieCH7.46
In Quote specifies no roof top
tolerances, and no further details are known here on that site)
give
a possibly tight fit (± 0.1’’) with two MiUNIT coherent candidates:
• 14.4 modified from Petrie’s 14.5, summed up
with 47.4 gives exactly 61.8 = 100R.
— The
Petrie mentioned 7 LAPS from Gallery roof top down to the Pyramid S. wall then
evenly counts as
14.4 = 7 · 1000/(3 · 9 · 18 + 1/9) = 7000/(486 +
1/9) ¦ 14.4 + 47.4 = 61.80;
• 14.5 with modified 47.3 gives the same
Cheops MiUNIT 61.8 with an even 7 resolution
14.5 = 58/4 = 7 · (2 + 1/14) ¦ 14.5 + 47.3 = 61.80;
The PetriePLATE.9 drawing in comparison (above right: magnified from the @Internet
Source original) shows a fair
resemblance. But no further related data on this part is known here.
See further on THE GALLERY
POINT ¦ THE
GALLERY TOP.
CheopsATLASintro: MP1: Compiled 19Feb2020 ¦ PART 2 ¦ PART0
CHEOPS
PYRAMID CONSTRUCTION PLAN DETAILS SETTLED by rJCIRCLE Complex — Jan2020
FULLY PETRIE CERTIFIED CALCULATED QUANTITIES
Constructive OVERVIEW WITH LINKS — by order of deduction — PART
I ¦ all Pyramid measures in Inches: 1INCH = 0.0254 M.
AT FIRST TO BE OBSERVED WITH 100% CLARITY UNLESS ALREADY
FAMILIAR: The NUMBER 18. We are dealing with a
connection of which modern academy scholars have no idea: TNED deducing — not inventing — nuclear physics through
natural constants — The rJCIRCLE connection:
— The Neutron Square — atomic masses = experimentally
measured [HOP]
— is completely unknown to modern academy. And it will never be adopted either:
modern academy ideas of nuclear physics IS a primitive — Provable in every
atomic detail, or not at all. Faulty statements are not allowed here. This writ
focuses 100% on that statement.
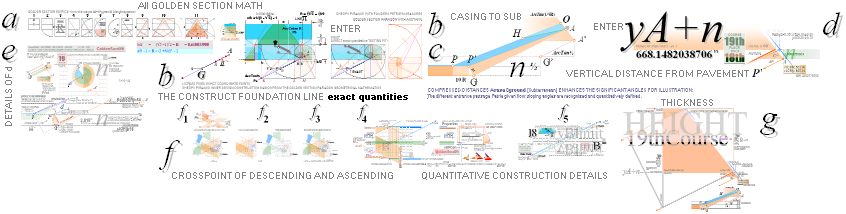
ab:
With all the general data known of The Great Pyramid
CHEOPS PYRAMID from Flinders Petrie 1883, we see a beginning from the
absolute most simple (a: The GS-body):
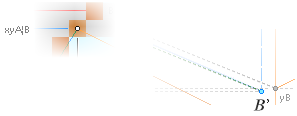
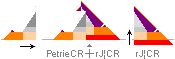
— The Most (a) obvious GS-body visual FIT generates (b) a foundational ArcTan½ construction line of 7
fundamental KLMGHBA xy COORDINATE points. 6 of them certifies the
genuineness of the 7th casing ENTER point (A) by intersection
math calculus by check and cross check reckoning. This is the foundational
construct line.
— From the notified Cheops Pyramid
rJCIRCLE FIT, we use the two pyramid Golden Section agents (b1) rJCR¦b16 and (b2)
PetrieCR¦b58 as exact numerical agency quantitative generators to test their values
against the Petrie measured: they should DEFINE the Petrie working group
results — within the Petrie given tolerances, or not at all.
c:
— Establishing (c) the basic foundational GS-body xy
points between ENTER at the casing (A) and subterranean END (G), a first Petrie (P) xy-point definition is found. P
is situated (exactly) between the vertical difference (yG–yG’) of given
by the two pyramid agents within Petrie’s given tolerances:
— PetrieCH7.36e
states: ........ x4228±2?; y1181±1?.
— rJcalc: ................................. x4227.9960057324; y1181.2240228242.
— The ½(yG–yG’) nominal (2.8172301665) difference
(The nValue) has an ArcTan½ triangle
hypo-side (n√1.25=3.1497590802)
close to π=3.1415926.. Taking the suggestion, we adopt the piFORM as a
piVersion for n (and report occasionally throughout our results the
(discernible) difference between the two (asserting that any of them will do
..).
de:
— Namely (d): Simply Summing yA + nValue directly defines the Petrie
measured 19thCourse Stone Masonry Floor Level above the Petrie pavement:
— PetrieCH7.35 states
: ........ y668.2±0.1.
— rJcalc: ................................. y668.1482038706. (ROUNDED
668.15→668.2). Nominal Difference: 0.052’’.
The details (e)
(ENTER) expose the connections.
fg:
The GS-body paragon gives us (f) direct interpreting instructions in how to connect the descending
and ascending tunnel parts through their common referring coordinate point (B):
— At first the Petrie measured B-point is rJCIRCLE
complex
defined:
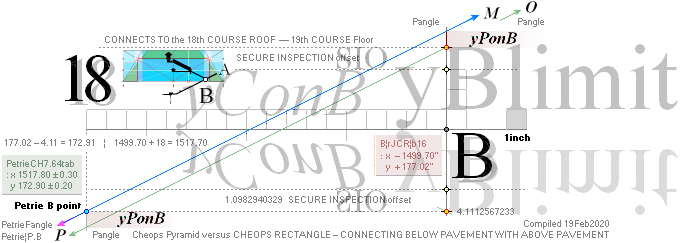
— PetrieCH7.39¦64tab
states: x1517.8±0.3; y172.9±0.2.
— rJcalc: ................................. x1517.7016293661; y172.9045085255.
NomDiff: x0.098; y0.0045.
The (f)
delicate Two pyramid agent Mutual Function Principle (TOMFIP)
— actual physical pyramid and the ideal Cheops Rectangle rJCIRCLE
b16 agent —
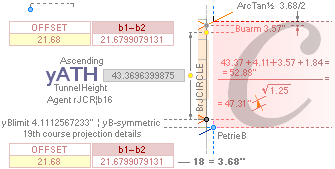
includes an internal bOFFSET value (21.68’’=21.6799079131). It — obviously —
functions as a »Construction Sealing Certificate» pushing the rJ-calculated
construction values into the final PetrieCR¦b58 agent — featuring the real physical
PetrieCP measured edifice, as here described. So to speak:
— No Cheops Pyramid Tourists are allowed to Understand
The Construct unless so »enlightened in the basics».
— Most definitely no 1800+ modern academic scholars. Guaranteed excluded.
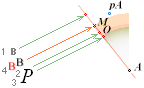
The B-point (f)
complex gives (g) all the summing constants and parts leading directly
to the GS-body Cheops Rectangle rJCIRCLE complex definition of the
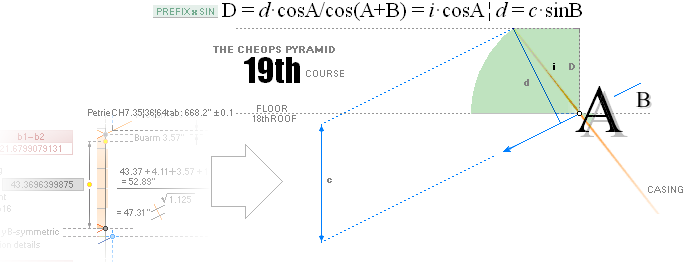
height — thickness — of the PetrieCH6.32 unveiled and so decisive 19th course masonry
»pyramidic principle» (PROVING THE PETRIE 19TH FLOOR
ARITHMETICS):
— PetrieCH6.32 states: .......... 37.94±0.17.
— PetrieValuesCalc: ............... 37.9640590055.
— rJcalc: ................................. 37.9657350065. DecDiff: 0.0017.
These coherences prove the affinity details between the
actual physical building and the Golden Section paragon
CHEOPS RECTANGLE structural plan.
CheopsATLASintro: MP2: Compiled 19Feb2020 ¦ PART1 ¦ PART0
CHEOPS
PYRAMID CONSTRUCTION PLAN DETAILS SETTLED by rJCIRCLE Complex
FULLY PETRIE CERTIFIED CALCULATED QUANTITIES
Constructive OVERVIEW WITH LINKS — by order of deduction — PART
II ¦ all Pyramid measures in Inches: 1 INCH = 0.0254 M.
WITH The full corresponding Petrie measured Cheops
Pyramid Golden Section CHEOPS RECTANGLE B-point
determination from the two pyramid agents rJCR¦b16 and
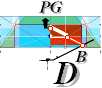
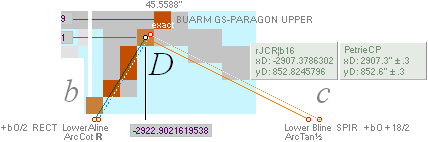
PetrieCR¦b58, the crucial sloping top Gallery floor PG point is defined
and identified with Petrie’s given values:
— From PetrieCH7.46: .......... 1658.2±0.6.
— rJcalc: ................................. 1658.1652607385. NomDiff: 0.035.
The D
point (TP26detailed) between PG and B — the floor level
into the Petrie named Queen’s Chamber at the Gallery’s lower north beginning —
is rJCIRCLE
complex
identified with the Petrie (averaged mean) specified values in offsetting the
regular direct GS-body FIT as depicted (TP26detailed) in the illustration above:
— From PetrieCH7.39: .......... x2907.3±.6; y852.6±.3.
— rJcalc: ................................. x2907.3786302; y852.8245796.
NomDiff: 0.079; 0.225.
on the SIMPLE intersection offset (horizontally
contracted) operation
bOFFSET/2 ¦ bOFFSET + 18/2 .......... see full details in TP26.
— See also complementary ways below in Petrie on Queen’s Chamber.
The rJCIRCLE complex Cheops Pyramid inner design Golden Section CHEOPS RECTANGLE construction plan
is exclusively proved in this clear cut obvious
quantitative precise Petrie precision TRANSPOSED connection:
TransPond:
— yKINGgallery THE TRANSPOSITIONS
This
is also some real steel: parameters connecting begin and end of the
ascending tunnel:
20Feb2020. Discovered transposition
equivalent: RECURRING QUANTITIES exposes A Construction plan: B point to
Gallery PG point.
——————————————————————————————————
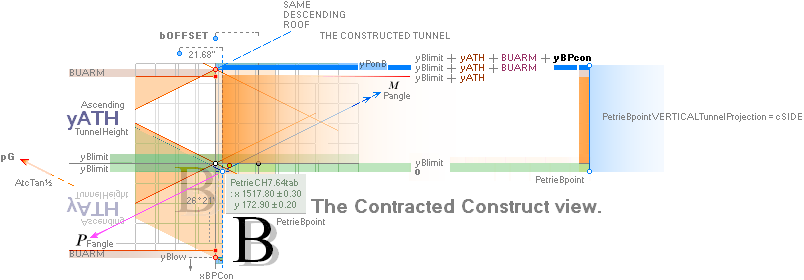
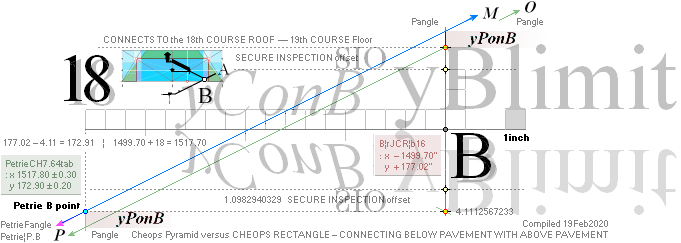
yATH ¦ BUARM ¦ yBlimit ¦ yPonB ¦ Fangle ¦ yBarm
Same rJCIRCLE complex CONSTRUCTION PLAN parameters
reused.
The rJCIRCLE complex calculated B-point parameters
transposed onto the top sloping Gallery floor, obviously defines the Petrie
given figures with some high measure of tightness:
King’s Chamber PetrieCH7.46, floor level:
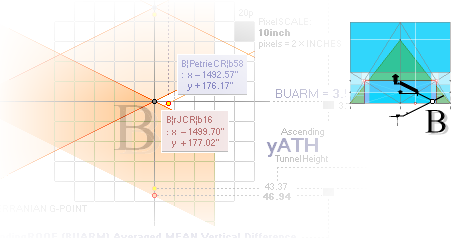
yKINGPetriePG: ....... 1693.2 ± 0.6:
yKINGrJcalc: ............. 1693.1782168993.
NomDiff: 0.022 as follows:
+ yPG ......................... = 1658.1652607385
+ yBlimit ..................... = 4.1112567233
+ S/2
........................... = 50R = 30.90169944 = 1693.1782168993.
The yBlimit+50R is mentioned by PetrieCH7.46
(”34.92 or 35.0 on E”) as the Step Face height: = 35.0129561608.
Further examinations on whole number
R-multiples also give other alternatives in approving on Petrie correspondences
within his given tolerances.
— See more examples on King’s and
Queen’s Chambers in Multiple R Values.
KING’s MIDDLE:
King Chambers Mid-point from pyramid vertical midpoint:
KCM¦PetrieMean: ................ 433.8±0.8.
rJcalc with multiple already defined and
used parameters:
KCM¦rJ: ................................ 433.6963998752 = 10yATH;
KCM¦rJ: ................................ 433.5981582616 = 20bOFFSET;
yATH/bOFFSET = 2.0004531459.
— Both rJ¦KCM lie within Petrie’s given tolerance.
We have no here
known arguments to exclude these as intended from an advanced construction
plan.
The two chambers widths and lengths also approve from rJcalc
on multiple R:s within the Petrie given
tolerances as follows;
The final collapse is approaching — the condition of the
building around 1883, King’s Chamber
”.. especially as it must be remembered that this shows its actual state, and not precisely its
original form.
On every side the joints of the stones have separated,
and the whole chamber is shaken larger.
..
These openings or cracks are but the milder signs of the
great injury that the whole chamber has sustained, probably by an earthquake,
when every roof beam was broken across near
the South side; and since which the whole of the granite ceiling
(weighing some 400 tons), is upheld solely by sticking and thrusting.
Not only has this wreck overtaken the chamber itself, but
in every one of the spaces above it are the
massive roof-beams either cracked
across or torn out of the wall, more or less, at the South side; and the
great Eastern and Western walls of limestone, between, and independent of
which, the whole of these construction chambers are built, have sunk bodily.
All these motions are yet but small—only a matter of an inch or two—but enough to
wreck the theoretical strength and stability of these chambers, and to make
their downfall a mere question of time
and earthquakes.”, PetrieCH7.51e.
:
” The position of the King’s Chamber in the Pyramid is
defined thus: N. wall at base
330.6 ± .8 S. of centre of pyramid; S. wall
537.0 ± .8 from centre; E. wall [corrected error]
=
305.1 ± 3.0 E. of centre; W wall
107.7 ± 3.0 W of centre. .. ”, PetrieCH7.55.
• (537.0 + 330.6)/2 = 433.8 ± 0.8 ................... chamber midway distance from centre;
• 537.0 – 330.6 = 206.4 ± (0.4) ....................... SouthNorth chamber width
• 305.1 + 107.7 = 412.8 ± (3) ......................... EastWest chamber length
— But PetrieCH7.51 also states
” For example, the N. wall is on average 412.59 inches long”.
PetrieCH7.52Tab gives a TopMeanBase-table with
NS-values ranging 411.88→412.78 (diff.: 0.90) and
EW-values ranging 205.97→206.43 (diff.: 0.46).
— With Petrie’s chamber conditions in quote, the original (very) precise measure is obviously
disrupted ”only a matter of an inch or two”,
making every precise comparison (here) out of the question; Speculations (here)
are not allowed. Especially not in terms of stated tolerances in the range of 3
inches.
— A rJ examination of the ± 0.4 tolerance
206.4 inch value for comparison shows:
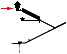
KING WIDTH South→North
KW¦PetrieCH7.51Mean: .................... 206.4±(0.4).
KW¦rJ:
................................................ 206.4233522425. Diff: 0.023;
KW¦rJ = R(10+182) = 206.4233522425.
The corresponding King’s Chamber EastWest length is, as quoted, clearly corrupted by its huge stated tolerance
(±3.0’’). In his CH7.52 table, Petrie gives us (at best) a South wall value of
412.11 inches for rJ comparison:
KING LENGTH West→East
KL¦PetrieCH7.51¦52: .......................... 412.11 (earth quake corrupted as quoted, uncertain value).
KL¦rJ:
................................................ 412.1996887244. Diff: 0.090;
KL¦rJ = (PetrieCR¦b58 = 4534.1965759686)/11 =
412.1996887244.
— No doubt there is some Basic Construct Plan going on
here ..
We test for the same route on the Queen’s Chamber:
” In the Queen’s Chamber it seems, from the foregoing
statement that the ridge of the roof is exactly in the mid-place of the
pyramid, equidistant from N. and S. sides; it only varies from this plane by a
less amount than the probable error of the determination.
The size of the chamber (after
allowing suitably for the incrustation of salt) is on an average
205.85 wide and
226.47 long,
184.47 high on N. and S. walls, and
245.1 high to the top of the roof ridge on E. and W.
walls. ..”, PetrieCH7.41.
In a following table Petrie gives tolerance values
ranging –0.17→+0.29 for the South-North width (we adopt a rough worst
case ±0.10), and –0.50→+0.56
for the East-West length (we adopt ±0.50 but will use only ±0.30):
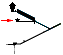
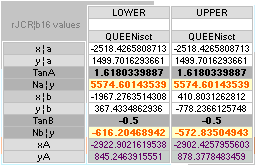
QUEEN WIDTH South→North
QW¦PetrieCH7.41: .......................... 205.85(±0.10).
QW¦rJ:
................................................ 205.8053182537. Diff: 0.045;
QW¦rJ = R(9+182) = 205.8053182537.
QUEEN LENGTH West→East
QW¦PetrieCH7.41: .......................... 226.47(±0.50).
QW¦rJ:
................................................ 226.7098287984. Diff: 0.24;
QW¦rJ = (PetrieCR¦b58 = 4534.1965759686)/20 =
226.7098287984.
In both pairing cases
KING WIDTH South→North
KING LENGTH West→East
and
QUEEN WIDTH South→North
QUEEN LENGTH West→East
the rJCIRCLE complex apparently uses exactly the same
calculating method:
(PetrieCR¦b58 = 4534.1965759686)/11or20
to gain the results.
— That obviously associates a very strong connection to A
PRINCIPAL PRINCIPLE EXISTENCE OF a foundational plan: precise advanced
constructiveness. We don’t know (yet) from where, only that it is standing
there.
— No doubt: The search for an answer IS a very exciting
expedition: — »Will we ever find it? How did it go? Was it shiny?».
Another Queen site value in a simple Number18 coherence:
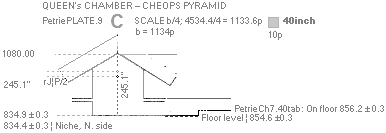
With further Petrie Queen Chamber values (the site is
partly rough and uneven), the roof top (245.1’’) from the floor level
(834.9’’) measures precisely
1080’’: 834.9 + 245.1 = 1080;
— That is also exactly the product of 60 and 18:
60 · 18 = 1080.
QUEEN SPECIAL
Specifically for the QUEEN FLOOR LEVEL yQUEEN
contra the KING FLOOR LEVEL yKING, and the rJCIRCLE
complex
transition parts already used (even closer that the yQUEEN multi R-alternative):
THE QUEEN CHAMBER LEVEL ABOVE THE PETRIE PAVEMENT
Compare the direct GS-body alternative in The Petrie D-Point.
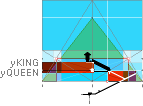
PetrieCH7.40tab: ”856.2 ±.3 ¦On floor”;
Petrie yQUEEN: .................... 856.2 ±.3
rJcalc:
.................................... 856.2949417436.
NomDiff: 0.095;
yQUEEN = yKING/2 + bOFFSET – 18 + 2yConB = 856.2949417436 ~ 856.3:
(1693.1782168993)/2 + 21.6799079131 – 18 +
2(3.0129626904) = 856.2949417436.
The bOFFSET – 18 part in explicit (it also
connects to the yPonB part) is the horizontally contracted
result of which vertical (ADD1.84) ArcTan½ spouse marks the casing spotting
limit (The Petrie available visual space between 1 and 4) from the
actual physical floor descending passage construction:
The details — the
FIT in the edifice — are somewhat and sometimes so amazingly astonishing that
one sometimes wonder if these quantities and numbers with their figures,
really, are real or just a magic dream. Those who made it really had a feeling
for it.
the physical possibility along the descending entrance
passage of finding the actual Petrie measured casing spot (pA)
connecting The 19th course floor level. See details from ENTER unless already acquainted.
What is known
here:
— The above exemplified coherences makes it impossible to
reject »The Plan» as ”a mere coincidence”.
— It — the rJCIRCLE Golden Section Paragon CHEOPS
RECTANGLE geometry — is obviously an integrated detailed description of the
whole edifice as The Great Cheops Pyramid.
The Great Cheops Pyramid
WHY THE HOLLOW CONSTRUCTIONS — ”air shafts”, ”ramp
holes”?
— The inner core masonry has, apart from the tunnel
systems some additional ”air shaft channels” and specifically in the Great
Gallery sloping floor ramp along its side, some peculiar rectangular hollow
vertical details of unknown function.
— What’sUp?
PetrieCH7.41 (Queen’s Chamber) mentions measurement
influence from
”incrustation of salts” and CH7.43 ”salt exudation”.
These are obviously long time effects (thousands of years
depending on climate conditions).
Apart from a possible sophisticated »ventilation system»
(reducing chemical attacks on the tunnel walls during long periods of time),
the ramp issue may have some alternative explanation. See THE OTHER HOLES.
Advanced
engineering.
CheopsATLASmain:
MP0: Compiled Jan2020 — PART1 ¦ PART2
CHEOPS
PYRAMID CONSTRUCTION PLAN DETAILS by rJCIRCLE Complex
FULLY PETRIE CERTIFIED CALCULATED QUANTITIES
Constructive OVERVIEW QUANTITIES WITH LINKS — by order of
deduction — PART III
Not
much in this presentations seems to be known in modern quarters.
— The
Golden Section Paragon Body
forms the unique bd=h2 triangle or
pyramid section here coined CHEOPS RECTANGLE:
GOLDEN SECTION EDIFICE — how the unique
bd=h² pyramid triangle appears:
Through
TNED observations from the rJCIRCLE
which envelopes the GS paragon
Cheops Rectangle body, a seemingly very precise layout structure coherently
appears from the 1883 Flinders Petrie group measured CHEOPS PYRAMID:
MODERN ACADEMY IS CHALLENGED by the simple GS-paragon body fits on The Cheops Pyramid edificial design:
Investigating
the apparent CHEOPS PYRAMID¦rJCIRCLE¦GS-body
coherency, simple and straight quantitative matches show up — from a basic The 7 Points xy coordinate set through the GS paragon’s ArcTan½! Line. We will see and study how the general whole of the
Cheops Pyramid construct is explained in detail on lengths and angles from this
coherent fit — in perfect match with Petrie’s given values and their specified
tolerances. The compilation below has links to the more detailed actual
describing sections, unless already familiar.
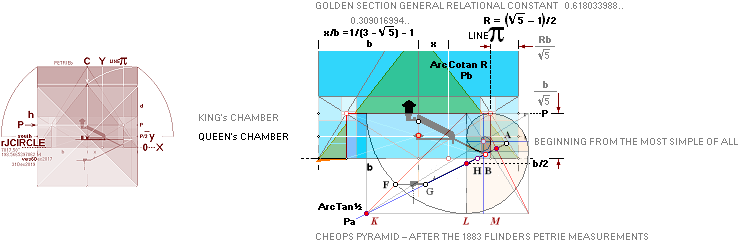
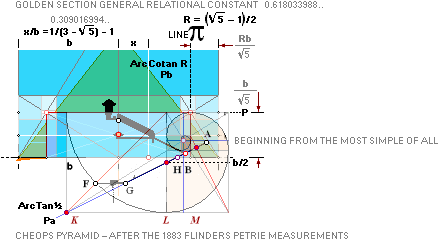
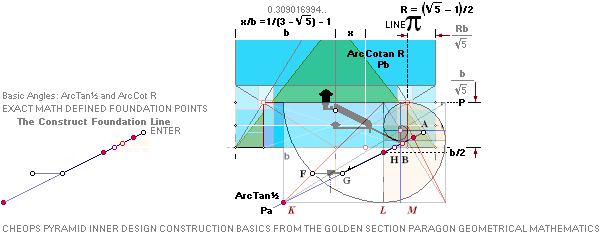
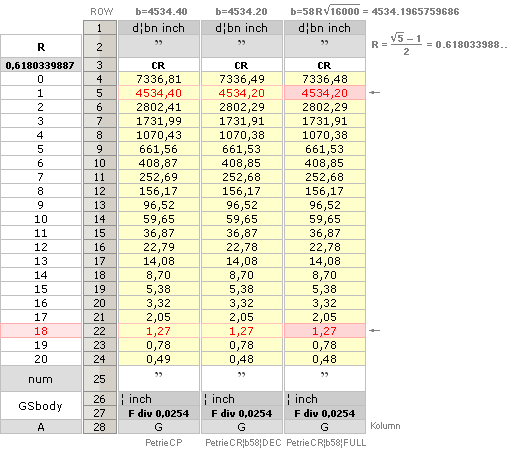
R = (5^½
— 1)/2 Point A: FULLY PETRIE CERTIFIED CALCULATED
QUANTITIES
unitINCHES rJCR internally calculated formula/term
——————————— ————
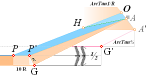
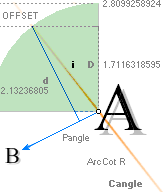
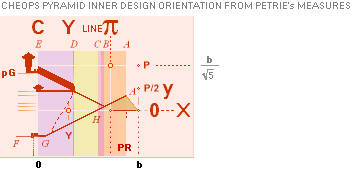
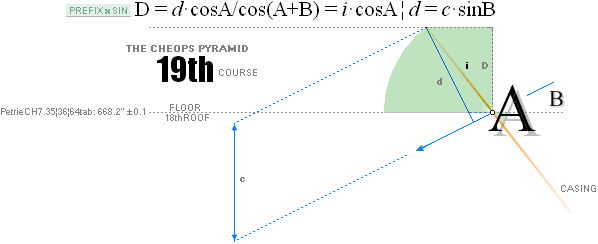
Tunnels 26° 33’ 54.18’’ A° = ArcTan½
CASING Angle 51° 49’ 38.25’’ C° = ArcCot R^½
nValue 2.817¦2.8172301665’’ (yG — yG’)/2 = (1184.04 — 1178.41)/2
= 5.63/2 = 2.815’’
FULL DECIMALS: 1184.0412529906
— 1178.4067926577 = 2.8172301665’’
yA 665.34¦665.3382779782 GS 7
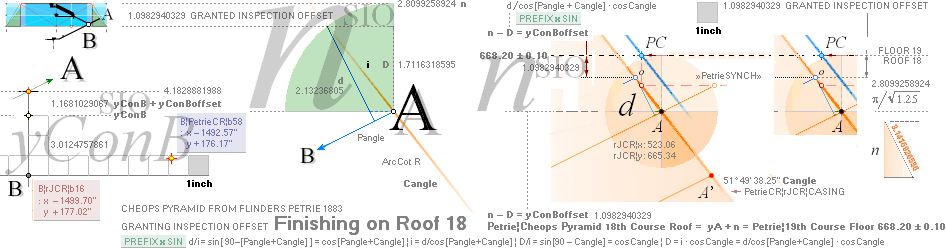
19thFLOOR y 668.15¦668.1482038706 yA+n
xA 523.06¦523.0566039073 GS 7
unitINCHES PETRIE MEASURED/calculated rJCR calculated Petrie formula/term
——————————————— ——————————— ————
CASING Angle PetrieCH6.24¦32 51° 53’ 20’’ ±
1’ not
(fully) connected PETRIE°* ROOF18 ¦ Petrie’s19th ¦ ENTER
19thFLOOR y 668.20 ± 0.10 668.15¦668.1482038706 yA+nValue
yA 668.20 ± 0.10¦PetrieCH7.36 668.15¦668.1482038706 yA+nValue
xA 524.10 ± 0.30¦PetrieCH7.36 524.10¦524.1043769892 (yA + nValue)/tanPETRIE°
* Erosion/earthquakes
by time and attacks from treasure hunters affect future variations on Petrie’s
Casing Angle
R = (5^½
— 1)/2 Point B: by deductive
order: see The
G-point first
unitINCHES PETRIE MEASURED/calculated rJCR calculated Petrie formula/term*
——————————————— ——————————— ————
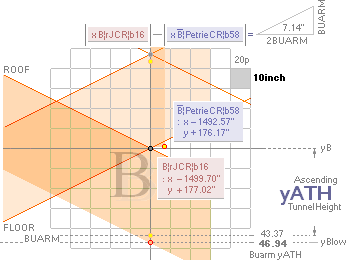
yA 172.90 ± 0.20¦PetrieCH7.64tab 172.91¦172.9045085255 yB
— (yBlimit = yConB + SIO)
xA 1517.80 ±
0.30¦PetrieCH7.64tab 1517.70¦1517.7016293661 xB
+ 18
* yConB = yPangle@H-end + yHangle@B-end = 3.0124757861’’
SIO = yConBoffset = nValue — D
The D part is
the dValue-projection
into a xyA-vertical;
The dValue is
trigonometrically calculated from the floor construction offsets — from the
G-point:.
R = (5^½
— 1)/2 Point G:
unitINCHES PETRIE MEASURED/calculated rJCR calculated Petrie formula/term
——————————————— ——————————— ————
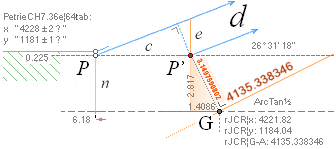
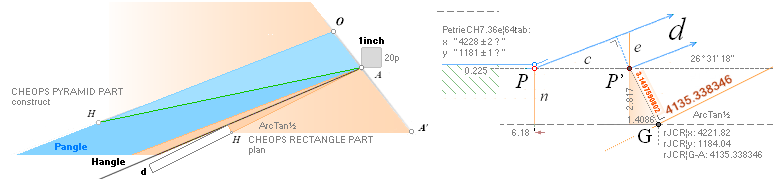
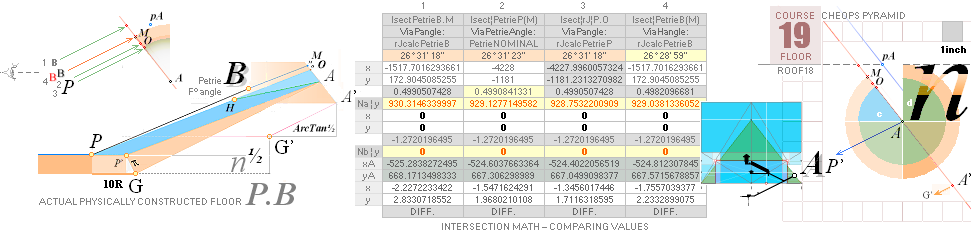
xP 4228 ± 2 ?¦PetrieCH7.36e 4228.00¦4227.9960057324 xG + 10R
yP 1181 ± 1 ?¦PetrieCH7.36e 1181.22¦1181.2240228242 yG — nValue = yG’ + nValue
1181.23¦1181.2313270982 The pi-version, also below:
The P°Angle 26°
31’ 23’’ ± 5’’ ?¦PetrieCH7.36e 26° 31’ 17.48’’¦(26° 31’ 18’’)? 26° 31’ 17.486086’’ *ForCA
lowest ?: 26° 31’ 18’’ APPROVED only with Petrie’s Question Mark
The H°Angle 26°
29’ ± 1’¦PetrieCH6.32e 26° 29’¦26° 28’ 58.55’’ Hangle*
* piVersions:
Pangle = ArcTan½ –
ArcTan(π/[AGdistance=4135.338346’’])
Hangle =
ArcTan½ — ArcTan(dValue/2yA(1,25)^½)
R = (5^½
— 1)/2 Point D:
unitINCHES PETRIE MEASURED/calculated rJCR calculated Petrie formula/term
——————————————— ——————————— ————
xP 2907.30 ±
0.60¦PetrieCH7.39 2907.38¦2907.3786302 *
yP 852.60 ± 0.30¦PetrieCH7.39 852.82¦852.8245796 *see also Queen Chamber Series
* Specific Simple GS-body
paragon intersections
with xLoAnom + bO/2 and xLoBnom
+ bO + 18/2
XLoBnom =
LowerBlineNOM ....... = ![]()
XLoAnom =
LowerAlineNOM ...... = b — P
xyAB = intersection point from LineAB, see Intersection Math unless already familiar.
THE D-ANGLES by deductive
order: see The
PG-point first — R = (5^½ — 1)/2
unitINCHES PETRIE MEASURED/calculated rJCR calculated Petrie formula/term
——————————————— ——————————— ————
(B’.pG)° 26° 12’ 50’’¦PetrieCH7.39¦46 26°
12’ 51’’¦26° 12’ 51.16 95 06’’ *ARCTAN
(2683R - 280R)/(F4 - 2456R)
* ARCTAN (1658.2 - 172.9)/(4534.4 - 1517.8);
Petrie gives no tolerance. He states
s39:
” This, when corrected for lower signal
being 3 too high, gives
26° 12' 50" for mean angle of
both passage and gallery together.”, and in s46:
”.. the step will be
61.1 long; and this at the angle
26° 12' 50" (by which the end
of the gallery was calculated from the plug-blocks) will be
30.08 vertically ..”.
(B’.D)° 26° 2’ 30’’¦PetrieCH7.38¦39 26° 4’ 31’’¦26° 4’ 31,22 09 20’’ *ARCTAN [yD—yB-yBlimit]/[xD—xB—18]
* ARCTAN (852.6 - 172.9)/(2907.3 - 1517.8)
26° 3’ 59.17 05 23’’ — Petrie gives
no tolerance:
— PetrieCH7.38 gives several
different angular values over the path B’.D ranging from 26° 2’ to 26° 7’. And
he states:
” .. it will suffice to say here
that the mean angle is 26° 2' 30" ”.
Trigonometric cross checking with
Petrie’s own specified lengths show some [minor] deviations, [still within the
Petrie given tolerances].
(D.pG)° 26° 20’ 26’’¦PetrieCH7.38¦PetrieDangles 26°
20’ 1’’¦26° 20’ 0.43 27 59’’ *ARCTAN (yPG - 1380R)/(F4 - 4704R)
* Never
mentioned by Petrie. See TP27.
— Petrie cogitates a section of
arguments without mentioning the actual [measured] angle. PetrieCH7.39:
” Hence we cannot say exactly what
direct relation the theodolite bore to the passage;
but we can obtain the angle of slope
very satisfactorily, by taking ..”.
— With the Petrie given length we
can cross check-calculate the missing part as described in TP27.
:
*See SCHEMATIC OVERVIEW and WHOLE NUMBER R MULTIPLES
F4 = PetrieCR¦b58 =
4534.1965759686’’ ¦ 4534.20’’ — PetrieCP¦bLOWEST
= 4534,15’’
— Because the B-PG
ascending construction line from The rJCR¦b16 Agent original has no actual physical
representation in the edifice — see from The Push — The Petrie B point [B’] — a FLOOR
preference — takes the actual physical construct reference. In order, as here
so understood, to secure a clear measuring sight line up to the Gallery south
end on that construct, the sloping Gallery Ramp floor must have a small BREACH
guaranteeing that no material covers a measuring sight line. This condition
means, InPetrieQuote
Col2 Row23, a slight BENDING at the D-point between
the two parts upper-lower along the ascending path: One smaller angle B’D, and
one larger angle D.pG with the mean on the whole path as B’.pG.
— But Petrie — in part: TP27 gives a full account — leaves out
some measuring data [on D.pG] which forces us to »recalculate AND CHECK
Petrie’s presented [angular] values» — with some minor but still acceptable deviations
within the Petrie given tolerances: no big deal.
— As we already have calculated the
basic reference points from the rJCIRCLE agents as The Petrie D-point [LinD], The Petrie B-point [LinB] and The PG-point [LinPG], these angular
comparing calculations — here — can use a more convenient grip: Whole Number R-Multiples — where these lie within the Petrie
given measures and their tolerances — simplify the comparing angular values
process.
— Petrie gives no direct
trigonometric formula for the angularly calculated results. So we just have to
”fill in” with the most simple of the Petrie given values, lengths, to check
and cross-check the valid results.
— The full account for these
calculations are given in the section TP27.
R = (5^½
— 1)/2 Point PG:
unitINCHES PETRIE MEASURED/calculated rJCR calculated Petrie formula/term
——————————————— ——————————— ————
yP 1658.20 ±
0.60¦PetrieCH7.46 1658.17¦1658.1652607385 [b1 — xB]/2 + yB — [ yATH + BUARM]
xP 4534.40±
0.25¦PetrieCH7.25 4555.88¦4555.8764838817 *b1 = rJCR¦b16
* SEE THE SEALING PUSH: The rJCR¦b16 agent’s calculated yP value through
its b=4555.88’’ is just hung on the PetrieCR¦b58 agent:
— The rJCR¦b16 agent is so only USED
to generate this yB-value — which origin effectively is hidden below bhOFFSET the Petrie pavement of the regular
Petrie Cheops Pyramid agent PetrieCR¦b58 = 4534.20’’. Unless familiar with the
two geometrical ideal pyramid agents, nobody will — ever — understand The Construction Plan: it will be a
complete enigma until revealed through the [»most simple»] rJCIRCLE complex.
PetrieCR: FigureCASINGS ¦ The TouristVersion ¦
COMPILED FOR UNIVERSE HISTORY 3Feb2020 — The full
Mathematical and Geometrical disclosure — ATLAS — of The Great Cheops Pyramid
from The 1883 measures by
the Flinders Petrie working group.
Compiled
short overview with links included to the actual detailing sections
RELATED
MATHEMATICS AND PHYSICS — FROM THE BEGINNING
HOW TNED EXPLAINS THE 1883 FLINDERS
PETRIE MEASURED CHEOPS PYRAMID
SEE
ALSO IN Introduction — SOME DETAILS ON THE OUTER FORM OF
THE GREAT CHEOPS PYRAMID
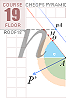
Begin — CHEOPS RECTANGLE:
With the mathematical geometry
thoroughly defined for the Golden
Section paragon (the GS-body), and The 1883 Flinders Petrie measured Great
Cheops Pyramid, as observed by the TNED rJCIRCLE, a first seemingly exact fit
appears between the two through The ArcTan½-line:
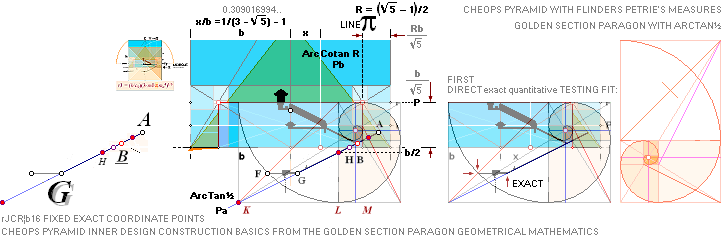
———————————————————
ENTER ¦ GS-body
— HOW IT ALL STARTED — PHASE
1 — THE CONSTRUCT
FOUNDATION LINE
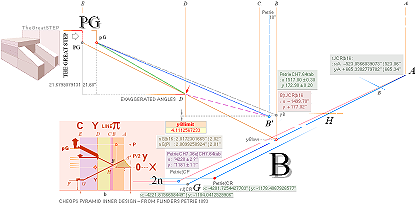
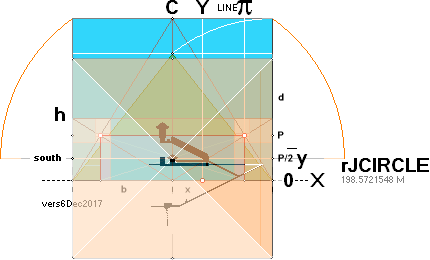
The 7 fundamental coordinate points K L M G H B A
along the entrance sloping ArcTan½ line are determined for further exact
Petrie measured quantitative comparing.
All calculations in this presentation are given through the main pyramid agent rJCR¦b16 with some support from the
ideal PetrieCR¦b58 agent.
— All vertical height values are
related to the Petrie given pavement.
The rJ-reference certifies — once and for all — that
no possible tracing to the origin will be possible UNLESS (correspondingly) TNED familiar: The rJCIRCLE is the guide.
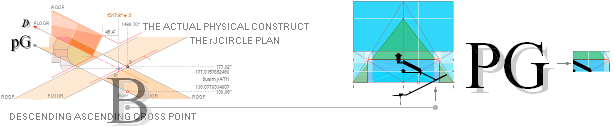
Concealed Construct:
PetrieCR ¦ HowStart
A Concealed Construction Plan — See pyramid agent
details in Introduction
— The two Pyramid Agents CR and rJ with the actual remaining
Cheops Pyramid (CP):
— The actual construction plan quantities
— however — is made from the rJ part relative the CP¦CR part so:
![]()
— All ideal INNER DESIGN GS-body Cheops Rectangle (CR) EXACT
numerical quantities — the whole plan — are reckoned with the rJ part’s
baseline on the Petrie pavement. Same vertical height reference as our two pyramid agents CP and CR.
Because the whole geometrical design
builds on two differently sized but perfectly uniform pyramid agents, the
design layout can freely dispose of either agent to GENERATE EXACT QUANTITIES.
In finalizing this layout, both pyramids share the same casing and top, but
have slightly different bases and heights: the larger rJCR¦b16 agent has its
base 27.58’’ below the Petrie pavement with a 2×21.67’’ broader base. The
resulting original layout so becomes SEALED, projected finally only on the
visual PetrieCR¦b58 agent,
corresponding to the Petrie measured PetrieCP Cheops Pyramid.
— Nobody will even come close to even
a clue to the original construction plan unless acquainted with the rJCIRCLE part [as in TNED].
![]()
The seal is realized by pushing [schematically
as illustrated] the CR-part into the rJ-part with the horizontal half pyramid
base offset difference (21.68’’) between them. All acquired values then become
safely hidden from any direct inspection — until someone enough motivated to
dig, deep [nuclear physics stuff, see from NatCH], discovers the plan.
Finally, with the rJ pyramid agent’s
baseline level situated (27.58’’) below the Petrie pavement, both pyramid agents rJ and CR now share one and the a
same original Cheops Pyramid top and casing.
All pyramid data is then lying
transposed onto the only visual remaining pyramid agent CR. It will be impossible to discern
as separate from the actual Cheops Pyramid edifice — as measured by Flinders
Petrie and his given tolerances.
Both CR and rJ agents have exactly the same casing and top. The only
difference is that rJ have a lower baseline — and the whole construct plan is
safely sealed inside the two — as one — as described.
SPECIFICALLY:
The entrance
point A — reckoned from the rJ agent — is/becomes directly
transposed ONTO the actual built Cheops Pyramid PetrieCR¦b58 pyramid agent.
Nobody will have the slightest clue, unless rJ acquainted. It will be a concealed riddle.
See also Petrie references [PetrieCH6.22] of the lower casing socket
measures in IntroTEFF
[all four corners with different
vertical ground socket sets between 23-40’’ below Petrie’s pavement].
Such an edificial planning obviously needs some real steel sophisticated
tools.
See detailed IntroEX quantity
examples from QUEEN’s CHAMBER: How the rJCIRCLE Golden Section Cheops Rectangle complex forms
the Cheops Pyramid basics within the Petrie given values and their tolerances.
The description continues from there
with overviews and detailed descriptions of the different sections, and how
they are calculated in their approved quantity equivalence with the Petrie
given measured values.
The rJCIRCLE complex is explained
from the beginning from NatCH.
— All section after explain the
different details.
Summation
In all (4Feb2020):
— The GS-paragon Cheops Rectangle specified
as the main constructive pyramid
agent rJCR¦b16 determines
provably by quantities the corresponding measures specified by the Flinders Petrie working group
in his 1883: The geodesically measured The Great Cheops Pyramid. The corresponding
quantities prove the connection.
IntroTEF: PetrieCR — An
introduction to
HOW TNED is connected
to THE 1883 FLINDERS PETRIE MEASURED CHEOPS PYRAMID
Introduction
— see also further Petrie data At
the built precision
DETAILS ON THE OUTER FORM
SOME
BASIC DETAILS ON THE OUTER FORM OF THE GREAT CHEOPS PYRAMID SHOULD BE FAMILIAR;
SCHEMATICALLY:
— The
leftmost below schematically iconic drawn figures
represent
the only remaining ”The Cheops Tourist Version”
that
is left for us to visit:
remnants
of The Great (ancient named Greek Cheops) Pyramid.
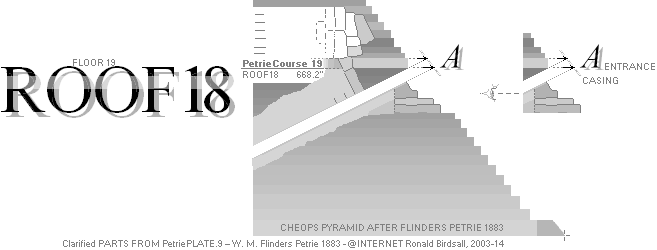
PetriePLATE.11 shows a drawing of the pyramid’s
”CASING-STONE IN AVERAGE CORNER SOCKET”, partly iconized below.
— The term here ”casing overlay”
refers to the vertical and upwards additional masonry over the remaining casing
stones that we safely can assume once were. Documents tell about the great
earthquake period in Egypt (late 1100) after which the casing part of the
Cheops Pyramid masonry was removed to rebuild Cairo.
The unevenness with partly eroded end
blocks in the pyramid staircase masonry gives no direct precise information of
the vertical casing overlay metrics (roughly 1.6 M from PetriePLATE.9).
No other known specification of this
parameter has been found in Petrie’s work from 1883 on The Great Pyramid. Or that such
information exists, but is not directly easily recovered.

— The remaining casing blocks
(PetrieCH6.29, ”.. the remaining casing stones on the
N. base”) are said to be of order ”few”.
— With some help of further
photographic documents @Internet 26Dec2019, they seem to be situated on the Pyramid’s
North mid side, below the pyramid entrance. (All other remnants of these casing
stones, if any on the other pyramid sides, are badly eroded).
— Base and Angle. That is the outer
formative basics reported from Flinders Petrie (1883).
— Our comparing agent is The Golden
Section — the ideal simple Cheops
Rectangle Geometry.
As is stated by Flinders Petrie (PetrieCH6.24) ;
— The average measured value 51°52’ ± 2’ of the sloping
angle of the remaining pyramid walls was taken (preferentially) from the north
side measurements along the slope of the pyramid’s remaining — partly eroded
staircase masonry. (The eroded parts makes a more precise [small scale] measure
out of the question).
THE
CASING ORIGINAL
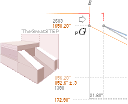
Figure b: The ”Tourist
Version”;
— Pyramid staircase masonry. Partly in
bad shape, with a few remaining casing stones at the north
side of the pyramid base. The average slope value specified by PetrieCH6.25 of
the remaining staircase masonry is
51° 52’.
— For the vertical and upwards casing
overlay, we only have a relative value based on a PetriePLATE.9 drawing
showing approximately
1.5(59’’)-1.6(63’’) M at the base.
Figure c: The
TouristVersion’s actual Petrie measured version.
— This is the actual Cheops Pyramid we
find in the Flinders Petrie based measures.
Figure a: Petrie’s
Pyramid base in figures bc taken directly on the Petrie partly, see PetrieCH6.24, measured
casing stone slope value
51°49’.
— It is practically identical with The Golden Section and Cheops
Rectangle slope value angle
C° = 51°49’ 38,2525’’ = ArcTan (h/b =
1/√[R=(–1+√5)/2]) = 51.82 729 237°. Also in PREFIXxSIN: ArcSin R = C°.
— However: No definite direct Petrie
given such value exists — presumably partly due to uncertainty issues on only
the few remaining casing blocks (also partly ”owing to irregularities”).
— The figure a-type then, will be our
only possible EXACT GEOMETRICAL candidate in any explaining ATTEMPT of the
whole Cheops Pyramid complex — from the TNED point of view: the actually obtained rJCIRCLE and its claim of enveloping the
whole Golden Section Construct.
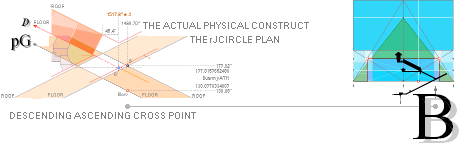
Figure d: The actual rJCR¦b16 Pyramid Agent;
— Just the vertical — 27.58’’ below Petrie’s Pavement —
elongation of a:
It is the rJCIRCLE¦b16 CONSTRUCTION
version — here to be tested.
NatCH: Continued Description ¦ The Device
(Sw.ed.
CUV-analysen
CHEOPSPYRAMIDEN
UTMANAR VETENSKAPSSAMFUNDET)
The rJCIRCLE
Complex — OVERVIEW in short: See INTRODUCTION
NATURE CHALLENGES MODERN ACADEMY
(1800+)
—
says TNED. We examine the statement.
In deep.
NATURE CHALLENGES MODERN ACADEMY
THE CHEOPS RECTANGLE — From Mathematics
5 basic Laws — The
Cheops Pyramid (Petrie
1883)
The Cheops
Pyramid Paragon from The Golden Section — by exact Geometrical Mathematics:
See also unless already familiar GOLDEN SECTION ARITHMETICS
GOLDEN SECTION EDIFICE — how the
unique bd=h² pyramid triangle appears:
The Golden
Section constant R=(√5 –1)/2
with its paragon-morphological geometry shows us directly where any significant
intersections appear in the corresponding geometrically unique Cheops
Rectangle bd=h² triangle; Its tangent and slope
ArcTan[h/b=√(2/[–1+√5])=1,27201965]=51.82729238°
= 51°49’38.25’’. With a
transparent overlayed section as seen from above along with a ground spotting
westerly view ahead as seen from the rising sunny east side, the center of the
construct appears as the Cheops Pyramid in illustration above:
— All thorough
dimensions here are derived from Flinders Petrie Sources
@Internet in his (1881-1883)
measuring works on the same so called The Great (ancient Greek: Cheops)
Pyramid. Precise data with quotes from Petrie will be frequently referred to in
this presentation.
How it all started — basic geometry illustrated
— Just a simple innocent test that
suddenly
 — Wao. Is that really so, simple?
— Wao. Is that really so, simple?
brightened up on its surprisingly
simple direct result:
— GS-R =
(√5 – 1)/2 = 0.618033988..; (rJ[mJ=5.975T24KG]=7817.80’’)/100R = √16000.9..; (PetrieCP¦b=4534.40±0.25)’’/rJ
= 0.58000..
FOUND STUFF. Faulty statements are not allowed
here.
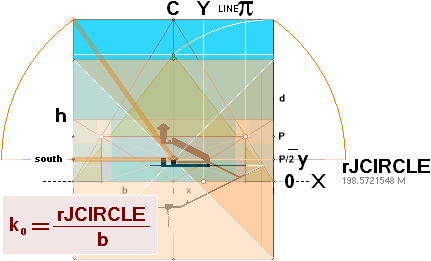
FIRST BASIC: rJ = 198.5721548 M =
7817.80’’ — See constants in HOP.
Adopted more
precise mJ value from the ideal rJCR¦b16 value 4555.88’’:
mJ
= 5.9744931448 T24 KG from rJ
= 198.5665397062 M = 7817.5803033942’’
CENTRAL CONSTANTS: u, m(n),
m(e), h, c0 as given from the Instrumental
Epoch (IE 1960-1999) HOP
section.
The rJ-equation expresses the radius
of a Dmax compact TNED N3m20
deduced neutron body with the mass of the Earth
mJ=5.975 T24 KG, a sphere
with a (Dmax) density of
1.82 T17 KG/M³.
That is a sphere precisely as
illustrated NatCH:
— a circle enveloping the d-corners
of the Golden Section ¦ Cheops Rectangle:
The rJCIRCLE center/origo is situated in the intersection C¦y.
With PETRIEb=4534.40’’ and rJ=7817.80’’ the relation
is
PETRIEb/rJ = 0.580009271
and the relation
rJ/100R = √16000.9049099833.
— That is how it all started: WE
BEGAN TESTING THE SIMPLE NUMBERS FOR (ev.) EXACT FITS.
— Testing the
precision, we adopt the two ideal Cheops Rectangle (CR) Geometries for
PetrieCR¦b58
.......... 58R√16000 = 4534.196576
~ 4534.20’’:
—
The actual ideal Flinders Petrie Cheops Pyramid with its ideal Cheops
Rectangle casing;
IDEAL: rJCR¦16 = 100R√16000 = 7817.580303’’
k0¦GS = √[(0.5+2/√5)²+1] = 1.7159333294 = rJ/b ; b:=rJCR¦
b16=4555.88’’;
rJCR¦b16
................ rJ/k0 =
(100R√16000) / √[(2/√5 + 0.5)²+1] = 4555.876484 ~ 4555.88’’.
— EXACTLY The Same as the
b58-pyramid, but with its pyramid base situated slightly below [27.58’’] the
Petrie Pavement zero height reference.
Basics as calculated from the
rJ-value in NatCH.
PETRIEb
................. 4534.40’’
± 0.25
The comparing 1883 Flinders Petrie
measured Cheops Pyramid’s half base on its determined pavement as the
established Petrie zero height reference.
We use the
abbreviations
PetrieCP
.................. for Petrie given measured values on the Cheops Pyramid (CP)
PetrieCR
.................. for corresponding
IDEAL Petrie Cheops Rectangle (CR) — GS-body — values
PetrieCR refers the PetrieCR¦b58 value
4534.20’’ while PetrieCP refers
Petrie’s own measured values: 4534.40’’ ± 0.25.
The three
following iconic
CHEOPS PYRAMID
COMPLEX ILLUSTRATIONS
will help in
navigating the (tight) description:
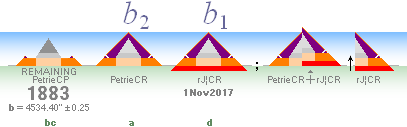
PetrieCP PetrieCheopsPyramid:
Petrie measured the average slope of the pyramid staircase masonry as 51° 52’ , with a more
narrow particular casing stone slope of 51°49’ on the remaining few stones at the
pyramid base;
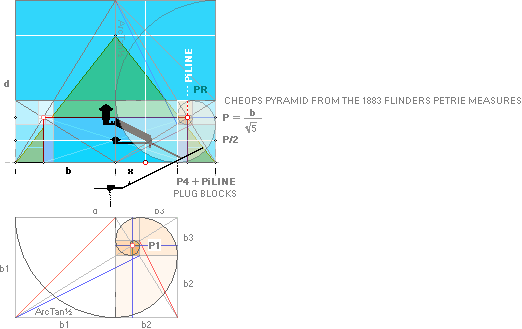
PetrieCR PetrieCheopsRectangle:
With the pyramid’s half side PETRIEb=4534.40’’
± 0.25 on Petrie’s
casing slope, ideally the same as the ideal Cheops Rectangle slope
51°49’ 38.25’’ we obtain a broader and higher top pyramid enveloping Petrie’s
staircase’s 51°52’ masonry.
— If we test the 0.58 candidate for this purpose we find a corresponding
PetrieCR¦b58 = 4534.20’’ — well within the given tolerance interval with
its lowest 4534.15’’ — with the
help of the near rJ-spouse and its ideal EXACT
rJ = 100R√16000 = 7817.58’’. And where NOW we have
PetrieCR¦b58 / rJ¦16 = 58/100 giving the new PetrieCR¦b58 =
58R√16000 = 4534.196576’’ ≈ 4534.20’’.
rJ¦CR The enveloping MASTER
Cheops Rectangle — exactly the same top as PetrieCR, but lower, beneath the
Petrie Pavement with an additional 28.48’’, as calculated separately.
While Petrie’s
Cheops measurement have no fix and stable preference except the Petrie measured
Cheops Pyramid base (4534.40’’ ± 0.25) and the mean staircase masonry slope (51°
52’ ± 2’), the two new
testing envelopes PetrieCR and rJ¦CR do have such properties.
What does that situation suggest?
The situation suggest that IF the pyramid
was intended as such, these two solid preference guiders and a marker WILL
define a clear reference where Petrie’s measurement WILL coincide — practically
excellent perfect — or not at all. That will be our test.
— We have
already seen that there (already) is a profound VISUAL fit in the simple
geometric paragons. But how close is it, and what can it clarify, and
elucidate?
See a Continuing
Description after the
below describing linked passages.
ALL ABOUT WHAT THE ENTIRE COMPLEX IS
FOUNDED ON.
INTRODUCTION: NatCH
Nature
challenges MAC
INTRODUCTION TO NatCH — rJCIRCLE
Response
A
FULL QUANTITATIVE CONSTRUCTION LAYOUT PROOF
Additional
basic terms and meanings in HowStart and The GS-body
A
full quantitative proof has been found/clarified (10Jan2020):
Statement:
A
DEDUCTION is asserted to be absolutely EXCLUDED to the inner Cheops
Pyramid paragon structural DESIGN
The Golden Section paragon body
Proof:
without the rJCIRCLE
Cheops Rectangle as a fixed no
tolerance quantitative index by exact geometrical quantities: fractions,
roots (pi + natural physical constants [Planck constant]).
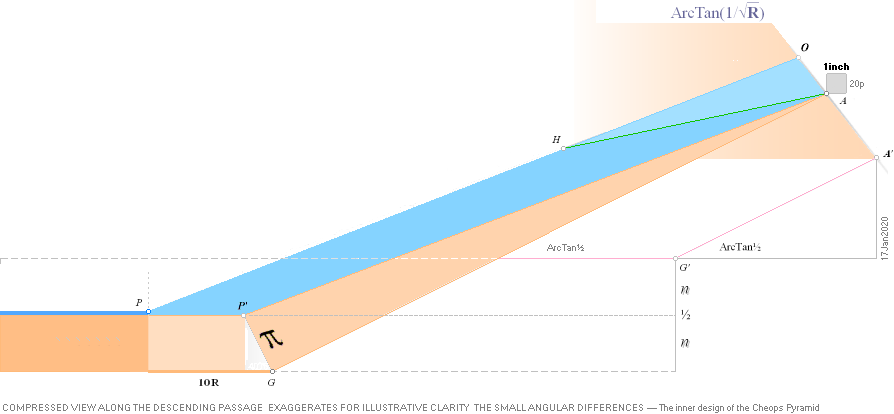
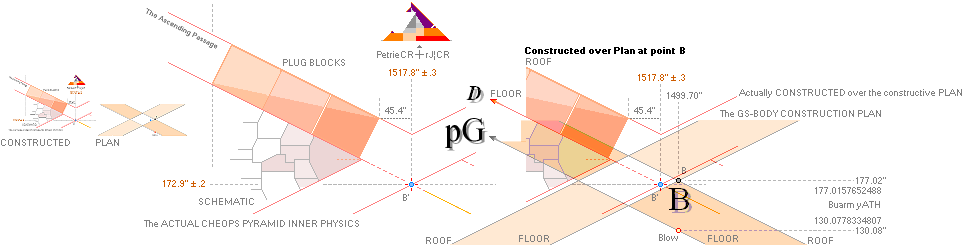
bOFFSET: bNOM
»THE CHEOPS
RECTANGLE PYRAMID OFFICE» AND ITS
TWO PYRAMID AGENTS — HowSTART
b1 — b2 = 21.68’’ = bOFFSET
b1 = [rJCR¦b16 = 100R√(16000/[(2/√5 + 0.5)²+1])] = 4555.876484’’]
b2 = (58R√16000 = 4534.196576’’) The Petrie Cheops Rectangle Pyramid Agent PetrieCR¦b58 = 4534.20’’
b1 — b2 = 21.6799079131’’
:
The GS-body paragon is applied on the
slightly larger same top rJ Cheops Rectangle rJCR. Its 27.58’’ higher/deeper
Cheops Rectangle bd=h² pyramid is then pushed vertically the same 27.58’’ up to
the basic pavement Petrie level — and an additional half pyramid base offset
21.68’’ South to North INTO the
corresponding ideal Petrie Cheops Rectangle Petrie¦CR.
Result: Both pyramid agents now have the same base and casing properties
as the (for our quantitative test the remaining) Petrie measured Cheops Pyramid
Petrie¦CP;
— All measures are now with respect to
the Petrie height zero preference, the Petrie pavement platform.
— These arrangements establish the
construction plan quantities. The end picture shows the two pyramid agents
rJ¦CR with one and the same pyramid top and casing, where rJ has a 27.58’’
lower and 2×21,68’’ broader baseline situated below Petrie’s pavement: the CR
agent’s zero level.
Bottom line:
— Guaranteed no one will be able to
deduce or even imagine a clue to the construct unless rJ familiar. The edifice
stays buried in a riddle, an enigma, until acquaintance is established.
— The
rJCIRCLE¦GS-body quantities are (constructively) flat Petrie pavement
pushed into the inside of the actual Petrie¦CR-pyramid. The result becomes an indexing CONSTRUCT
for the 1883 actual Petrie measured Cheops Pyramid Petrie¦CP — proved by the
corresponding quantities: the rJ agent defines Petrie’s measures.
CONTINUED
DESCRIPTION: Introduction ¦ NatCH
The
illustration below collects the basic main geometrical visual image concepts:
What we need to advance, further.
THE GOLDEN
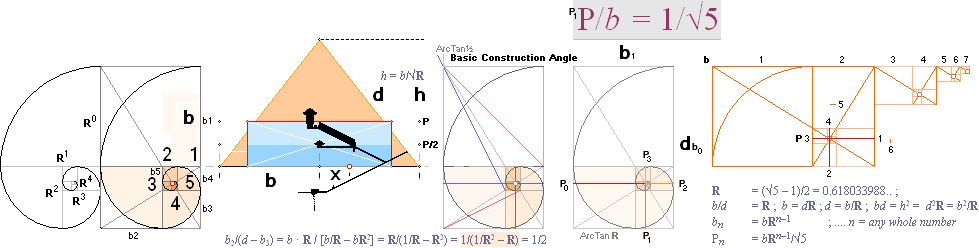
SECTION BODY — ARITHMETICS — ArcTan½LINE — The GS-body — NatCH — The Golden Section
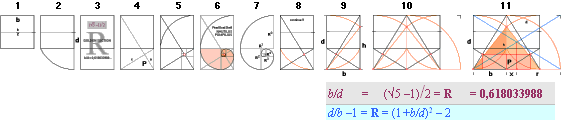
Relation R = b/d = [√5 –1]/2 = 0.618033988:
GOLDEN SECTION EDIFICE — how the
unique bd=h² pyramid triangle appears:
Leftmost [R1↓,
R² → , R³↑, etc.]:The Golden
Section’s sectionally smaller squares with its quarter inscribed
circles are built up as in an exponential series of the form
R^n with R=[√5
–1]/2. n denotes whole numbers only, beginning from n=0 giving a unit
1 = b = Cheops Rectangle triangle/pyramid’s half base.
Rightmost: Its [partial,
almost exact] resemblance with the Nautilus
Pompilius ”Pearl Boat Shell” (sw. Pärlbåtssnäckan).
It is here denoted with a corresponding
P for each consecutive [See deduction in GSbody]
Pn = b·R^[n—1] /
√5. Each Pn is the actual normal [right angle] distance from the
PearlShellEyeCentre to the GS-body envelope.
— All these definite geometrical
quantities — exact measures — are our tools for analyzing and investigating any
coupling between the GS-body and the 1883 Flinders Petrie thoroughly measured
Cheops Rectangle. [Some authors name it Khufu
Pyramid — after Modern Academic ideas in concern of an academic consensus of
suitable origin].
— GENERAL with b=1:
bn = R^[n—1]: The
Pyramid half base b1= R^0 = b. Next smaller GS-divided
square is R^1 for b2, then R^2 for b3, etc.
— NOTE THE [50
M] DEEP WELL-TUNNEL NOT DRAWN OUT HERE with the so called Grotto in the middle
[The Cheops Rectangle Circle origo — Latin:
origin, not found in the English dictionary — from where the geometrical
construct is made]. Petrie [Quote] gave no measures
because of its uninviting feature. And nobody else seems to have: no specified
measured quantities are known here. Different sources give different ideas of
the actual path. See Help
ILLUSTRATIONS.
— Quest:
Is there any report from Egypt 2 500 B.C. that they knew about the Golden
Section body ([5^½ –1]/2)^n structure?
A
specific search @Internet 1Jan2020 on »golden
section in ancient egypt» gives at least one PDF-based clarifying source
titled
WERE THE FIBONACCI SERIES AND THE
GOLDEN SECTION KNOWN IN ANCIENT EGYPT?, by Corrina Rossi and Christopher A.
Tout, 2002:
” The conclusion is that concepts such as ϕ and the convergence to ϕ have little in common with the surviving
ancient Egyptian mathematical documents and that they are quite far from the
ancient Egyptian mentality.”; The PDF-source text sometimes misses an ”i”, here marked below:
” As for the first point, it
might be suggested that the Egyptians had a geometrical concept of φ,
just as the Greeks had a geometrical concept of π, and that they tried to
approximate it using an infinite sequence of fractions. However, the first evidence of a geometrical concept of the Golden Section is to be found in Euclid’s Elements,
dating to the third century BC (Fowler 1982), about 15 centuries after our
Middle Kingdom scribes compiled their documents. No
ancient Egyptian mathematical source contains any element which may be
interpreted as pointing to an earlier knowledge of φ.”, p113mb.
There you go.
FONT NOTES: ϕ ϕ: definitely so drawn in the source text — but definitely so φ
φ written when imported and converted by a Unicode Note Pad:
— The text source gives no mentioning.
Dictionary Greek Alphabet (Swedish Lexicon) shows Φφ for our letters
F f (sw.”fi”, eng. ”phi”): Microsoft WORD (Ctrl+Q, Font SYMBOL) shows![]() , the latter sign apparently the same as in
the quoted source text, not mentioning what the spell is supposed to be (it forces us to do what we don’t want to do: speculate
on the content: ”we suppose they mean a
small F”).
, the latter sign apparently the same as in
the quoted source text, not mentioning what the spell is supposed to be (it forces us to do what we don’t want to do: speculate
on the content: ”we suppose they mean a
small F”).
MathNote: Conv. ”Fibonacci series” include a more general outlook than
only our ([√5 –1]/2)^n structure
in this subject — but ”modern sources” seem not overly interested in presenting
the strict geometrical Golden Section paragon as we do here (in connection to
the Cheops Pyramid).
— What’s your point?
— IF the
Egyptians didn’t know our ([√5 –1]/2)^n structure in
this subject, who built
the fit?
Check the correspondences.
— What is our
mission?
— To TEST and
look for CLUES — as IF the Constructors had taken this stand:
— As clear,
simple and straight as possible (5·8 + 18 = 58, etc.):
— Use NatCH the GS-body to RETRIEVE — recall — the way WE made the
inner design: Try to find MATHEMATICALLY
EASY — spelled: easy — PROVABLE reference points with which to control, test
an check exact corresponding Petrie measures in a general quantity test.
We use two separate CalCards (TableA and
TableB) organized as the one in The Result Table;
COMPARING VALUES:
We use TableA (rJCR¦b16-results) to
fetch corresponding values from TableB (PetrieCR¦b58-results).
— With this arrangement we can
easily and directly receive readouts (type: [G5+TableB.G5]/2) by a two party
based average result — or other: We can easily test any [other] b-value agent
as well.
— What The F-Word is a ”calCard”? It is just a more
associative This Author’s term for [conv. spreadsheet, SS] a Computer
aided Calculating Program:
— A ”specifically
tagged calculating card” with specific reference capabilities — in the form
of individual programmable cells collected in [rectangular] separate blocks;
— A smaller
or bigger section of a programmable active spreadsheet. Type @Internet free
OpenOffice
— My idea of
the term came from MsWORKS 4.0 [Windows 3.1] where a LINKED part of a SS could
be imported to a word processing program: Along with text, it appeared as a
separate iconic CARD. By clicking the Card, it became active and
editable/usable [classic Object Linking and Embedding]. It was in the beginning
when [high speed turbo assembler] computer programming still seemed open AND
FREE to Windows customers.
FIRST MOST
SIMPLE AND DIRECT: 31Dec2019 ¦
FirstSimple: GS-body ¦ R-constant
FIRST SIMPLE OBSERVATION
A FIRST quantitative
GALLERY TEST — from the rJCIRCLE fit.
Apart from the
first obvious results in (Sw.ed.) CHEOPS
REKTANGEL TabTest (Nov2017):
A First
APPROVED MEAN AVERAGE FROM THE TWO PYRAMID AGENTS
Ref.: BPOINTMain:

In determining
the B-point as 1 of The 7 fundamental
Golden Section ArcTan½ Line points,
there are two
GS-type fits: LOWER and UPPER visualizing a direct fit in the ascending
passage’s breadth.
— The
yB-difference of these is yATH with a yBlo =
yB — yATH.
— Calculating the
ArcTan½ slope where it intersects the Pyramids mid vertical in Point
PG from yBlo, and using our Two Pyramid Agents respectively, we find their averaged mean
on the vertical Pyramid centre to be
1657.78’’.
MEAN AVERAGED RESULT ![]() : FIRST »SIMPLE» OBSERVATION
: FIRST »SIMPLE» OBSERVATION 
1658.20’’ ±
0.6, lowest 1657.60’’.
— Approved.
Below is related even a more precise-near (1658.17) Petrie nominal value (1658.20).
— See also the ROSSI2002 reference:
— The ancient
Egyptians hardly knew the math — as we understand it.
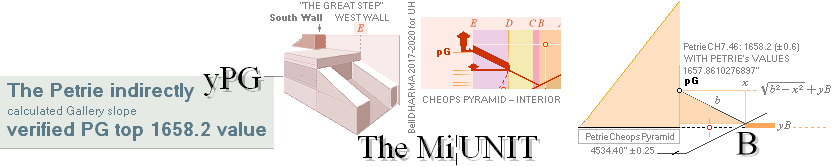
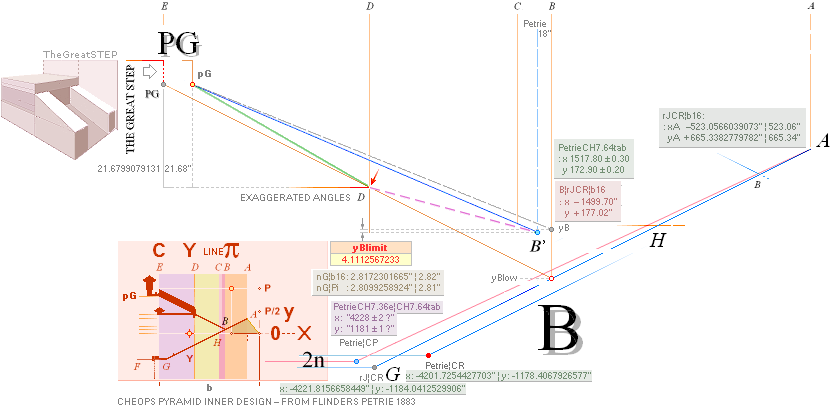
PETRIEpG: yPG ¦ FIRST ¦ pGconBuarm ¦ yConBUARM — calc.1658
THE GREAT STEP — Cheops Pyramid
Gallery ramp top,
— See also THE LOST ANGLE.
Petrie does not give the direct ypGallery
value 1658.20’’ ± 0.6. Its
figure appears only through Petrie’s two specified components at The Great
Step, up at the south end of the so called Grand Gallery part.
PetrieCH7.46:
”.. the height of the step face is 34.92 or
35 on E. ..”
”.. the step surface at
the E. side of the S. doorway is 1693.2 ± .6 over the pavement.”;
— We calculate the difference as
1693.2 — 35 = 1658.2 (± 0.6)
(Some early @Internet picture photos show a
severe injured site).
rJCIRCLEcalc.:
yPG: Actual yPG math ¦ PETRIEyPG
It is clear that the rJCIRCLE Cheops
Pyramid construction plan has used a TRANSPOSITION EQUIVALENT
THE GALLERY-B-ENTRANCE-COURSE
19 CONNECTION
— same recurring constants at 3
different sites — between the B point (at ascending-descending) and the PG
point (at Gallery ramp top) and the 19th course level and its thickness (TCA) of the form
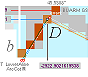
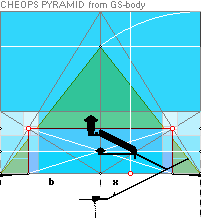
GALLERY RAMP END GREAT STEP 3D
drawing — Here FAIRLY RECONSTRUCTED FROM GIVEN MEASURES
———————————————————————————————————————————————————————————————————————————————————————————————
yATH ¦ BUARM
¦ yBlimit ¦ yPonB ¦ Fangle ¦ yBarm ¦ MiUNIT=100R ¦ bOFFSET ¦ 18
AT PG: yPG + 50R
+ yBlimit =
1693.1782168993’’ rounded 1693.20’’. Same Petrie identity.
AT PG: 50R + yBlimit =
35.0129561608’’ = 30.9016994375 + 4.1112567233. Same.
AT PG: yPG = [(rJCR¦b16=4555.88’’) — xB]/2 + yB — yBarm = 1658.1652607385 → 1658.17’’
→ 1658.2’’. Same.
Same. 3 different regions with the
same used exact constants — defining Petrie’s measured values.
All the values
mentioned by Petrie at the Gallery ramp top are rJCIRCLE-calculated-identified
constants from the rJCIRCLE complex calculated B point.
The same
rJCIRCLE complex B point calculated quantities are used to define the thickness
of the Petrie measured 19th course at the level of the casing entrance, and the
(TCA)
trigonometric/optical projection (Petrie19thProof) between these connecting the 19th course
with the sloping angle of the descending passage.
— We underline
here:
— This whole
expedition is completely based on the 1883 Flinders Petrie working group measuring results. Through
them only we (MISSION) SEEK
corresponding clues, hints and leads to verify A The Most SIMPLE GS-body geometrical — exact — mathematical
Origin, if at all. (No fancy creativity = zero speculation = zero doubt).
See also on The MiUNIT.
TGS: PETRIEpG —
TheGalleryTES
— GalleryTop:
Cheops
Pyramid data from Flinders Petrie
THE
GREAT STEP
THE GALLERY TOP
END SLOPE 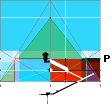
— yP(¦PetrieCR¦b58) = b/√5 see GS algebraic arithmetics
CHEIOPS
PYRAMID GALLERY SOUTH END
THE GREAT STEP — and its Gallery Top
WITH
VALUES FROM FLINDERS PETRIE 1883
A
full Petrie value corresponding rJCIRCLE calculated comparing description
of The Cheops Pyramid Gallery
is
given in these sections:
• CLARIFYING PETRIE POINTS ON THE GREAT STEP
• THE Abstruse Conic GALLERY HEIGHT
PetrieCH7.46 gives no other information than this:
”.. and
its lower edge is therefore at half the height of the gallery, that varying
from
167
to 172.”:
167 +
172 = 339’’ — an averaged Petrie mean value for the Gallery vertical height
with no further specifications.
Wikipedia (The Great Pyramid) gives a value
8.6 M
= 338.58’’. But its source is (here) unknown [See Miatello2010]. We have no further relatable references.
— Our
Golden Section paragon body (although rough) gives [ProvDETill] a close (7.5pixel) value on the scale
4534.2’’/100pixels: 7.5(SCALE) =
340.065’’.
PetrieCH7.46 In Quote Row1
neither gives guiding tolerances.
— But
the rJCIRCLE complex gives more precise information, see links above —
to be tested when and if more precise Cheops data appears.
yPGcalc: yPG
Petrie’s indirectly affirmed 1658.2 yPG
value
— by trigonometric details in PINver1658:
——————————————————
TP27 ¦ PINver1658 ¦ PetriePG
yPGcalc¦rJ: FromB
OVERVIEW
Cheops Pyramid after Flinders Petrie — SEE BEGINNING FROM THE CONSTRUCT
FOUNDATION LINE
THE yPG GALLERY POINT CALCULATION
SEE
ALSO COMPILED THE CONSTRUCTatB and THE TRANSPOSITION
and the KingEquivalents
The rJCIRCLE complex calculated Gallery pG¦PG point connects GcoW2 to the Petrie central northern Pyramid entrance’s Cheops
Pyramid 19th masonry course. That
is In Quote PetrieCH6.31 Row4 from where
Petrie deduced his (TCA) method with some help from ”the other Pyramids” to settle and measure
the entrance parameters. The inner design measures and quantities all depart
from and connect to that onset, as also here is accounted for.
—————————————————
rJCR¦b16 ¦ xyB ¦ yBarm ¦ B point ¦ PetrieIndirectlyVerified1658 — how the rJ
calculation defines Petrie’s measures
THE Cheops
Pyramid Inner Design CONSTRUCT IN SHORT:
— The
GS-body ArcTan½-line defines a set of 7 fundamental points (TCFL). From complementary additional GS-positions,
intersection coordinated results define all further quantities. The 1883
Flinders Petrie measures are the finders guide.
GalCalcOW — 1: GCOW2
GALLERY CALCULATIONS OVERVIEW part 1
The Gallery PG(pG) point is calculated from The B point through the two GS-body
Pyramid
Agents rJCR¦b16 and PetrieCR¦b58.
All quantities in this presentation have been deduced in
guidance under the 1883 Flinders Petrie measured Cheops Pyramid values from the
rJCIRCLE complex.
The yPG point quantity
appears from ENTER the GS-body primary PHASE 1 Result Table determination of the different
basic points on the ArcTan½ line at point B.
The descending entrance tunnel floor B-point is
calculated from the UPPER-GS position (B upper roof) and its intersection with the
given basic ArcTan½ line. The corresponding B-Lower point
results from the corresponding LOWER-GS position (B lower floor). The
vertical difference between these through the primary B-point defines the yATH- parameter — with further.
All these
values are calculated from the agent rJCR¦b16.
Additional
values from the agent PetrieCR¦b58 is then utilized with the b16 agent
to generate fix constants between the two bOFFSET slightly different agencies: We
take advantage of the difference between their horizontal coordinates which
gives us a set of basic constants:
yBlimit = yConB + yConBoffset = yConHBALimit
= yConB + SIO
yConOFFSET ¦ yConBUARM ¦
With these fixed exact calculated GS-constants we arrive —
at first — at a practically direct vertical hit (1658.17’’) on the
corresponding Gallery south sloping top floor point yPG within the Petrie given tolerances (1658.2’’ ± 0.2).
At second (and
third): these constants also connect to the entrance constructive quantities
and their Petrie mentioned importance at the 19th course, see In Quote PetrieCH6.32 Row11.
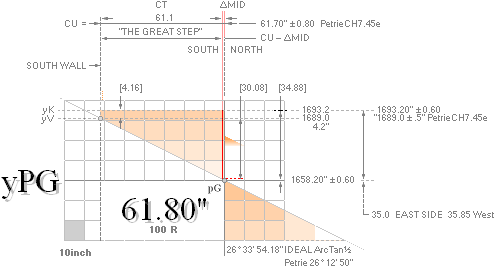
The Great Step — detailed: The MiUNIT 61.80’’ = 100R
PetrieCH7 mentions the 61.7 value (± 0.8 or ±
0.9) 5 times:

With a broad given Petrie tolerance
± 0.8’’ we easily identify a specific Golden Section Cheops-MiUNIT:
S = 100R =
61.8033988..’’ rounded 61.80’’.
The reason GalleryTop for our
illumination of the S=100R=61.80’’ unit here is simple
+ [(PetrieCR¦b58 = 4534.20’’)/√5 =
2027.76’’ = yP]
— [(S=100R=61.80)/2 = 30.90]
— [GalleryHeight = 338.76’’]
= 1658.2’’ = yPG as calculated from rJCR¦b16
Collected Petrie
data on TGS: CLARIFYING
PETRIE POINTS
The south end
Gallery ramp Step Face with its top floor King’s Chamber level south following
S=100R-value
marks the
transition from north to south
— »EXACTLY» in
the pyramid’s midpoint vertical as described by Petrie In
PetrieCH7.46 Quote Row30 Pyramid Mid.
— See The
yPG Calculations.
26° 12’ 50’’ PetrieCH7.39 In Quote Row34, ”mean angle of both passage and gallery
together”.
CU Adopted CheopsUNIT 100R = 61.80’’. See Petrie’s
5 quoting places of 61.7 ± .8.
CT PetrieCH7.46 In Quote Col1
Row22 partly
differently East side diverging value at site.
ΔMID PetrieCH7.46 In Quote Row30 ”.4 ± .8
S. of the Pyramid centre”.
34.88 ¦ 4.16 PetrieCH7.46 In Quote Col1
Row37; ”34.88 — .64
— 30.08 = 4.16”, ”say ± .2”.
30.08 61.1 · Tan(26° 12’ 50’’) = 30.083332661, PetrieCH7.46 In Quote Col1 Row37.
34.88 measured (mean) step face height in In PetrieCH7.46 Quote Col1 Row34.
Petrie’s given tolerance ±0.2 with
34.88 allows max 35.08: we are allowed to adopt a 35.013 as below.
yV 1689.0 Petrie’s
(measured/calculated) virtual sloping floor end at S. wall.
yK 1693.2 1689
+ 4.16 = 1693.16 → 1693.2 ”± .6” In PetrieCH7.46 Quote Col1
Row42.
35.0 Adopted mean from PetrieCH7.46 In Quote Col1
Row18; rJequiv. 50R + yBlimit = 35.01295616 rounded 35.013.
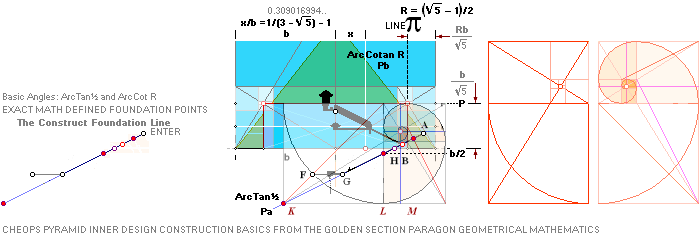
PHASE1: — The 7 Points Construct Foundation
Line ¦ Jan2020 ¦ PHASE2 ¦ ENTER ¦
SEE
SHORT INTRODUCTION IN NatCH
PHASE 1
Quantitative
Determination of The Basic Properties
THE FOUNDATION LINE CONSTRUCT
The CONSTRUCT FOUNDATION LINE
THE 7 FOUNDATION POINTS — K L M G H B A
TABLE OF
RESULTS Jan2020: — THE 7 FOUNDATION POINTS — K L M G H B A
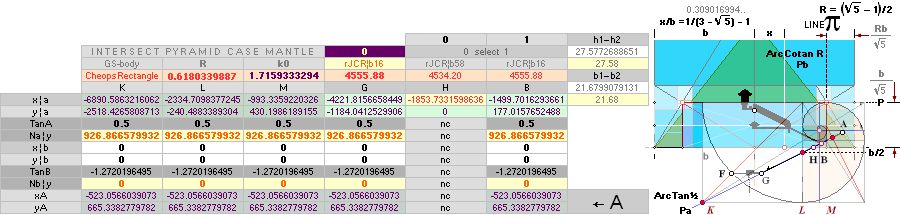
This table of resulting quantities define
all the points lying on The ArcTan½ line in its
intersection with the ArcCot √R line — the actual Cheops Rectangle ideal
casing surface slope C° = 51.82 72 92 38 = 51° 49’ 38.25’’ from the Golden Section paragon geometry.
BASED ON A
PRECISION OPTICAL QUANTITY MEASURE by Flinders Petrie in (publ.) 1883
we use the
mathematically well defined GOLDEN SECTION GS-body paragon as below. Its unique
mathematical pyramid (here coined »Cheops Rectangle») bd=h² geometry views a corresponding
IDEAL Petrie Cheops Rectangle Petrie¦CR from Petrie’s measures on Cheops Pyramid,
the Petrie¦CP.
Differences outside illustration —
see illustration in ScaleDiff
— In this
scale, even with the pyramid form (height or base) covering a total computer screen
of 12 inches (0.3M) differences between Petrie¦CP and Petrie¦CR or even rJ¦CR
will not appear to our optical eye due to the (very) tight small physical
differences at the actual building.
GSParagonArithmetics: GS body Paragon
The inner pyramid design in this
illustration has been as thoroughly as possible adopted to the measuring values
from The
1883 Flinders Petrie measurements.
The lower shaft or well (next to x)
has not been drawn out here as Petrie [”so evidently utilitarian”, PetrieCH7.46e] never made
measures, while other authors (HelpILL) have made
slight different approaches: no related data on this part is yet known except
for the end openings. The marked red point is where we onset a pair of
compasses to envelope the rectangle [bd=h²] defining the Golden Section
Relation number R = [√5 — 1]/2 = 0.618033988, with (many) equivalents.
Deductions to
all mathematical expressions and connections used here of our gauging GS-body are (also) shown in more detail in
(Swedish edition from Nov2017) GS-GEOMETRY with all the basic MATHEMATICAL
CONNECTIONS.
GSTarCO: The7
The Golden Section paragon geometrical
quantities — exactly DEFINING THE 7
FOUNDATIONAL POINTS
THE FOUNDATION LINE CONSTRUCT
The CONSTRUCT FOUNDATION LINE
THE 7 FOUNDATION POINTS — K L M G H B A
The 7 GS-body xyCoordinate points [TarCO] ¦ The AG-condition ¦ ConENTER ¦ Petries19th ¦ The dSIDE ¦ ConPENT ¦ The P-point ¦ The B-point
¦
Based on Table of results
OUR exercising MISSION:
Our exercising
mission is simple:
— Use the given
GS-body — as
illustrated in the Table above — to extract the most simple and
direct VISUALLY seemingly FIT with the given (Petrie) measured edifice.
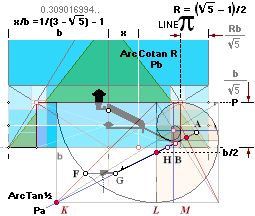
The xy-origo is related to the
pyramid’s north side base point, rightmost in this illustration.
+xy rightUp, —xy leftDown.
Below is the
account for all the readouts of all the xy¦P-coordinates for all the Table
parts K L M + G H B on the central ArcTan½ sloping line. It ends on the point
A-intersection at the pyramid ideal casing mantle side by the GS-body angle C°
= ArcCot √R.
— The aim of
this ArcTan½ line specific exercise is to ASSERT and CERTIFY any person that the given
KLMGHB-points define one and the same, and only so, ArcTan½-slope ON the A-intersecting
point, giving one and the same, and only so, end point intersecting xy-values:
— We must be
VERY sure on this point, so no hazard or adventure will pop up later. Because
this IS the foundation of the whole quantitative concept, as will be seen.
— The Table shows the
results as a perfect certification on all the named points:
The ArcTan½ line
point coordinates: ArcTan½
Line ¦ GSTarCO
We relate the
Tabled-used GS-geometrical KLMGHB-xy coordinate points here from the given GS-paragon’s visual fit (some acquaintance is needed to familiarize the
connecting GS-geometrical details: without further, we assume full insight):
Kx —b(1 + R^3 + R/√5) = —b(1 + b4 + PiLINEx)
Ky b(1//√5 — 1) = P — b
Lx —b(R/√5 + R^3) = —(PiLINEx
+ b4)
Ly b(1//√5 — 1/2) = P — b/2
Mx —b(R/√5 — 0.4R^3) = —(PiLINEx
— 0.4b5)
My b(1/√5 — R^3 — 0.8R^4)
= P — (b4 + 2 · 0.4b5)
CLARIFYING xy¦M:
— The often
useful hABb triangular formula can be
utilized to find the form of xy¦M:
— There is
another perpendicular ArcTan½-line with the same internal (in a lower
GS-fraction) GS-property as our main ArcTan½-line. These two intersect in the
point Pb where the xM-part is calculated directly as illustrated:
b5REF: GSTarCO
The triangle
ArcTan½-90°-ArcCot½ gives for two consecutive calculations from hypotenuse (b)
to longest right-angled side (b/√1.25)/√1.25
= b·0.8;
— As always
sin²+cos²=1, the corresponding end shortest side will count by b·0.2
— for the
ArcTan½-triangle only.
PiLINEx —
0.4·b5, see illustration above through the hABBb connection.
— Given Mx,
also the vertical My-part becomes directly given as twice the Mx-part through
ArcTan½:
2 · 0.4b5 =
0.8b5 = My-part.

The xy-origo is related to the
pyramid’s north side base point, rightmost in this illustration.
+xy rightUp, —xy leftDown.
Gx —b[1 + R/√5 + R^3 — 2(1 — 1/√2)] = —(PiLINEx +b4 — 2|Gy|) ....... =
-4221.8156658449’’¦4221.82
PETRIExP = xG + 10R
.................. = 4227.9960057324’’ ¦
4228.00
Gy —b(1/√2 — 1/√5) = —(b/√2 — P)
.............................................................. = -1184.0412529906’’¦1184.04
PETRIEyP = yG — nValue .............. = 1181.2240228242’’ ¦ 1181.22 NOMINAL
PETRIEyP = yG — nValue
.............. = 1181.2313270982’’ ¦
1181.23 piVERSION
CLARIFYING xy¦G:
— The GS-body
is explicitly clear on this point:
— The GS
b-diagonal intersects the b-square’s partial GS-circle in the F-point through
the inverted 2-root:
y-part = b — b/√2.
Related to the the upper we get a simple total
My = —(1/√2 — P).
x-part = twice the y-part through
our ArcTan½ line: x/y=2. Mx in
total then: b—2My+b4+PiLINEx, or
minus(PiLINEx
+b4 — 2|Gy|).
Hx = Ax ............ Hx can only be calculated with respect to a given ArcTan½
endpoint.
Hy 0 ................. H intersects the Petrie pavement measuring
ground reference line.
Bx see PHASE 2.
By see PHASE 2.
Ax same x-intersecting result from all
four KLMG-points
Ay same y-intersecting result from all
four KLMG-points
Phase1RESULT: PHASE 1
SUMMING RESULT
— The Construct Foundation Line from Pyramid North:
All KLM GB share exactly the same ArcTan½ line with one and
the same end point
xyA -523.0566039073’’;665.3382779782’’
on the pyramid ArcTan R-side.
— These basic
reference points define the further inner design points of the building.
Rough Overviewing RESULT
— The G-point
and the A-point explain the absolute basic quantitative inner Cheops Pyramid
GS-design;
— THE
FOUNDATION LINE with respect to the crucial G-point as illustrated below in a
compressed overview. This illustrative approach is greatly exaggerated from the
actual view by purpose of enhancing and elucidating the else-way tight
differences between the several slight differing angles and values. We will
relate these in detail.
SCHEMATIC OVERVIEW
— Cheops Pyramid inner design:
See also fully related the
corresponding/equally Petrie calculated angular values in TP27.
See also The Petrie D point.
(PG→yBlow)° ArcTan½ ........ rJCR¦b16
(pG→yB)° 26°
1’ 3’’ ........ rJCR¦b16,
PetrieCR¦b58
(pG→B’)° 26° 12’ 51’’ .... PetrieCP
(D→B’)° 26° 3’ 59’’ ...... PetrieCP
(D→pG)° 26° 12’ 34’’ .... PetrieCP
————————————————
Because the Petrie measures NOW are PRACTICALLY defined by the two pyramid
agents rJCR¦b16 and the ideal corresponding Cheops Pyramid as the Cheops
Rectangle PetrieCR¦b58 — their difference is discernible — it makes no longer a difference if we
calculate directly from the Petrie given measures — including his given
tolerances — OR if we calculate directly from the actual pyramid agents and
their exact zero tolerance: all values become collected anyway within the the
Petrie given tolerances.
ROOF18: Proving the 19th
Further ahead
A SECOND
A-POINT DECISIVE QUANTITY RESULTS FROM THE FIRST A-POINT RESULT
The Petrie 19th course — Petries19th — floor
construction level
yA + n = Petrie’s18th
roof. Case Closed.
There is no any
the slightest doubt that the 1883 Flinders Petrie working group measured Cheops
Pyramid has definite quantitative constructive properties connected to the rJCIRCLE and its ideal Cheops Rectangle geometrical
(nuclear) mathematical
physics.
— IF we would
be the ones who should build a monument for a future humanity to find proof on
fundamental nature harmonic nuclear grounds, this would definitely be it.
With a Petrie
given (broad)) tolerance ± 0.1’’ (± 2.54 mM) on the 19th course floor height
over the pavement, the rJCIRCLE calculated quantities 668.15’’ or 668.16’’,
depending on convenience, can be apprehended as a direct constructive hit. The
difference from the nominal 668.2 is only 0.05 or 0.04. That is only 1 mM —
still after (many) thousands of years.
See first, unless already
acquainted,
Why there is only one unique
parallel relationship rJCR¦PetrieCR.
Then the actual connecting
explaining in
How the A-point Defines THE DECISIVE
Petrie 19th COURSE floor
level by the established 7 points AG
relations (TarCO)
Then the additional (very)
interesting
How Petrie Reckoned the Cheops Pyramid
Entrance.
— The B-point
explains the inner design ”final count down” with respect to the so called
Great Gallery and its dimensional and angular properties.
— Point B
positions the point where — by ideal construction and a corresponding (later)
measure — the downward and the upward tunnels meet, and how the construct point
matches the Petrie measuring values.
As instructed
by Petrie’s given measuring tolerances, NO QUANTITATIVE DEVIATIONS will be
accepted here. This expedition is solely dedicated a fundamentally tight an
maximum exact examination of the agreements, coherences and concordances
between Petrie’s values and those emanating from the rJCIRCLE complex: The Cheops Rectangle’s ideal Golden Section paragon math. Our two EXACT GeoMATHematical agents rJCR¦b16 and its ideal
spouse Cheops Rectangle PetrieCR¦b58 determine the resulting quantities: The
one and only unique bh=h² Cheops Rectangle pyramid construct.
SHORT OVERVIEW
Phase1RESULTpoint ¦ G
Some
complementary rJCR¦b16 calculated results are shown in the point G region
below.
— See the
rJCR¦MEAN 45.93’’ math in DescendingPassageLowHigh.
Two different GS-body
projections form a mean construction line between two Petrie given values.
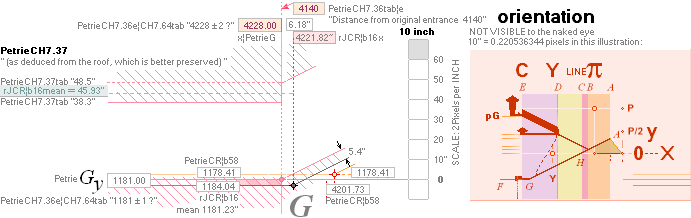
The plain text values are:
PetrieCP¦b 4534.40’’±
0.25
PetrieCP¦x ”4228 ± 2 ?”, PetrieCH7.36e¦64tab
PetrieCP¦y ”1181 ± 1 ?”, PetrieCH7.36e¦64tab
PetrieCP¦height ”48.5”, PetrieCH7.37e, [”as deduced from the
roof, which is better preserved”]
PetrieCP¦height ”38.3”, PetrieCH7.37e, [ ].
—————————————————————————————
rJCR¦b16 4555.88 ....... the actual exact rJCIRCLE Cheops Rectangle pyramid half base
rJCR¦b58 4534.20 ....... rounded to two decimals from b =
58R√16000 = 4534.1965576 ¦ featuring an ideal PetrieCR
The GS-quantities
here are taken from the xyG column in Phase1TABLE OF RESULTS.
More precise
and detailed G region quantity representations are given in Main Construct.
THE AG-CONDITION
WHY
THERE IS ONLY ONE UNIQUE PARALLEL relationship
BETWEEN
THE TWO IDEAL GEOMETRICAL CHEOPS PYRAMID AGENTS
The values
below comes from The Result Table.
— Because the
two geometrically ideal exact but differently sized pyramids rJCR¦b16 and the ideal PetrieCR¦b58 have only one
unique mutual projective distance through parallel straight lines, other coordinate
relations between the two will have other (unique) parallel relationships.
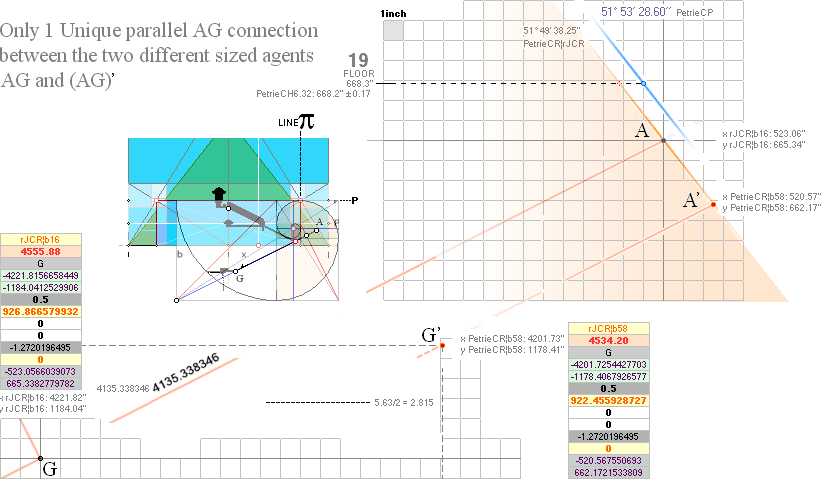
Prioritizing
the G-point determination from a relation based on the pyramid ideal (A) casing
flat surface, will establish a fixed and definite, non changeable relationship
between these two basic outlets — hence determining an entire constructive —
exact quantitative — layout of the whole building.
The vertical
(y) offset difference — yConOFFSET — between the two is
yConOFFSET = 4.4106512044’’; 
— See NatCHintro for the iconic details, unless already familiar.
MOST SIMPLY
CALCULATED AS ABOVE the yConOFFSET quantity is found
through the
ArcTan½ triangle, in absolute values:
(yA — yA’) +
(xA — xA’)/2 = 4.4106512044’’:
Because this
offset is related to BOTH pyramid agents ON THE SAME LEVEL
— the main
rJCR¦b16=4555.88’’ and the actual Cheops Pyramid’s corresponding physically
ideal Cheops Rectangle PetrieCR¦b58=4534.20, as within the PetrieCP¦b=4534.40 ±
0.25 tolerance
— its RELATION
is also conserved as such:
— a TRUE
Pyramid Constructor Base Line is established.
The offset value can be — and is — used in
defining possible exact connections to the Petrie measured Cheops Pyramid
values — or not at all.
For the G-point
determination coordinates, see TarCO from PHASE 1.
ConENTER: 18Jan2020 — PHASE1 — Confirming 19th ¦ The Petrie Point ¦ Pangle ¦ Hangle ¦
The GS-body Paragon Pyramid
CONSTRUCTION Entrance Point (A)
After having
noted THE FOUNDATION LINE CONSTRUCT — a complete match from Petrie’s
measurements of the Cheops Pyramid along with an explaining geometry — it will
HERE be more convenient to take this lead:
— EXPLAINING
THE CONSTRUCTION. Along with presenting the quantitative matches.
— And of
course: yearning for any opportunity to meet with a general failure.
CARING TO TO PRESERVE THE
CONSTRUCTION LINES
some offset to the actual physical
floor must be granted.
Taking the basic Cheops
Rectangle unique bd=h² Pyramid coordinates from the GS-body with our
two agents
rJCR¦b16 and PetrieCR¦b58
we arrive at the following basic
picture:
ENTER: MainConstruct 
Enter
665.34 + 2.817 = 668.157 ~ 668.16’’:
Petrie’s 19th course floor ”668.2 ± 0.1”: ............ clearly approved ........... the
exact original
665.3382779782 + 2.8172301665 =
668.1555081446 = yA + nVALUE¦norm
665.34 + 2.810 = 668.150 ~ 668.15’’:
Petrie’s 19th course floor ”668.2 ± 0.1”: ............ clearly approved ........... the
pi-number adopted
version
665.3382779782 + 2.8099258924 =
668.1482038706 = yA + nVALUE¦piForm
— Both these apply well within the
Petrie given tolerances: 668.20’’ ± 0,10.
Pushing the far ends more close
along the PARALLEL CONSTRUCTION LINES, see The AG- CONDITION,
magnifies the narrow angles —
creating an exaggerated illustrative effect.
See also detailed math in Hangle [The H°Angle]
and Pangle [The P°Angle].
The GS-paragon
Pyramid Entrance: ENTER
See also yConBoffset and [18thRoof] PROVING THE PETRIE 19th Floor — 18th Roof — ARITHMETICS. The figures
here — 1.4086¦2.817¦3.1497.. — reflect the exact PetrieCR¦b58 and
rJCR¦b16-calculated original through the points AA’ GG’. In examining these
values, the number of pi = 3.1415926.. has been adopted as a slightly more
favourable — yet close — value for the ease of reference. The difference
between them is anyway insignificant with respect to the Petrie given
tolerances. By the same standard of our convenience, the quantity 10R has been
adopted — as it is practically the actual Petrie horizontal offset relative the
rJ G-point. It is here assumed, that these convenient figures also would have
attracted the original constructors in giving us, here in our aftermath, a not
to difficult way of »cutting to the chase».
Note that Petrie [See full Quote in PetrieCH6.24] measured the
[idea of the original] casing pyramid from the remaining staircase masonry slope
values, and a few of the casing stones at the base.
— In this illustration on the scale
of single inches, the differences are factual and directly inspectable.
— The CASING blue line represents
the Petrie staircase measured slope 51° 53’ 28.6’’ while the orange part
belongs to the ideal GS-body
Cheops Rectangle ArcTan 1/√R-value 51° 49’
38.25’’.
SpotLimit: ENTER
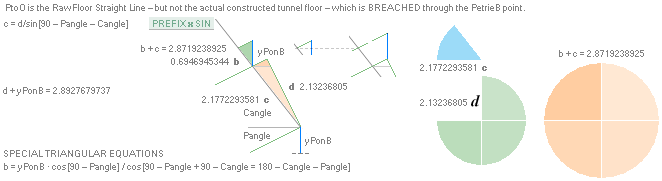
yPonB = 18·TanPangle — 2·yBlimit = 0.7603999237’’.
yPonB directly appears from the Petrie
B point definition as an overlayed extra vertical offset factor »y UPON b».
yPonB connects the actual physical
floor, its possible sight line, with the pyramid’s outermost visible material —
as seen from inside the narrow 105 M long dark descending tunnel ![]() .
.
— With its quantity we can calculate
the exact optical window through the descending tunnel for Petrie to spot the
casing region from where the 19th floor properties were derived.
See further full details from ENTER, The F Angle and Proving The 19th Floor
Arithmetics.
GSbasic: ConEnter
Taking The Basic.
This presentation shows
•
how the parts of the building are tied together by exact quantities
between an original rJCR¦b16 and PetrieCR¦b58 casing and the
GS-body’s advised
parts and their constructive layouts.
The Topics below link to actual sections.
Confirming The 19th ¦ The Petrie Point — overview
¦ Main Construct ¦ Floor Construction Angle ¦ The Petrie Point ¦ Petrie Ref. H-angle
¦ H-ANGLE CALCULATION ¦ Confirming The 19th ¦ ResultsBasic ¦
— See full quote of Petrie’s 19th
floor in Petrie’s19th.
•
a confirmation of the whole inner design of the Cheops Pyramid through
exact numerical quantitative values with zero tolerance connecting to
the GS-paragon body —
depending entirely 100% on Petrie’s onset on the entrance complex. See from ENTER.
Specific rJCR¦b16 A-G values are
taken here from The
Result Table — both pyramid agents A-G values are as calculated from
the CalCard:
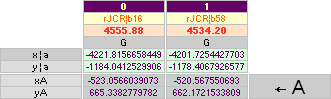
The Result Table text section
details how the coordinates were calculated from the GS-body paragon
geometry.
The Petrie
Point: ThePePo
OVERVIEW
The Petrie P point
The bottom GG’ points from the two exact GS-body agents rJCR¦b16 and PetrieCR¦b58 form a
2n BAND MARGIN
with nominal height 5.63’’.
— In the middle
of the GG’ 5.63 height stripe we find the corresponding Petrie point P value
slightly (+0.225’’) positioned over the GG’- midpoint.
With the
PetrieCH7.36e given height
1181’’ and Petrie’s given tolerance ”± 1?”, we
see that the difference 0.225’’ is negligible
— like »a
perfect hit».
We can’t prove it is NOT. And we can’t
prove it IS — except the fact that it is positioned within ”it is”: approved
with tolerance. So »it is».
— The
constructive ideal midpoint in P’ (P prim) is calculated from the rJCR master G
-point through an end edificial condition:
MainConstruct:
COMPRESSED VIEW — ENTER
¦ ConENTER ¦ EnterGSPyramid ¦ ThePetriePoint ¦ Pangle ¦ Hangle
— G’ values [GENERAL PRIM-] use the PetrieCR¦b58 = 4534.20’’ agent and the
G-values use the rJCR¦b16 = 4555.88’’ agent. See CalCARDmethod.
Given the PetrieCH7.36e¦64tab
Petrie xy P measured values 1181; 4228 and
their relatively hight xy tolerances,
as quoted ±1?;±2?, and
our two above named pyramid agents calculated yP’ value
1184.04 —
([1184.04 — 1178.41 = 5.63]/2 = 2.815 = n) = 1181.225’’ or more
precisely without decimal cuts
1184.0412529906 — 5.6344603329/2 =
yG — n =
1181.2240228242 with a nominal Petrie difference 0.2240228242, 2 decimal
rounded as 0.224’’
PetrieyP = 1181.0 ± 1 ?
showing only a
nominal Petrie measured vertical difference of 0.22’’
there is no scientific way for us to
exclude a compelling fact that we are looking at a highly intended construct
PLAN. The more so in observing the close and convenient horizontal PP’
difference between our calculated 2 decimal rounded 4221.82’’ and Petrie’s
nominal 4228’’ as exactly 61.8’’ = 10R:
xG + 10R = 4227.9960057324
PetriexP = 4228.0 ± 2?
Compare ROSSI2002: As we know it [with some
reservations], the 2 500 BC Egyptians hardly even knew anything at all about 2R
= 5^½ — 1; R = 0.618033988.
— And MiUNIT: it had to be in INCHES too. So:
Classic Modern Academic ancient Egypt scholars seem not to have much mandate
here: A past GeoATLANTIS is calling attention.
PetrieCP¦xP ................. ”4228 ± 2 ?”, PetrieCH7.36e¦64tab
PetrieCP¦yP.................. ”1181 ± 1 ?”, PetrieCH7.36e¦64tab
SECURING THE
BASIC GS-PARAGON
CONSTRUCTION LINE AG from hazard — burying it in the bulk masonry, yet preserving
its geometrical foundation — demands some definite offset to an actual corridor
floor (the Petrie named Descending Passage tunnel from the pyramid north casing
side entrance A).
— A maximum
G-point right angled GP’ offset can be calculated BY USING ONLY NATURAL
(mathematical geometrical [transcendental — any SAFELY KNOWN available, easy to
deduce]) CONSTANTS by intersecting the GG’ mid-line with an AG-normal (|_) from
point G as follows:
The P°Angle: MainConstruct ¦
— With a more
direct decimal calculation: GG’ = 2n = 5.6344603329; n = 2.8172301665
(GG’/2 =
2.8172301665) × √1.25 = 3.1497590802’’ ¦ (pi = 3.1415926)/√1.25 =
2,809925892 = MODIFIEDnValuePiVersion;
n = nValue = pi/√1.25 = 2.8099258924’’ ¦
pi [π] = 3.1415926;
Pangle via piVERSION for nValue
........ 2.8099258924: ........... 26° 31’ 17.48 60 86’’;
Difference to Petrie’s PangleLow 26° 31’ 18’’: ........................................ 0.51 31 40’’.
Pangle via GG´/2 for nValue
................ 2.8172301665:
........... 26° 31’ 17.07 87 56’’;
Difference to Petrie’s PangleLow 26°
31’ 18’’: ........................................ 0.92 12 44’’.
WITH SOME ASSISTED CERTIFIED HELP
FROM PETRIE’S GIVEN QUESTION
MARK;
— We adopt IN TESTING THE CHEOPS
PYRAMID SUGGESTED ADVANCED HIGH TECH PLANNING
the higher [possibly rounded as 18’’] as The Constructive the rJCR¦PetrieCR
calculated P° angular value.
— But we will frequenly refere borth
candidates to show that their difference plays no significant role on the
overall constructive picture.
PetrieCH7.36e describes the whole tunnel’s
mean angular value — see also in InvEX1:
” 36. [p. 58] The azimuth and
straightness of the passage were carefully measured. The azimuth down the built
part was taken by reference to the triangulation, which in its turn was fixed
by six observations of Polaris at elongation, from a favourable station (G).
The azimuth to the bottom of the rock-cut passage was observed independently,
by five observations of Polaris at elongation. The observations of the
straightness throughout gives a check by combining these two methods, and they
are thus found to agree within 19”, or
just the sum of their probable errors, equal to only
.09 inch lineally on the azimuth of the built part.
The results are:
Azimuth Altitude
Mean axis of whole length. – 3’ 44” ± 10” 26° 31’ 23” ± 5” ?
”.
FloorConstructionAngle:
The P°Angle
Temptingly
close to the conveniently inviting transcendental pi number 3.1415926, if we
»buckle up and pine in» to that attempt as Presumed Constructors for aftermath
students, we arrive at the destination
The Pangle
— The
Construction Angle P° = AGP’
rJCR¦b16GAslope = 4135.338346’’ = (xG—xA)(1.25)^½ = [4221.8156658449’’ — 523.0566039073’’ =
3698.7590619376’’]√1.25
P° = ArcTan½ –
ArcTan(π/4135.338346’’) = 26° 31’ 17.48’’
PetrieCP¦xP ”4228 ± 2 ?”, PetrieCH7.36e¦64tab
PetrieCP¦yP ”1181 ± 1 ?”, PetrieCH7.36e¦64tab
See also this Petrie angle in Investigating Example 1.
See also how the Pyramid casing
entrance point A connects Petrie’s observations in EnterGSPyramid.
The Petrie Point: ForCA
10R — The Petrie P point (P)
— Obviously on
»a float of Natural Constants», we might as well »throw in» an extra additional
10R (MiUNIT/10) »to get some
distance to the Petrie xP-point» and its x-value:
rJ-DEFINITION OF
THE PETRIE P POINT
rJ-DEFINITION OF THE PETRIE Subterranean P POINT
In
PetrieCH7.36e¦64tab
”4228 ± 2?”
compared to the
rJCR¦b16 xG value
4221.82’’ ±
0.00 , we have
xP — xG =
4228.0 — 4221.82 = 6.18’’ = 10R.
(”And the hits
just keep coming”).
Exactly.
— That would
be: a PLAN.
SUMMING UP
The Flinders
Petrie working group (1881-1883) obviously made excellent measures.
The Breaking point
(H, pyramid
base cuts the ground level)
to the Casing Construct Original
Entrance point (A)
The Central
Aspect
— How about the
(ForCA) illustrated
BREAKING point at H, directing the floor to the construct original casing
entering point A into the actual GS-body paragon, the Petrie named descending
tunnel from the casing surface?
See HOW
PETRIE RECKONED THE ENTRANCE for the
math-part — and EnterGSPyramid.
— Petrie’s
measuring arrangements (StationMark) explain the details in quote PetrieCH6.31.
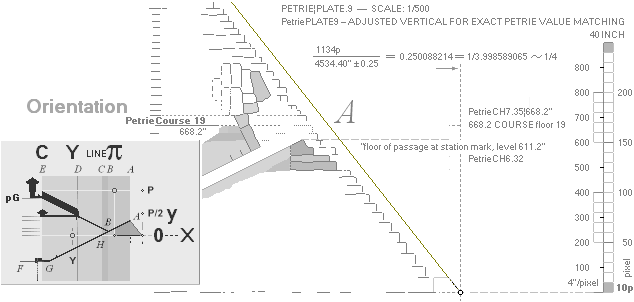
See also: DRAWING SPECIFICATIONS in The
Entrance.
The H°Angle: The P°Angle ¦ ThePePo ¦ Main Construct
The H° angle —
The Hangle
— PetrieCH6.32e: 26° 29’ ± 1’:
”(4) entrance passage angle at mouth 26° 29’ ± 1’; ”
H-ANGLE
CALCULATION: Hangle ¦ Pangle
As we know:
— There is only
one referencing
Cheops Pyramid
Inner Design Descending Entrance Tunnel CHEOPS RECTANGLE
region to which
we can relate a Petrie corresponding angular value of 26° 29’:
— Where
the IDEAL CHEOPS RECTAngle Pyramid base
intersects the ground zero level:
— The H-point
connecting the fundamental (Enter)casing A
point.
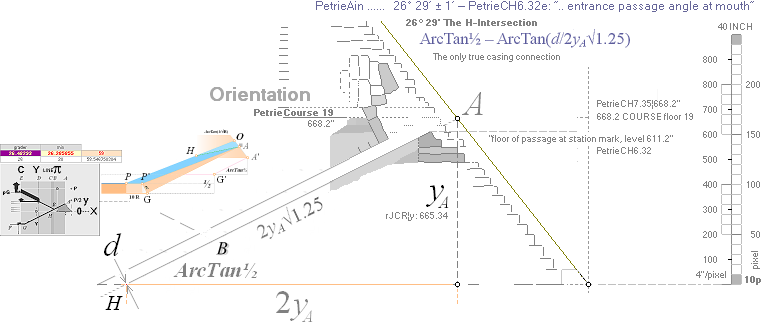
See Finding d.
SOLUTION (with
an investigating lead as Testing Constructors):
— We simply and
undramatically BORROW the calculated dValue from the
primary defined subterranean part (Petrie P ¦ Enter) and HANG it
as a right angle distance onto the given ArcTan½ foundation:
— This will NOT
result in any construction part. It is ONLY a METHOD for us — the only SIMPLE
deductive one we know of here — to acquire a 29° 21’ angular value from the
given Most Simple premises. Then we can use this with parallel constructive
levels to settle a final actual physical construct (whatever seems suitable for
the purpose).
Simply as
illustrated:
H° angle =
Hangle = ArcTan½ — ArcTan(d/2yA√1.25) =
Hangle = 26° 28’ 58.54 67 58’’
— PetrieCH6.32e: 26° 29’ ± 1’:
”(4) entrance passage angle at mouth 26° 29’ ± 1’; ”
— Approved.
APPLICATION — nearest:
— See yConB: how the rJCIRCLE complex determines the decisive Petrie B point.
Confirming19th: FINDING THE d-SIDE ¦ HangleCalc ¦
Finding d (2.13’’) — with a
confirmation of Petrie’s 19th floor
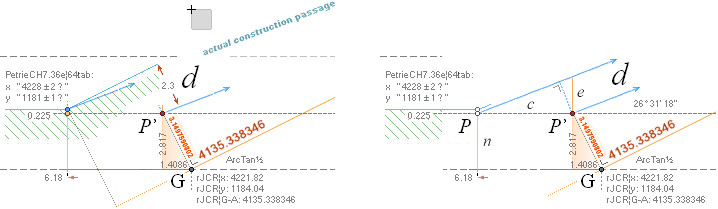
Selecting a lower P’G-value than the
default — we adopt the pi-value 3.1415.. instead of the slightly longer default
3.1497.. — means we change the basic conditions: However, preserving the 10R =
c as a constant separating distance, we adopt the other parts to it and
finalizes by calculating d over the former (minimum) derived angle (P° = 26° 31’ 18’’ with the use of pi for P’G).
The end results will show us anyway how this works — if at all. [It works].
RESULTING
VALUES:
n1 = π/√1.25
;
n0 = (yb16 – yb58)/2
c = (10R=6.18) – n1¦0/2 ; = 4.7753769413’’
e = c·TanP° ; = 2.3831554097’’
PREFIXxSIN [PREFIXxSIN] : d/e=sinP°; (d/c=cosP°;
d=e·sinP°=c·cosP°);
d = e·sinP° ; = 2.1323680500’’
H° = ArcTan½ – ArcTan(d/L) ; = 26°
28’ 58.5467583038’’
L = AH = 2y(A)√1.25
;
ResultsBasic: Confirming19th ¦
RESULTS:
26° 28’ 58.55’’ .................. H angle = 26.4829296551°
PetrieCH6.32: ”(4)
entrance passage angle at mouth 26° 29' ± 1'; ”
——————————————————————
Petrie’s Cheops Pyramid Course Floor
No19 found
— defined and confirmed by rJCR¦b16 n+yA:
— Entrance (A)
connects the 19th floor with subterranean (GG’) via
nValue +
yA¦rJCR¦b16¦665.34’’ = 668.2’’:
d = 2.13’’:
P’G n c e d H°
3.1497590802 2.8172301665 4.7717248043 2.381321038 2.1307288152 26° 28’
58.77’’
3.1415926536 2.8099258924 4.7753769413 2.3831554097 2.13236805 26° 28’
58.55’’
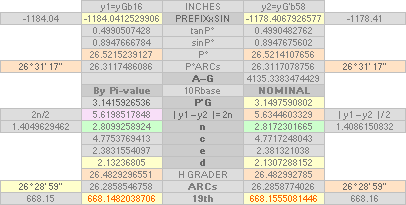
Exact calculated values from the Golden Section paragon body NatCH through the rJCIRCLE¦b16 and
PetrieCR¦b58 Cheops Pyramid Agents.
Compiled and presented 18Jan2020 for
UNIVERSE HISTORY — no rights reserved: knowledge — universal energy — is for
free.
THE H-ANGLE rounded 26° 28’ 59’’ ~ 26° 29’
— based on the d-side (also defining the P-angle minimum 26° 31’ 18’’)
— is just only practically
1 arc second (1’’) from Petrie’s 26° 29’ 0.00’’.
— With Petrie’s
stated ± 1 arc minute tolerance our arc second difference has no meaning here.
See also the Rossi2012 reference:
— The ancient
Egyptians (hardly, as we see it) knew The Math — as we know it.
We are obviously dealing with a
sophisticated and advanced mathematical and physical plan for the whole
edifice.
See also
HOW PETRIE RECKONED THE Pyramid
ENTRANCE GEOMETRY:
Petrie’s
description follows in partial quotes.
All the
following numbers are given from the Petrie quote in PetrieCH6¦31-32.
— Here we just
relate the reckoning details — the figure below.
PETRIE MEASURES THE CHEOPS PYRAMID ENTRANCE — see
following citations:
Related Trigonometric Specification: PREFIXxSIN is
used in Universe History, unless otherwise mentioned:
![]()
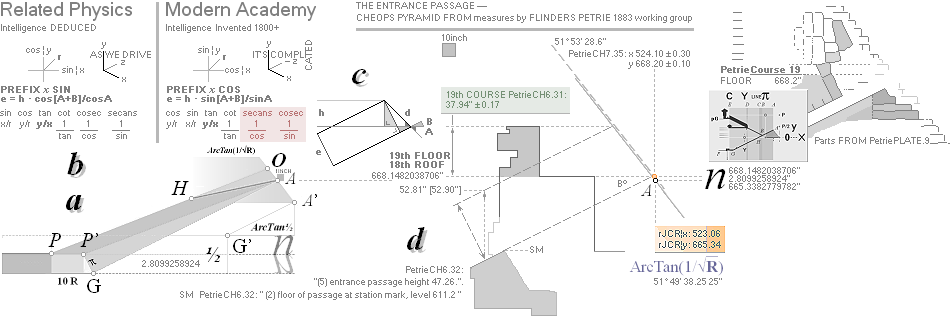
— What means ”Prefix
X sin” on my conventional scientific sin cos tan calculator? Just
shift/think the labels SIN COS for COS SIN. Same buttons. Nothing else.
— Why the SINE prefix? Most animals are
broad sighted —————— : The Horizon (x-axis) is the most viewed fundamental. Not
the (co-) vertical.
c: CALCULATING h
FROM e OR e FROM h ON GIVEN ANGLES AB — Deduction: Familiar with trigonometry (we always use
the simple, straight and direct easy to remember PREFIXxSIN in Universe
History) we have h/d=cosA giving d=h/cosA. Adding the two angles AB together
gives
e/d=cos(A+B) with e = d · cos(A+B).
The answer: e = h · cos(A+B)/cosA ¦ h = e · cosA / cos[A+B].
b: EXPLAINING THE
TWO DIFFERENT TRIGONOMETRIC PREFIXES.
a: The
Cheops Pyramid Complex rJCIRCLE Main Construct — origin of
the nValue.
d: Actual
Site: The Cheops Pyramid Entrance Complex, as described in PetrieCH6.32. TP1 ¦ TVTuS ¦ SumParts ¦ Petrie19thProof.
Petrie’s data along with
PetrieCH7.35 ””:
” Having, then, fixed the original
position of the doorway of the Pyramid, we may state that it was at
668.2 ± .1 above the
pavement of the Pyramid;”,
PetrieCH7.35.;
” mean doorway height ¦ by measuring
courses ¦ 37.94 ± .17”
”The data for calculating the result
are
(1) levels of the 19th course by
entrance 668.30 and 705.97;
(2) floor of passage at station
mark, level 611.2
(3) which is inside the edge of the
base of the casing horizontally, 638.4;
(4) entrance passage angle at mouth 26° 29' ± 1';
(5) entrance passage height 47.26.
” PetrieCH6.32.
— Petrie gives no actual written formula.
But we can check and cross-check the values by using the above deduced
connections:
PetrieConPent:
PetrieCH6.32 Row32 Quote ¦
Petrie
describes the 19th course thickness with a specified tolerance at most
with
h = 37.94’’ ± 0.17 — with (Hih38.11,
Low37.77) an end result for the floor normal e-factor above as
e = 47.26’’ (~47.3); PetrieCH6.32 Row56 ”(5) entrance passage height 47.26” gives the angles
A = 51° 53’
20’’ ± 1’ ............ =
51.88888...° = 51 + 1/1.125 °: the PetrieCH6.32 Casing surface ”the face of the casing”;
B = 26° 29’ ±
1’ .................. =26.48333.... ° = 26 + 48/100 + 1/300 ° ; In
PREFIXxSIN:
How Petrie took the reckoning grasp:
e = 37.94’’ · cos[51+1/1.125 + 26 +48/100 = 78.36888..
]/cos[51+1/1.125] = 47.229552845’’.
— Taking these angles for given, the
e-answer must use a lowest h = 37.964’’ to get
a least rounded Petrie mentioned
e = 47.26’’ (47.25999..).
— However as
the h-value can be as high as 37.94+0.17= 38.11, a type value of
h = 37.97 does
the job for an e = 47.26 (Petrie gives no exact input parameters; as we see,
there are ”many to chose on”).
— NOTE: Petrie
explicitly names the e-part ”entrance passage height 47.26”, NOT a Vertical Height — which, through
the simplified ArcTan½ angle should read
e · √1.25
= 52.84’’ — or 52.80068666’’ with PREFIXxSIN e(Vert) = e/sin(B=26° 29’).
But see these
comparing results:
Petrie’s values with Petrie given
tolerances matches the ideal corresponding
Golden Section paragon body Cheops
Rectangle calculated quantities:

With all the
differences contained inside the Petrie given tolerances
(hPetrieCP =
37.94’’ ± 0.17)
(ePetrieCP ;
47.26’’ ¦ 47.30’’ ; PetrieCH7.32, no specified tolerance:
”(5) entrance
passage height 47.26”.)
it makes no
change in the overall resulting picture if we select the Petrie given data or
take the ideal received quantities from the rJCIRCLE complex:
with A =
Petrie’s measured 51° 53’ 20’’
From e =
42.26’’:
B = ArcTan½ 26°
31 23’’ 26° 29’
h = 37.9529038928 37.9585978760 37.9640039644
PetrieLowestApproved h: 37.77’’
PetrieNominal 37.94’’
PetrieHighestApproved h: 38.11’’
— All apply.:
with A = Golden
Section Cheops Rectangle ideal in PREFIXxSIN ArcSinR = 51° 49’ 38.25 25 43’’
From e =
42.26’’:
B = ArcTan½ 26°
31 23’’ 26° 29’
h = 37.9292286343 37.9349502165 37.9403824145
PetrieLowestApproved h: 37.77’’
PetrieNominal 37.94’’
PetrieHighestApproved h: 38.11’’:
37.95 row
2 RightLeft PETRIE
37.96 row
3 RightLeft PETRIE
37.96 row
4 RightLeft PETRIE
37.93 row
2 RightRight rJ ¦ NatCH
37.93 row
3 RightRight rJ NatCH
37.94 row
4 RightRight rJ NatCH
In fact, as we
see, the latter part adopts more close to the Petrie referred nominal values
(h=37.94).
— What does
that result mean or prove?
— IllustrationPARTd emphasizes something like:
— GIVEN THE
19th COURSE FLOOR LEVEL (y19th = 668.2’’ ± 0.1) with its HEIGHT or thickness (Petrie’s
averaged mean 37.94 ± 0.17) PRACTICALLY LITTLE OR NOTHING changes with a SMALL
difference between an ideal casing angle A = ArcTan √1/R or the Petrie
given slightly larger A = 51° 53’ 20’’.
In other words:
— The Petrie
given data will NOT have any priority over the rJCIRCLE calculated quantities:
y19th h
PetrieCP 668.2
± 0.1 37.94 ± 0.17
PetrieCR 668.1482038706 37.9403824145 with
rJCR
See Enter The
Petrie19thProof
RESULT:
In other words,
as no notified detail interferes with the conclusion:
most exclusively and gallantly
quantitatively as this part as shown
be comprehended
as a DEFINITION of the (very gallantly performed) Petrie measuring conditions.
Petrie comes to the point ”entrance passage height 47.26” In Quote PetrieCH6.31 Row43.
QUOTING PETRIE
The Petrie ConPent illustrated math.
Petrie writes In Quote PetrieCH6.31 Row1 on TCA;
Petrie takes
arguments from other pyramids In Quote PetrieCH6.32 Row11.
— See in
explicit: Proving the 19th Course Arithmetics:
————————————————————
ENTER ¦ MainConstruct ¦ SummingParts ¦ ThePush
————————————————————
— The two
pyramid agents define the nValue subterranean 2n STRIPE in which
midpoint the Petrie vertical G-point ’’1181 ± 1?’’ becomes identified:
— Summing the n-value with the entrance ideal rJ-calculated A
point vertical height value 665.34’’, practically in a direct hit, identifies
Petrie’s defined 19th floor height above the pavement (668.20’’ ± 0.10). The rJ
values present the close 668.15’’ or 668.16’’ depending on choice of preference
(original n, or an adopted convenient pi-value for the hypotenuse side to the n
value triangle, whichever is legal). By this order, the bottom (G) an top (A)
pyramid inner design construct parameters unite and become certified.
Note that
Petrie is giving a more precise height value (668.20 ± 0.1) in PetrieCH7.35b¦36e¦64tab which allows the Petrie In Quote PetrieCH6.32 Row52 stated ”668.3” for the height of the
entrance point — same as the 19th
course floor level.
— We use the
Petrie tabled value 668.2’’ ± 0.1 to refer Petrie’s presented value on the
19th course floor as a nominal measure of The Petrie Measured Entrance Point.
The Gallery
point pG: The
B-point ¦ PHASE 1 — ORIENTATION
GalCalcOW — 2:  GCOW1
GCOW1
GALLERY CALCULATIONS OVERVIEW part 2
THE GALLERY-B-ENTRANCE-19th
COURSE CONNECTION
The illustration clarifies how the Golden Section paragon geometry
through the rJCR¦b16 agent differs
from the actual Petrie measured Cheops Pyramid physics. All differences between
these are now calculable and so provable, as it has shown.
— Withe The Contracted bOFFSET push [building
constants define the 19th course thickness by trigonometric/optic projection],
these two will share the same descending roof. See ThePush1. See also the main Cheops Pyramid
rJCIRCLE proof on THE
CONTRACTED CONSTRUCT.
Add1.84: yBPcon — TVTus
yAdd1.84 = xBPcon/2 = yBPcon
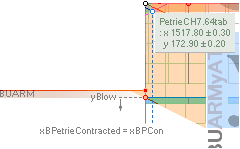
xBPetrieContracted = xB¦rJ — (xB¦rJ + 18 — bOFFSET) = bOFFSET — 18 = x;
yBPetrieContracted = x · Tan ArcTan½
= x /2 = 1.84 = yBPcon
With a final projecting bOFFSET PUSH (TP1) between the two pyramid agents
all acquired calculated constants
contribute to a single and final proving end result:
— The explaining connection between
the (Crucial—Row43) Petrie
original explained 19th course and its trigonometrically/optically projected
entrance (TCA):
cSideSUMMINGillustration: cSIDE = 52.889142448’’ ¦
yBPcon
————————————————————————
yATH ¦ yBlimit ¦ BUARM ¦ yBPcon ¦
For clarity. The cSIDE then
determines the thickness of the 19th course in a final optic/trigonometric
projection. See Proving
the 19th, also in copy below.
— As seen: It is fundamentally
impossible to deduce the construction PLAN — proving the quantities within the
Petrie given tolerances — WITHOUT familiarity with the rJCIRCLE complex , the two pyramid agents. They alone
are responsible for the entire quantitative edifice’s general mathematics.
As we know, see also ROSSI2002: The level of
mathematics in ancient Egypt had no such familiarity. So capitulating in front of
an overwhelmingly scientific fact, unless there is still more wonders to
discover: The building was set up a long time before, from an engineering
source we deeply and painfully are completely ignorant of, except for The Great Artifact.
— Our painful ignorance deepens
considerably in a broader sense with Petrie’s illuminating description of this
Casing-Tunneling projecting principle (TCA) as representative for OTHER PYRAMIDS TOO,
some located far from the most Northern Egypt Cairo-Gizeh location (PetrieCH6.2 In Quote Row12): same
principal/principle construct.
Possibly but completely unknown here: all of them. It is impossible to
avoid An Associate to South American pyramids too, with our ignorant level as
our guide. We need Explanations obviously outside the horizon of modern
academic ideation.
The D-form is the same type as in yConBoffset.
See also the summing parts in ThePUSH 1.
Summing the different parts together
defines the Petrie measured [37.94’’ ± 0.17] Cheops Pyramid 19th
masonry course height: The onset quantity of all the Petrie measured details of
the Pyramid’s inner design. See SumParts, Petrie19th proof, and ThePush1. PREFIXxSIN in TrigRef.
A: Cangle = ArcTan1/R^½. B: Pangle = 26° 31’ 18’’.
— The yATH and the BUARM — so — finalizes the calculation
expedition in also defining the Petrie measured 19th floor stone masonry course
thickness (37.94’’ ± 0.17) at the Pyramid’s North entrance at ENTER A.
LINE pi has no connection to the number pi.
2R = 5^½ — 1 = 0.618033988..
— See (TP1) the Petrie19th proof through the summing up (SumParts) of all the
named parts
c = yATH + yBlimit + BUARM + (bOFFSET — 18)/2
c = 43.37 + 4.11 +3.57 + 1.84 = 52.89’’; paralleling this value
gives the shortest tunnel normal
(52.89)/(1.25)^½ = 47.31’’ (=
47.3054871141)
A final trigonometric transformation
from entrance slope to horizontal masonry course through the casing slope —
Petrie’s specific 51° 53’ or our ideal Cheops Rectangle 51° 49’:
— both ways give practically the
same end result. They define the same Petrie 19th course thickness:
— As calculated (TheTrigonometricTransformation) with Petrie’s
values in PREFIXxSIN
37.9529038928’’ = cos(A=51°
53’’ 20’’) · 47.26/cos(A + [B = ArcTan½ = 26° 33’ 54.18 42 37’’])
37.9640590055’’ = cos(A=51°
53’’ 20’’) · 47.26/cos(A + [B = 26° 31’ 23’’])
37.9640039644’’ = cos(A=51°
53’’ 20’’) · 47.26/cos(A + [B = 26° 29’])
As calculated by the above
rJ-summing and the trigonometric transformation,
GENERAL GS-body: ¦ ArcTan
1/√R = Cangle = A =
51° 49’ 38.25’’ = ArcCot√R ¦ sinA = R ¦ cosA = √R
¦
37.9657350065’’ = √R
· (c=47.3054871141) / cos(A+ ArcTan½)
— Approved:
— There is no significant difference
between any of these in
the PetrieCH6.31 Row32 given
specification,
37.94’’ ± 0.17. The resp.
differences are:
0.0129038928 ¦ B = ArcTan½
0.0185978754 ¦ B = 26° 31’ 23’’
0.0240039644 ¦ B = 26° 29’
0.0257350065 ¦ rJ
All these lie well within the Petrie
given ± 0.17’’.
PHASE2: BpointMAIN ¦
The B-point ¦ PHASE 2 — ORIENTATION ¦
See also from PHASE 1 — The CONSTRUCT FOUNDATION LINE
PHASE 2
first ................. First part: FINDING THE pGpoint
PHASE 2
second ............ Second part:
FINDING THE Petrie Measuring B-point
The B-POINT
Designing the Cheops Pyramid — false
statements are not allowed here ¦ So: If I’m wrong, I have to be cremated. Have
mercy on our souls.
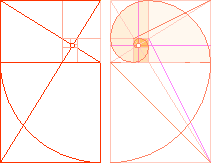
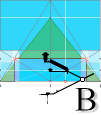
SEE
SHORT INTRODUCTION IN NatCH
PHASE 2
Quantitative
Determination of The Basic Properties
The term CHEOPS
RECTANGLE was adopted by this author after a late
20th century detective search in libraries of the most early known mentioning of
the unique and very geometrical-developing useful connection bd=h². It was
rhetorically used by Galileo Galilei, Apollonios and Pythagoras, further
backwards mentioned as an Egyptian ancient form connected to the Cheops
Pyramid. We respect that tradition here, and adopt the term to it.
Orientation — UpperGS ¦ LowerGS
¦ yATH ¦ yConOFFSET ¦ BUARM ¦ yConBUARM ¦ pGconBuarm
Orientation: Phase2
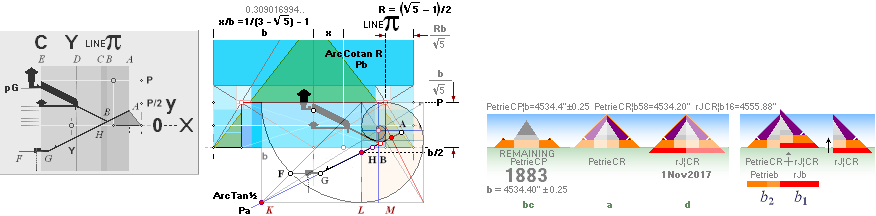
BPOINTmain: Bpoint
GENERAL:
The B-point
connects the rest of the Petrie measured interior Cheops Pyramid design with
the basic Construction Line (The 7 Points). Here we directly find a Petrie (1658.2±0.6) matching/defining correspondence with the
Gallery point (PG) through the two pyramid agents and their combined (related, simple)
quantity results. The illustration below shows the rJCIRCLEcomplex B point
calculated details and the following text explains them, unless already
familiar.
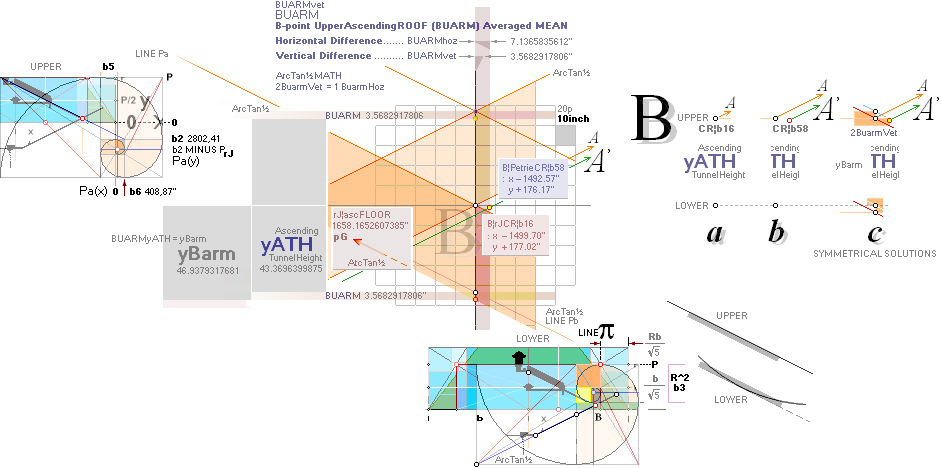
yBarm ¦ yATH ¦ BUARM ¦ PetrieBpoint
DESCRIPTION:
Having
certified the A-point (PHASE1) by the same ENTER entrance on the ArcTan½-line lying and so
genuinely asserting points KLM,
the next
important GS-body paragon xy-position to determine is the B-point:
— The B-point
is the GS-CONSTRUCTIVE
layout’s most crucial intersection point (best to mention in eliminating any
possible misunderstanding): uniting a down and up measuring reference.
— The
B-intersection is ideally Golden Section calculated between the already given
descending passage ArcTan½ and its ascending ArcTan½ spouse, the Petrie named
Ascending Passage upwards in to the Gallery part.
There are
in explicit two differently positioned
GS-candidates showing a visual fit with the ascending passage’s ArcTan½-tunnel:
UPPER:
— One
GS-candidate touches the lower part of the ascending passage, the floor part;
LOWER:
— One
GS-candidate touches the higher part of the ascending passage, the roof part;
— These two are
calculated from the GS-body as follows:
UPPER-GS¦Ascending tunnel roof:
PaLINE →
:
x(Pa) = bR^5 = b6
y(Pa) = b(R
— 1/√5) = b2 — P
:
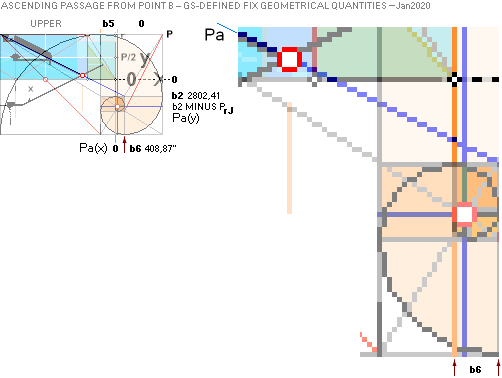
PbLINE →
we borrow these xy from the already given LINExy-values
x(Pb) = Lx —b(R/√5 + R^3) = —(PiLINEx
+ b4)
y(Pb) = Ly b(1/√5 — 1/2) = P — b/2
:
— The LIC line intersecting connection gives the GS
top upper B-point rJCIRCLE¦b16 root ascending tunnel reference xy-values as

Bx —1499.7016293661’’
By 177.0157652488’’
LOWER-GS¦Ascending tunnel floor:
— We only use the xy-position on the GS-body touching
-ArcTan½ ideal geometrically constructive tunnel ascending floor: With this
xy(Pa) point given on the GS-paragon structure, we only have to take its y-axis
intercept (see LIC) and subtract its
value from the already above given xyB-point value (-572.83504943) in order to
receive the offset difference
(The ideal
rJCIRCLE¦CR vertical ascending tunnel height from point B):
— In this
expedition we (try to, with no compromising) use Pa for the upper ascending
negative ArcTan½ and Pb for the lower descending positive ArcTan½ (after
Petrie’s namings).
— For the
trigonometric 0.8 and 0.2 parts, see explanation in b5REF unless already familiar.
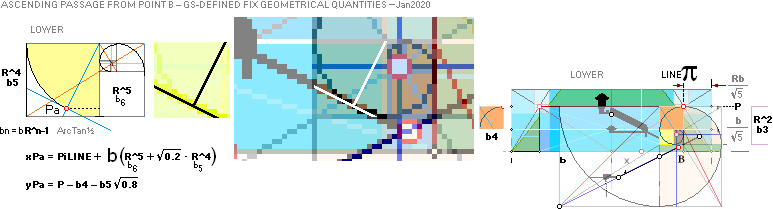
x(Pa) = —b(R/√5 + R^5
+ √0.2 · R^4) = —(PiLINEx + b6 + √0.2 · b5)
y(Pa) = b(1/√5 — R^3
— √0.8 · R^4) = P — b4 — √0.8 · b5
yATH: Ascending
Tunnel Height, ATH
The y-intercept
for this positioned -ArcTan½-line is -616.2046894218’’;
— Taking the
difference gives the rJCR¦b16 vertical construction height

yATH = ROOF¦vert. — FLOOR¦vert. =
43.3696399875’’:
The Construct LayoutAscendingTunnelHEIGHT from point B —
AscTunHEIGHT,
here denoted
yATH:
yATH = 43.37’’ — rJCR¦b16-determined
= 43.3696399875’’
We mark this
value as The Basic Nominal Constructive value for the ascending tunnel height.

BUT:
We would be, really,
The F-Word up if this would be the final GS-constructively suggested result.
— What’s the
hang?
— We need an
additional BUARM — for securing
the Gallery Top Slope PG-point.
— A B-point Upper
Ascending ROOF (BUARM) Averaged MEAN.
We study that.
First: Adding the yConOFFSET — for
pending comparing purposes
The yConOFFSET is a fix property that can (possibly) be
used in our further testing quantities. We study how.
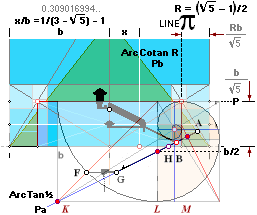
we already have
the rJCR¦b16 xyG-coordinates:
— Taking the
corresponding PetrieCR¦b58 coordinates establishes the actual construction plan
— here to be investigated in deep. Selecting a ”1” in the calculus card we
receive the comparing corresponding PetrieCR¦b58 values as follows:
yConOFFSET:
See details in ConAG
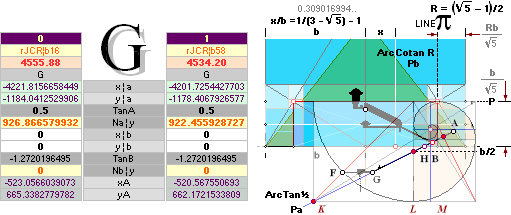
These two are
connected by a fix, solid exact internal xy-horizontal-vertical differing
separating offset value. Their y-intercepting non alterable constructive
difference is
G(rJCR¦b16)Ny — G(PetrieCR¦b58)Ny =
![]()
yConOFFSET =
4.4106512044’’
BUARM: With a
PetrieCR¦b58 4534.20’’ ideal Cheops Rectangle corresponding ascending quantity
design layout, we have the B-point references for the upper ROOF part from the
only two available construction coordinators rJCR¦b16 and PetrieCR¦b58 as
BUARM: BUARM ILLUSTRATED in BPOINTmain
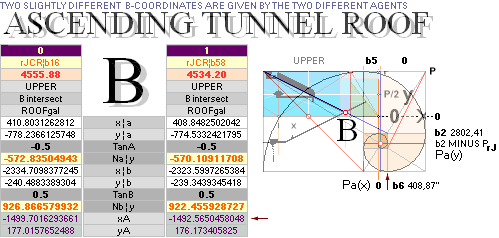
TWO SLIGHTLY DIFFERENT B-COORDINATES ARE GIVEN BY THE TWO DIFFERENT
AGENTS
(|x1| — |x2|) =
7.14’’ → ![]() ;
;
[xATH(rJCR¦b16) — xATH(PetrieCR¦b58)]/2 = (1499.70 — 1492.57)/2 = 3.57’’,
meaning:
— On the
ArcTan½ right angle triangle: (x1 — x2) ½ = (y1 — y2):
— 3.57’’
is an exact (2 decimal rounded) geometrical BUARM,
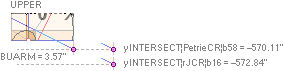
B-point UpperAscendingROOF (BUARM) Averaged
MEAN Vertical Difference between the
two pyramid construction agencies rJCR¦b16 and the ideal Cheops
Rectangle PetrieCR¦b58:
»best provision».
BUARM = 3.57’’ = 3.5682917806’’
Options — see The AG-Condition:
— In general (result from the AG-condition): ONLY the
rJCR¦b16 pyramid agency will have priority on a fixed geometrical parallel
relationship with the ideal PetrieCR¦b58 spouse. Meaning:
— The ideal
PetrieCR¦b58 agent CAN make ”averaging means” together with the main
rJCR-agent.
Meaning:
— EXTENDING OUR
simple and direct POSSIBILITIES
(for us to find, and the constructors to form) in finding true (and exact)
quantitative matches with the real physical PetrieCP Cheops Pyramid measurements from 1883.
yConBUARM: yCon ¦ BUARM ¦ tyATH ¦ aVA ¦ Con ¦
yBarm ¦
yBarmILLUSTRATED
The GS-body then SUGGESTS that the
B-point with agent PetrieCR works like this:
— AS the agent
PetrieCR has no other possible parallel relationship with agent rJCR than in
the G.point determination, see conAG, we use agent
PetrieCR to give us an ADDITIONAL AVERAGED MEAN from
• (y1 — y2)/(x1 — x2) = ½ for the
PetrieCR¦b58 ROOF -ArcTan½-line, so that
• (y1 — y2) = (x1 — x2) ½;
— (x1 — x2) = 2
BUARM =
= 7.14’’
= ![]() ;
;
Given an
x-value on a right angled ArcTan½-triangle, the y-value appears as a simple
x/2:
• [(x1 — x2)/2=3.57’’
= BUARM
+ (yConOFFSET=4.41)] / 2 = averaged VERTICAL ADDITION mean value:
aVA = 3.99’’;
The
GS-SUGGESTED Pyramid nominal CONSTRUCTION (Con) VALUE,
yATH-value (43.37’’), will then have
a longer
(OPTIONAL) version added with aVA as a total (t)
tyATHyConAssociate =
43.37 + 3.99 = 47.36’’ = yATH + aVA.
Total vertical
(y) distance RoofFloor Ascending TunnelHeight:
tyATHyConAssociate
....... = 47.36’’.
— In figures,
this VERTICAL value is nearly the same as (HowPetrieReck) the PetrieCH6.31 measured/calculated PARALLEL descending
entrance value (e=) 47,36’’:
— This tyATH
result 47.36 value has no further meaning or use here, as we know of.
With only the
addition of BUARM — we leave yConOFFSET and
aVA — we have
tyATHyBUARMAssociate ... = 46.94’’ = 43.37 + 3.57 = yATH + BUARM = yBarm:
Which we name
yBarm = 46.94’’ = yATH + BUARM = 46.9379317681’’;
yBARMillustration: BUARM ¦ yPonB — Addition to SIO and yConB — ¦ yBlow ¦
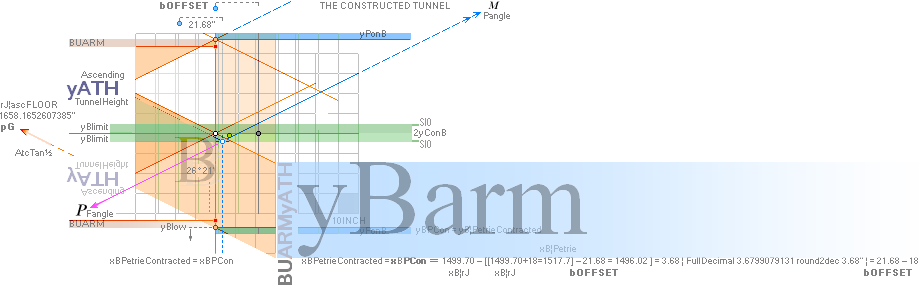
THE CONTRACTED CONSTRUCT view.
SEE also part ILLUSTRATION
IN TheConstruct and partly in GalCalcOW1. Here with
some additional details (yBlimit ¦ yConBoffset ¦ yConB) for the
proceeding:
As we know: the yConOFFSET quantity no longer
has any specific role to play from
here apart from its fixed ConAG property as a
pyramid agency.
+ 43.37 ......... = yATH
+ 4.11 ........... = yBlimit = yConB + yConBoffset = yConHBALimit
= yConB + SIO
+ 3.57 ........... = BUARM
+ 1.84 ........... = [ bOFFSET — 18 ] / 2 = yBPcon — trivial Result from
bOFFSET contraction
———————
= 52.89 = cSIDE
/ √1.25
= 47.31
— The
difference in leaving yConOFFSET and aVA is 0.42’’
— The yB associated
yBarm y-ccordinate then becomes
(yB=177.02) —
(yBarm=46.94) = 130.08’’ = yBLow;
yBLow = 130.08’’ = yB — (yATH + BUARM =
BUARMyATH = yBarm)
With these parametric
contributors we can make a full test on the Gallery sloping floor top, the
vertical midpoint of the Pyramid, for comparison with the Petrie measured
values:
pG(Con) and
pG(BUARM): yATH ¦ BUARM ¦ yConBUARM ¦ yConOFFSET ¦ yPG ¦ yPGcalc
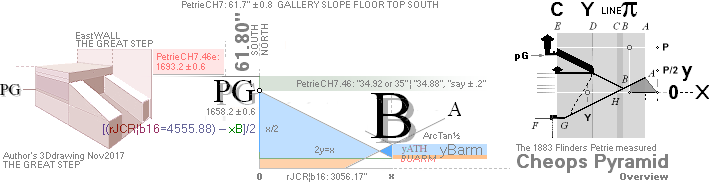
PetrieCH7.46 Col1 Row18 gives only an indirect
pG-point value:
He refers the top step surface by [PetrieRow42]
1693.2’’ ± 0.6 with a
below step face socle height value as ”34.9 or 35”, or [PetrieRow34]
34.88 ”above actual floor end” depending on detailed more or less
injured location. Summing these figures, and caring on Petries tolerance
specification makes an allowed Petrie1658
—35+1693.2=1658.2 with the
vertically Petrie mentioned 1693.2 adopted tolerance: ± 0.60.
— Using only the BUARM
y-offset 3.57’’ + yATH(43.37) = 46.94’’ = yBarm we have [ArcTan½
triangle x/2=y]
y(PG) = 1658.17’’ — only 0.03’’ from
Petrie’s nominal:
yPG¦rJCRb16 =
[(rJCR¦b16=4555.88) — 1499.7¦xB]/2
+ 177.02¦yB — 46.94¦yBarm
= 1658.17¦1658.1652607385
— Both end values
lie well within Petrie’s given tolerance ±0.6. See also The TRANSPOSITION EQUIVALENT.
In
expliocit: Petrie’s socle height (35’’) is rJCIRCLE identified with an
ideal single value
50R + yBlimit = 35.0129561608’’ = 30.9016994375 +
4.1112567233. And so Petrie’s level 1693.2 is rJCIRCLE identified as
yPG + 50R
+ yBlimit =
1693.1782168993’’ rounded 1693.20’’. Same identity.
— Approved.
yPG rJ-calculated
from B point: ![]() [(rJCR¦b16=4555.88) — xB]/2 + yB — yBarm = 1658.1652607385 → 1658.17’’
→ 1658.2’’: ArcTan½-math: Petrie 1658.2 Quote:
[(rJCR¦b16=4555.88) — xB]/2 + yB — yBarm = 1658.1652607385 → 1658.17’’
→ 1658.2’’: ArcTan½-math: Petrie 1658.2 Quote:
1658.20 ± 0.6.
The rJCIRCLE complex calculated yPG
level value
1658.17’’ = yPG = 1658.1652607385’’
→ 1658.20’’.
ArcTan½-math: .............. (b1 + b1xB)/2 + b1yB — [yBarm = yATH + (BUARM=GSintersectionDiff)] = 1658.1652607385’’ ....... rJCR¦b16 = b1
APART FROM
OTHER POSSIBLE CANDIDATES this result is — as known here — the closest we can get
to the Petrie corresponding nominal yPG = 1658.2’: Difference 0.03’’ — in
allowed ± 0.6’’. A direct hit.
There was also another (near close,
approved) match along with the above two — see FIRST.
PHASE 1 — THE CONSTRUCTION LINE ¦ PHASE 2 — THE B POINT —— Phase2.1 — FINDING THE pGpoint ¦ Phase 2.2 — FINDING THE Petrie
Measuring B-point
ConMes: CONSTRUCT
AND MEASUREm overview
The Construct and The Measure
THE
CONSTRUCT AND THE MEASURE — just a short overview
How
The 7 Points Determined
Construction B-point appears
— Construct and
Measure have different preferences: The Construct is impossible to deduce from
the Measured building quantities the underlying rJCIRCLE complex is understood:
the construct plan.
See also further below in Explaining
the Construct.
TheConstruct@B — BASIC: THE yCON OFFSET VALUE BETWEEN THE TWO PYRAMID
AGENTS IS PRESERVED.
yConOffset DETAILS IN ConAG.
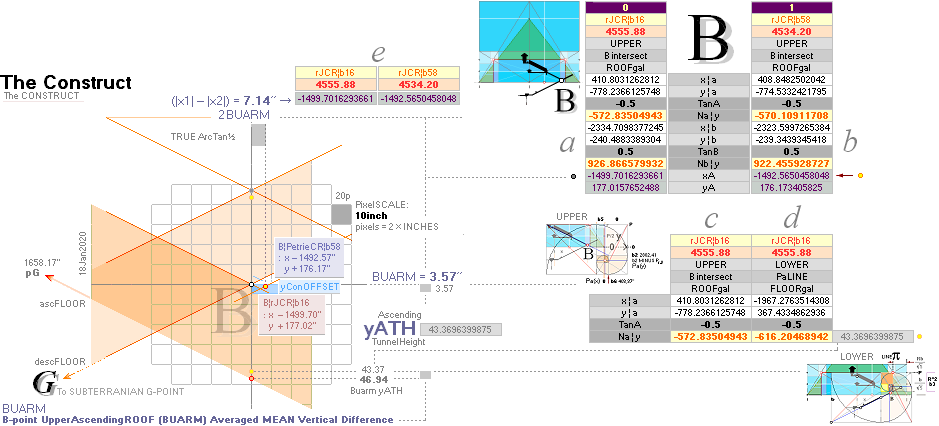
————————————————
ab-values from GS-paragon UpperGSroof on comparing
rJCR¦b16 and PetrieCR¦b58. cd-values
from UpperGSroof AND LowerGSfloor. e-values from the ab-set.
See in explicit
The pG-value calculation
via B,
The TRANSPOSITION B.PG.
TheMeasuredConstruct@B
— Petrie point B:
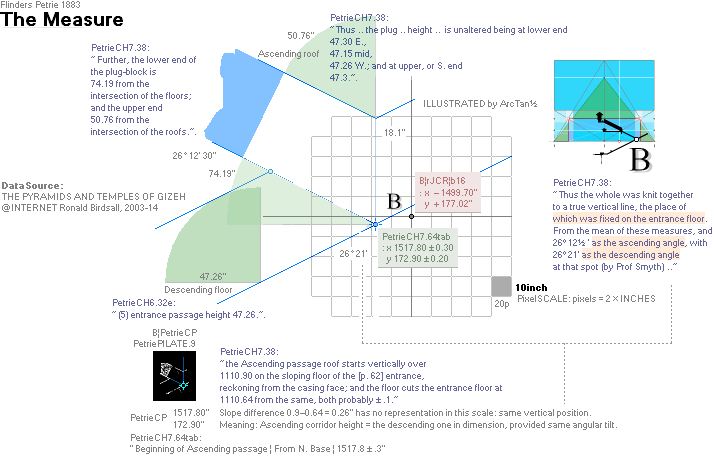
See further below in Explaining the Construct and ThePush.
— The numbers 50.76 and 74.19 is
mentioned (quote continues PetrieCH7.38):
” Further, the lower end of the
plug-block is
74.19 from the intersection of the
floors; and the upper end
50.76 from the intersection of the
roofs. Having thus fixed the beginning of the Ascending passage, by the point
where its floor produced onwards intersects the floor of the entrance passage,
we can proceed up the Ascending passage from this as a starting point.”.
NOTES ON PETRIE’s VALUES IN tunnel
POINT B — missing data?
— No. But a clarification in needed
here.
PetrieCH7.38:
”.. with
26° 21' as the descending angle at
that spot (by Prof Smyth),
the Ascending passage roof starts
vertically over
1110.90 on the sloping floor of the
[p. 62] entrance,
reckoning from the casing face; and the floor cuts the entrance floor at
1110.64 from the same, both probably
± .1.”. No clue.
” The junction of the passages was
not projected over the broken part uncertainly, as had been done before; but a plumb-line was hung from the W. side of the
Ascending passage roof, in front of the plug-blocks; and measures
vertical, perpendicular, and sloping, were taken to the plugs, the fragments of
the ascending, and the top and bottom of the
entrance passage. Thus the whole was knit together to a true vertical line, the place of which was fixed on the entrance floor. From the mean
of these measures, and
26° 12½ ' as the ascending angle,
with
26° 21' as the descending angle at
that spot (by Prof Smyth), the Ascending passage roof starts vertically over
1110.90 on the sloping floor of the
[p. 62] entrance, reckoning from the casing face; and the floor cuts the
entrance floor at
1110.64 from the same, both probably ± .1.”. No clue.
In dissecting Petrie’s statements in
parts an answer shows up in full:
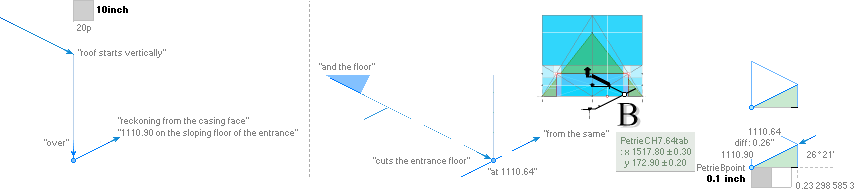
The
illustration clarifies the aim:
— There is a
small difference (not visible in the 10 inch scale) between
the roof
(AscendingDescending) intersecting point
vertically
aligned with the Petrie xyB-point from PetrieCH7.64tab
xB¦1517.80±0.30
yB¦172.90±0.20
and the floor
intersecting point (AscendingDescending):
— The latter is
pushed 0.26’’ up-ways north the entrance.
HOWEVER:
PetrieCH7.64tab gives for the xB-coordinate the measuring tolerance
± 0.30, which
obviously overrides the
0.26’’ floor up
north intersecting deviation (horizontal 0.23’’ through the angle 26° 21’).
— So: From our
Cheops Rectangle investigation viewpoint, the Petrie noted UpNorth 0.23’’
horizontal difference will have no effect on this expedition — unless other
arguments will show up.
Petrie F° Angle:
— The actual physical [mean averaged] floor angle between subterranean [P] and
Petrie’s B-point where descending meets ascending — compiled 27Feb2020
THE
ACTUAL PHYSICAL descending FLOOR ANGLE(s)
The FANGLE
ArcTan(yG — nVALUE + yB — yBlimit)/(xG
+ 10R — xB — 18) = 26.5479489261° = 26° 32’ 52.61 61 34’’
THE
COMPOSITE ANGULAR COMPLEX — The yPonB secret
AS IT
HAS SHOWN:
How
the descending tunnel HAD to be constructed physically in order for the Petrie
working group to get a spot on (TCA, see full Petrie Quote) The Central Aspect: the 19th floor and its
decisive projective connection to the descending passage — exactly by a TCA
principle as described by Petrie.
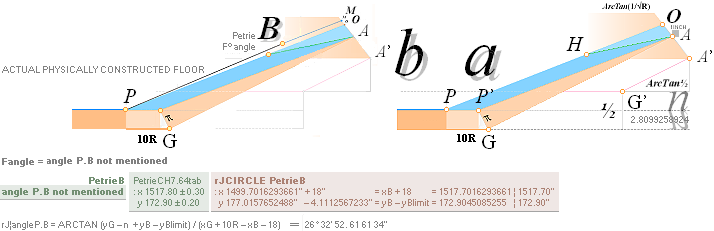
a: The
Construct’s Plan: If this would be the final cut, the actual Petrie measured
values would be catastrophic.
— Why
is that?
b: Spotting the
Casing Rim (O) from the tunnel (P or H) would clearly miss the point if the
tunnel floor would finalize on the line PO of the a-construct planning
level: Petrie’s Cogitated Principle (See full Petrie Quote) with the 19th floor level;
— Its
block course masonry thickness — at the level of the entrance — features a
trigonometric/optical PROJECTION (The TCA principle):
THE CENTRAL ASPECT:
The Whole Inner Design Pyramid Plan
Cheops Pyramid — SEE THIS CENTRAL PROJECTING PRINCIPLE
MORE IN DETAIL FROM PETRIE’S DESCRIPTION IN PetrieTCA.
A UNION
APPEARS between descending passage and actual course.
In other words:
— Some additional floor height (Fangle) of the a-construct
planning level is needed to GUIDE a measuring optical instrument AT
the actual Petrie measured/observed Casing Spot:
— The
yPonB quantity:
THE yPonB quantity secures a safe optical lower
limit visual sight line window through the descending passage through which
safely spotting the decisive Petrie PC point on the Pyramid casing rim. See
full details from ENTER.
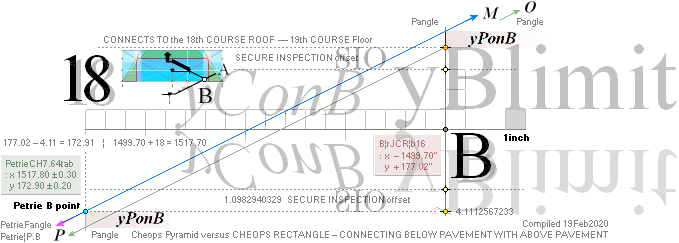
So?
—
What MATHEMATICALLY SHINY INSTANCE COULD PROVIDE such an ”additional floor
height” above the actual construction plan for the Cheops Pyramid building?
BY EXACT MATHEMATICAL GEOMETRICAL DEFINED
QUANTITIES:
— The
rJCIRCLE definition of the Petrie measuring B-point (The
Petrie B point):
PROOF:
—
Using intersection mathematics — same as optical sight line intersections — on
the acquired different angles (Fangle, Pangle and Hangle) from the given defined Petrie measured values with
Petrie’s given tolerances, defines a narrow Pyramid casing visual optical
window between the MO points as compiled below.
SEE ALSO THE nVALUE FROM ENTER: yA + nVALUE = 19th FLOOR vertical
level: 668.1482038706’’. PetrieCH7.35: ”668.2 ± 0.1”.
OVER AND OVER AGAIN, WE FIND THAT THE rJCIRCLE calculated quantities DO — well —
define Petrie’s measured values as taken within the Petrie specified
tolerances. See also IntroEX.
The
Petrie spotted point pA — Petrie’s instrumentally claimed Pyramid
original casing point on the 19th course floor level — has the Cheops Rectangle
Pyramid Ideal Casing point O as an absolute lower visual sight line along the
actually constructed descending floor, as the rJCIRCLE construct plan is
explained through this result.
— The
upper limiting sight line from Petrie B to the casing rim surface guarantees a
narrow optical spotting window framing the decisive point pA. The metric
casing difference between the lower
floor spotting limit and the actual pA point extension is no more than
0.23’’ (roughly and ideally slightly less than [0.25’’]/√1.25=0.2236’’) —
provided an ideal flat B.M even precision tunnel floor with no deviations.
So:
— The
whole angular and coordinate/measuring point descending passage complex can
(now, finally) be viewed in the following more precise detail:
STRONGLY EXAGGERATED
ANGLES FOR CLARIFYING THE EXPLAINING CONSTRUCT PICTURE: General tunnel angles
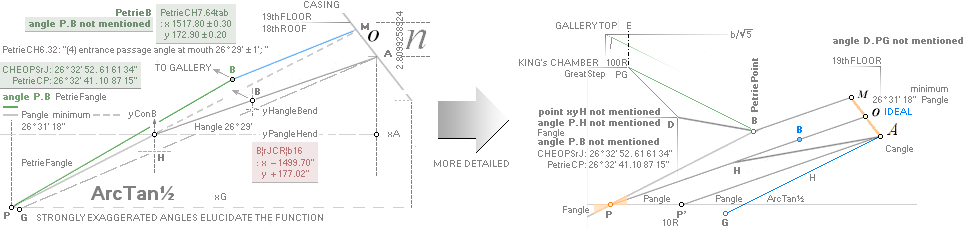
SUMMING:
— All
construction planning in detail. High Tech Math.
— But
what if the old modern academic Egyptians who are said by these more modern
inventors to have built the devise were psychic: they knew all these features
directly from Within?
—
Happy them. We are outclassed. Shredded. I am so sorry for having taking up your
precious time.
Aftermath — at
first, during some time ..
IN Attempting
to compose an overall describing picture of the Petrie given angles and
measured points of the descending tunnel between casing (A) and tunnel end (P),
nothing made sense.
So it was until a specific Petrie F°angle
(Fangle) was identified between the Petrie measured points: the subterranean
(P) and, nearest mentioned above the pavement, point B:
— Petrie
neither mentions any measured connection (from the subterranean site) to the
in-between lying H-point — the point where the descending tunnel meets the
pyramid’s baseline.
Petrie’s
FloorAngle P.B — Fangle, the actual physical floor, as here understood — is
never [directly] mentioned in any angular value in Petrie’s Chapter 7 descriptions.
— Reckoning the
Petrie xy coordinate values between
4228;1181 and
1517.8;172.9
gives Fangle =
26° 32’ 41’’
— slightly
different from the general Petrie 4140 inches long descending passage stated
thoroughly averaged mean
”26° 31’ 23’’ ±
5’’ ?”.
ExCon: TheConstruct
EXPLAINING
THE CONSTRUCT IN QUANTITATIVE DETAIL
The Construct — in detail
With given P angle (»Pangle») and H angle
(»Hangle») the floor
offset construction points can be calculated — exactly.
Pangle and Hangle define
THE DESCENDING PASSAGE FLOOR
CONSTRUCT LAYOUT ANGLES:
— See how The Petrie Point explains why a
descending FLOOR BREAK (@H) must exist
to connect the Construct Plan to the
entrance point (A), thereby granting the main construction line to be buried
inside the building, never exposed in the actual visual edifice construct.
The descending and breaking floor
construction trimming reference values will then appear directly as follows:
yConB: ExCON
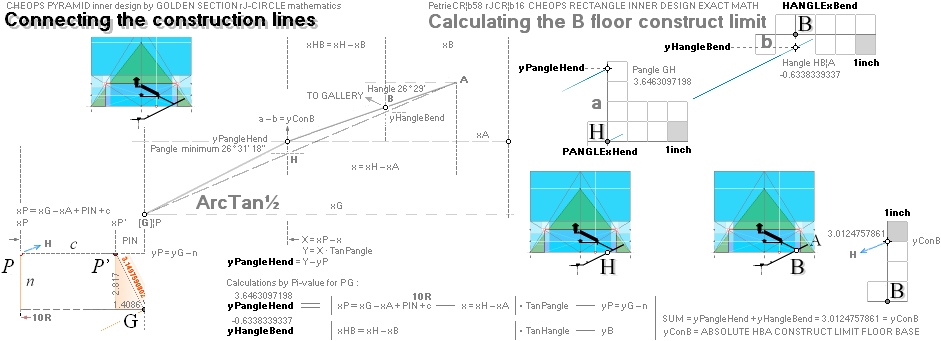
yPangleHend — yHangleBend.
THE DESCENDING FLOOR SLOPE will be
constructively determined from the Petrie P point (P) through the P angle (lowest Petrie
26° 31’ 18’’).
Through the floor breach @H, the
floor directs to the entrance point A though the slightly smaller H angle (Petrie 26°
29’ ± 1’).
Summing the continuity of this
floor-construct gives a reference point yConB @B valued
yConB =
yPangle@H-end + yHangle@B-end =
3.0124757861’’ = yConB
above the nominal rJCR¦b16
calculated yB-value yB = 177.0157652488’’.
— We will see how this point CAN
rJCR¦b16-DETERMINE the actual Petrie B- measuring point which connects the
Petrie measuring descending and ascending passages.
rJCR¦b16-DETERMINATION
THE
ACTUAL PETRIE B- MEASURING POINT
rJCR¦b16-DETERMINATION of the actual
Petrie B- measuring point
is realized as follows — it all
connects to the Petrie 19th stone masonry course, 18th course roof value
(Petrie 668.2’’ ± 0.1):
yConBoffset:
n — D = 1.10’’ ¦ FOR PREFIXxSIN, SEE TRIGREF unless already
familiar ¦ Finding
d ¦ THE D-FORM IS THE SAME AS THE ONE USED IN ADD1.84 ¦ yConB
yConBOFFSET = SIO = 1.0982940329’’:
EXPLANATION — the yConB-offset
finishes the entrance passage construction math:
— The Petrie stated descending slope
angle P-point related ”26° 31’ 23’’ ± 5’’ ?” travels by distance d (Finding d: 2.13236805’’,
see table Result
Basics), ending on the ideal Cheops Rectangle Golden Section
Casing Pyramid near point A;
COMPLEMENTARY EXPLAINING
CONNECTIONS: yBlimit = yConB + SIO
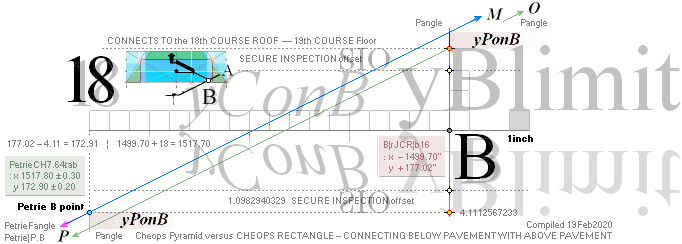
The Petrie F°Angle — Line
SubterraneanPetrieP.PetrieB as known: never described by Petrie himself in
terms of a specific angular value — is described in a separate section. See Fangle. This illustrations clarifies how
the constants yBlimit = yConB + SIO appear from the yConB angular connections between details
below and above [H] the pyramid baseline reference [Petrie’s
pavement], here at point region B.
— yPonB is apparently a constructive BONUS.
SecureInspectionOffset,
SIO: D18 ¦ yConBoffset
— As the bottom passage G-region n-value (hypo side in the ArcTan½ triangle) through the
adopted pi-value in calculating the P-angle is
π/(1.25)^½ = 2.8099258924’’,
also equal to
the Petrie’s measured 19th course floor value 668.2’’ ± 0.1 by
(yA¦rJCR¦b16 =
665.34’’) + [π/(1.25)^½ = 2.81’’] = 668.15’’ ............... Well APPROVED,
»we» CAN use this additional
»fillOut» d→A projected difference
n — (D=1.7116318595 — on Casing point A) =
1.0982940329’’ =
yConBoffset = SIO = n —
»D18»
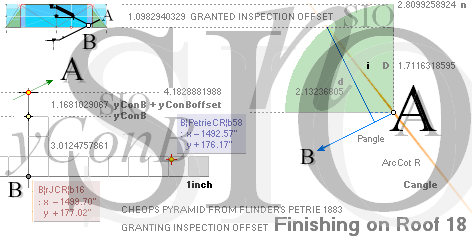
SIO = 1.0982940329’’ ................................ yConBoffset = SECURE INSPECTION OFFSET, SIO
as an »inspection guard» or
A GRANTED INSPECTION OFFSET — A
»The» decisive Petrie observing LEAD:
— See detailed in Proving the 19th ¦ yBarmILLUSTRATION ¦ TP1DET .
yBarm ILLUSTRATION ¦ TP1Det ¦ Course
thickness D — Proving the 19th
— See also The Petrie Quote in How Petrie Reckoned the Entrance Geometry, the central
”The crucial
test then is, supposing the passage prolonged outwards till it intersects this
course, how will its end, and the face of the casing, stand to the casing stones
at the foot of the Pyramid?”
— from the 19th course floor height
(668.2’’ ± 0.1), Everything in the inner design of the pyramid, all the
measures, depends on the onset of that measure.
yBlimit SIO
— Adding the SIO=yConBoffset value to the
yConB-point gives a final
4.1112567233’’ = yConB + yConBoffset =
yConHBALimit = yConB + SIO = yBlimit
yBlimit = 4.1112567233’’ = yConB + SIO
............ SECURE CONSTRUCT ENTRANCE PASSAGE
FLOOR LIMIT @B, yBlimit
on top of the yB = 177.0157652488’’
value.

So (again):
— What is the meaning of this
yConHBALimit = yConB + yConBoffset?
— Obviously the simple Petrie
introducing Main Measure:
The (Constructors) meaning is obviously to arrive at a measuring ENTER SPOT of the 19th course floor value
— AT some Petrie staircase masonry remaining sloping angle:
— The PetrieCh7.35: 51° 53’’
28.60’’: the Petrie Cheops Pyramid remaining staircase masonry sloping angle at
the northern entrance site as seen/measured with respect to the whole tunnel.
— The yConB part 3.01’’ from
the H-floor breach @B, plus the additional remaining SIO 1.10’’ yConBoffset, FILLS UP
up the remaining space to the 19th course floor — on the Petrie (idea of the
original) Casing, as he mentions it (”.. and
the face of the casing ..”, see the entire Quote).
RelatedPetrieSPOT:
yBlimit
In Short:
— (Vertical) OFFSETS (by given angles) above the construction
plan must be given in order to secure a safe (and precise) measuring spot on
the Pyramid casing as seen from the tunnel: the projective connection between
descending passage and the 19th course floor and its masonry height (37.94’’) at the level
of the entrance.
See in detail from Proving the 19th ¦ Enter ¦ Fangle ¦ PetrieCH6.31 whole Quote .
Or as Petrie states the general
status of (some parts of) the edifice himself
(Quote from another
web site):
”.. it is to be compared to the
finest opticians' work on the scale of acres.”.
The Petrie
B-point. Phase 2.2: — PetrieBpoint: RELATED PETRIE SPOT
The final Test: The Petrie B-point
PHASE
II.2: FINDING THE Petrie Measuring B-point — no dramatic issue
See also PHASE II.1: The B-point FIRST PART

In PetrieCH7.39¦64tab
Petrie gives the xy(B) values
xB 1517.8 ±
.3
yB 172.9 ±
.2 ............................ website source corrected from
table error. Petrie gives correct value in CH7.39
We [PHASE 1—Table Results] calculate the corresponding rJCR¦b16 agent values from the previous results and
arrive at
xB: 1499.70 + 18 ...................... = 1517.70 ............... approved ¦ Petrie: 1517.8 ± 0.3
1499.7016293661 + 18
................. = 1517.7016293661
yB 177.02 — 4.11 ...................... = 172.91 ................. approved ¦ Petrie: 172.9 ± 0.2
177.0157652488 — 4.1112567233 ... =
172.9045085255
— We get smaller deviations
depending on reckoning with or without decimal cuts.
These values are obvious DEFINITIONS
of the Petrie measured values — or CAN be understood as such.
— We can most freely use any of
them, Petrie measures or those via the rJCIRCLE complex.
— They give the same result anyway —
within the Petrie given measuring tolerances.
The previously given two SIO and yBlimit 19th course floor coupling descending
floor quantities lead to a rJCR¦b16 definition of
THE PETRIE ESTABLISHED CORRESPONDING
MEASURING B- point:
The decisive B-point is the place
from where Petrie unites the descending tunnel with the ascending one, leading
further south up to the named Grand Gallery and the two chambers.
— As the Petrie measures in this
expedition by all means are LEADS and HINTS to a SIMPLE construction plan, if
at all, the remaining is/becomes more or less ”a walk in the park” — provided
familiar with TNED. See 18 in explicit
unless already familiar.
Petrie B
point: See also COMPLEMENTARY in yConCompl.
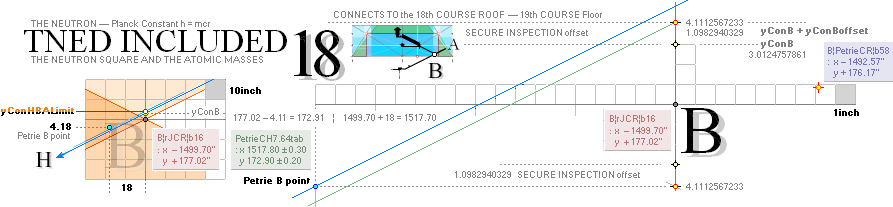
This FIT suggests that the constructors
of the Cheops Pyramid had TOOLS with some extraordinary today obviously unknown
capacity in executing extremely high precision constructs from prepared huge
pieces of (cut) rock.
— Practically »no tolerance at all».
The building has been standing there a long time along with earth quakes,
obviously taking not too much hurt in suggesting silly tips, leads and hints of
how it came about.
Approved:
— The Petrie decisive measuring B
point is rJCR¦b16 defined.
— What is so special about ”the number
18”? FullAnswer.
SEE
THE NOW (Jan2020) AVAILABLE ENGLISH VERSION OF A GENERAL OVERVIEW OF THE
CONTENT IN UNIVERSE HISTORY here in NatCH.
—
It’s all about mathematical physics in electricity, magnetism, induction and
gravitation: nuclear physics at the level of absolute highest possible
precision. We deal with all the fundamental most important parts with examples,
quotes, comparisons, references and critical evaluations and aspects where
possible: Faulty statements are NOT allowed here. The overall mission is:
EXPLANATION. Zero speculations. We expose all the thorough DEDUCED connections,
and explain how they are derived and how they connect to the absolute basic
physics and mathematics — or not at all. The reader is the judge. Always
has been.
We continue.
TheSeal: ThePush 1 ¦ ThePush 2
The Petrie Ascending Angles
HOW THE CONSTRUCT BECOMES »SEALED»
A
sealing property appears directly through THE
TWO PYRAMID AGENTS
THE rJCR¦b16 base offset 21.68’’ PUSH:
Having now determined all the basic
inner design quantitative Petrie value corresponding measuring points
entrance passage tunnel G H B A
coordinate points with
Pangle and Hangle, all the constructive layout
properties connected to the ENTER entrance
(nothing here mentioned on the two chambers except in R-multiples),
»it’s time to SEAL the package»:
— This author TAKES »the
constructor’s role» to explain the details WHEREAS these already are obvious
(or, if faulty, this author has some serious issues):
— With
the established GS-body pyramid agents
rJCR¦b16 and
PetrieCR¦b58 and the quantities we have derived and deduced from them and their
actual mutual xy pyramid offset values
![]()
The offset values vertical-h horizontal-b between
the two pyramid agents PetrieCR¦b58 and rJCR¦b16
we (find — can relate — a
corresponding geometrical, not actual physical) PUSH
the PetrieCR and its corresponding PetrieCP into
the rJC¦b16 agents Acquired values.
Meaning as obvious:
impossible to deduce except through
a corresponding TNED
rJCIRCLE knowledge
— No PhD whatsoever or any body else
in this or any other Universe will have a slightest smallest tiniest itty,
bitty, tiny chance of DEDUCING the Edifice from a Golden Section Paragon geometrical
Mathematica structure UNLESS acquainted with (a corresponding) TNED: THE DEDUCTION OF THE ATOMIC
NUCLEUS → The rJCIRCLE: max neutron
density.
— And what, exactly, would be the
point in that?
Very Educated Population these days, big wall TV and the kind .. dying
trees ..
School Student’s favorite subject:
mathematics. MustBuyBook. Joy everywhere.
— Maybe we will
find a brilliant answer in Natural
Tenderness.
Returning to the building: The Device.
— IT has (now, as explained) become
SEALED — granted protection from inspection, unless so understood — until TIME
would come with a revelation: someone willing and motivated enough to dig for
better answers than those coming from modern quarters.
Feel free to argue — knowledge to all for free.
ThePush1: PetrieBpoint ¦ TeSeal ¦ xBPetrieContracted — See lead illustration in BPOINTmain
PART
I OF THE SEALING PUSH
THE VERTICAL HEIGHT of the ENTRANCE
PASSAGE
THE
ACTUAL Pyramid CONSTRUCTED Petrie measured QUANTITY
The
two pyramid
agents b1 and b2
— b1
as the rJCIRCLE Cheops Rectangle (CR) agent rJCR¦b16 and
— b2
as the actual Cheops Pyramid Cheops Rectangle agent PetrieCR¦b58
compose
a delicate quantitative geometrical bOFFSET=21.67’’ horizontal PUSH.
— The
PUSH is centered in the junction between the descending and the ascending
passages in point B.
— The
two pyramid agents horizontal push into each others quantities exposes a SET of
perfectly defined CONSTANTS leading to a definition of the Petrie measured —
and discovered — pyramid casing principle (Petrie19thProof): The Pyramid Casing Connection to the descending
passage from the casing entering point.
— See
also from ENTER.
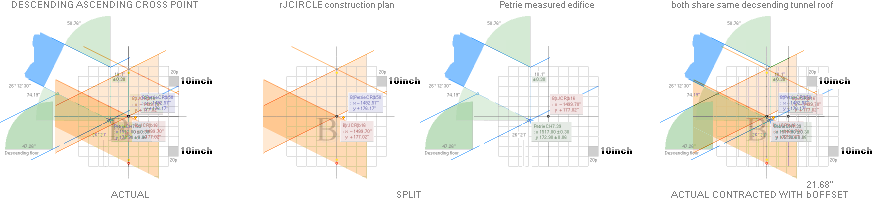
Contracted by the two pyramid agents
mutual half pyramid base quantity, the two sets ideally share one and the same
descending roof. Useful Quantities are generated from that position.
THE
ACTUAL HORIZONTAL OFFSET CONTRACTION between the two agents is illustrated as
above, with a more detailed description below.
— We
(now, finally) DIRECTLY understand why and how it is IMPOSSIBLE to deduce or
even ”find” any PLAN for the building — UNLESS the two agents are discovered:
—
Their ROLE, function and precise quantities.
These showed up through the simple rJCIRCLE
complex introducing test (Nov2017)
which soon unveiled the whole secret. And it has, since by further deduction,
contributed to a profoundly clarifying picture of the whole edificial plan.
—
Flinders Petrie and his 1883 measuring working group is responsible for this
discovery. No doubt. See further TCA.
In projecting the two pyramid
agencies IN THE B-POINT REGION
on the
rJCR¦b16 b-value .............. 4555.88’’ offset in-push 21.68’’ relative the
PetrieCR¦b58 b-value ...... 4534.20,
including the Petrie given measures
in the same B-region
+ 43.37 ......... = yATH
+ 4.11 ........... = yBlimit = yConB + yConBoffset = yConHBALimit
= yConB + SIO
+ 3.57 ........... = BUARM
+ 1.84 ........... = [ bOFFSET — 18 ] / 2 = xB¦Petrie — xB — bOFFSET —
18
———————
= 52.89
/√1.25
= 47.31
bOFFSET — 18 =
[xB¦rJ=1499.7016293661] — [xBPetrie¦rJ = xB¦rJ+18=1517.7] — bOFS] = bOFS — 18 =
xBPetrieContracted.
it seems directly obvious (in this
illustrative 10 inch scale) that they
the PetrieCP values and
the JCR¦b16 values
share one and the same tunnel roof
of The Descending Passage. Exactly.
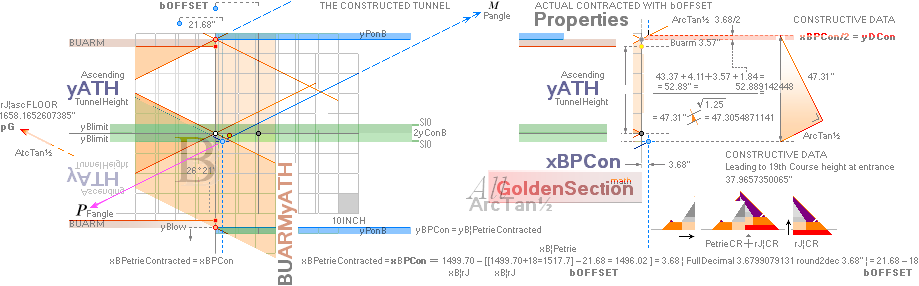
We — obviously — need to relate
these details thoroughly unless we prefer to idealize — invite — some less
shiny suggestions from Trouble Understanding Concept Enterprises: it IS old.
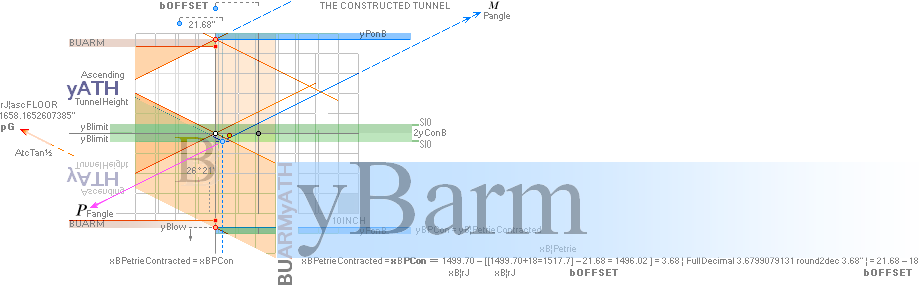
These two figures above and below
show complementary different denotations used in this deducing part and its
development (ATH: Ascending Tunnel Height; BUARM: B-point UpperAscendingROOF
Averaged MEAN).
Especially in concern of the precise
quantities, the illustration (TransPond) below explains — proves/exposes —
some of the profound ideation behind the construct: how constants in the lower
(B point) part are reused in defining constructing properties belonging to the
upper (Gallery) part.
— R = (5^½ —
1)/2 = 0.618033988.., here The Golden Section Relational Constant. See also The ArcTan½: everything in the Golden Section Cheops Rectangle (Cheops Pyramid)
construct plan connects to its simple right angle triangle.
The figures below show the separate
PLAN from the rJCIRCLE
complex, left, and part of the actual physical Cheops Pyramid
CONSTRUCT from Petrie’s values, right.
The PUSH-contracted parts: PLAN
and Construct
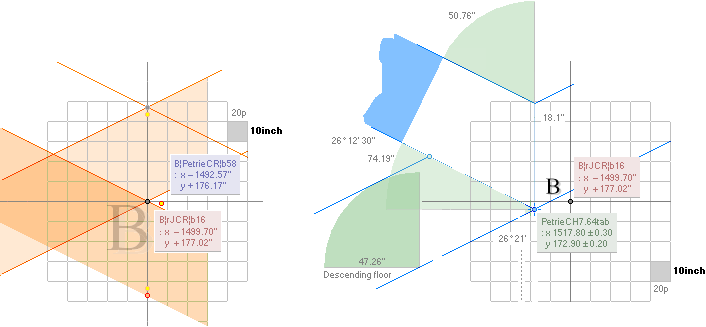
The two above parts are shown
complementary more in detail as actually horizontally contracted by the pyramid
½ side pyramid
agents offset 21.68’’. That contract gives a resulting set of
profoundly vertical exact constants leading to the definition of the 19th
course masonry thickness as measures by Petrie. See the reckoning below from Summing Parts.
TheVerticalTunnelSum:
ThePUSH1 ¦ Add1.84
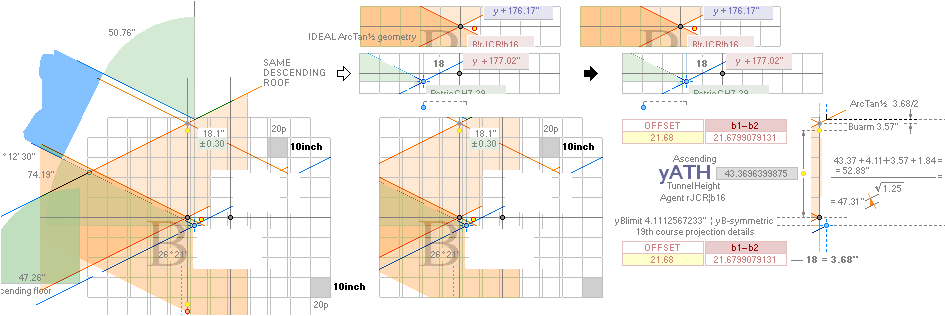
An additional addend ADD1.84 appears through the horizontal
offset between the two sets as bOFFSET — 18 = 3.68’’. Through the ArcTan½
triangle, the y value is half that: 1.84’’. The sum of the parts are then given
below as above.
— SEEN FROM THE composite b-OFFSETED 21.68’’ horizontally
CONTRACTED PETRIE B-POINT (blue): ITS VERTICAL (c) DELIMITS A tunnel vertical
SUMMING OF THE PARTS
c = yATH + yBlimit + BUARM + (bOFFSET — 18)/2.
— And there can be no doubt about that, as seen: Just a
contracted bOFFSET push to
receive a vertical tunnel sum.
— We can test this by quantity in
comparing Petrie’s value for the passage vertical height
— Petrie’s suggested ”19th course projective principle” says that
this height value is the same as the horizontal thickness or height of the 19th
stone block staircase masonry course (at the entrance level) —
as we now anyway have calculated all
the decisive points at the site.
— SUMMING UP THE PARTS as
illustrated we find the vertical roof-floor rJCR¦b16 calculated quantity at the
B-region with the rJCR¦b16 defined Petrie values included, as recently deduced;
— We arrive at the ideal Cheops
Rectangle Golden Section Math ArcTan½ tunnel slope the related sum
c = yATH + yBlimit + BUARM + (bOFFSET — 18)/2 ;
c = 43.37 + 4.11 +3.57 + 1.84 = 52.89’’; paralleling this value
gives the shortest tunnel normal
(52.89)/(1.25)^½ = 47.31’’
(47.3054871141)
If everything fits now, this value
MUST — irrevocably with no tolerance — connect to Petrie’s measured 19th floor
height (668.2’’
± 0.1) as calculated by our EXACT rJCR¦b16 agency values:
— It must define the Petrie given values.
And it SO does.
The results as presented in OpenOffice calCard (conv. spread sheet : what farmers
use for harvesting oats):
Proving he
Petrie 19th floor arithmetics: See also cSIDE illustration
The D-form below is the same as used
in yConBoffset and Add1.84.
ENTER ¦ MainConstruct ¦ SummingParts ¦ ThePush
FOR PREFIXxSIN, SEE TRIGREF unless already familiar.

PREFIXxSIN ¦ R ¦ PetrieCPm

D = 37.9657350065’’ = 19th course
height at entrance:
— And it so does: 37.94’’ ± 0.17 ¦ 47.30’’ .......................... approved
yBarm ILLUSTRATION ¦ TP1Det ¦ SIO
([yATH + yBlimit + Buarm + (bOFFSET — 18)/2]/√1.25)cos(ArcSinR)/cos(ArcTan½ +
ArcSinR) =
37.9657350065’’;
— Descending tunnel: √1.25
transforms vertical to tunnel parallel in the ArcTan½ triangle. 2R = √5 —
1.
:
” The crucial test then is,
supposing the passage prolonged outwards till it intersects this course, how
will its end, and the face of the casing, stand to the casing stones at the
foot of the Pyramid? The answer has been already given in the list of
determinations of the casing angle. It requires an angle of slope of
51° 53' 20"
± 1' ”, PetrieCH6.32.
:
” Mean axis of whole length ¦
Altitude
26° 31' 23"
± 5" ? ”, PetrieCH7.36eTab.
The fact that Petrie used his (idea
of a) casing surface by his staircase masonry measured angle
51° 53' 20" = 51+1/1.125 =
51.8888..° OBVIOUSLY
does not affect the end result
19th course
height 37.97’’ (Petrie 37.96’’¦37.94’’ ±0.17)
on the IDEAL Cheops Rectangle Golden Section paragon Cheops
Pyramid’s (PREFIXxSIN) casing end
angle
ArcSinR =
ArcCot√R = 51° 49’ 38.25’’ = 51.82729238°:
— The construction/paragon OBVIOUSLY includes both.
Quantities approved.
CONCLUSION:
— There seems to be no way in
refuting a general idea that the ideal Cheops Rectangle Golden Section paragon mathematics through the rJCR¦b16 agent in
general DEFINES the whole Cheops Pyramid building — through the Petrie measured
values.
— We find, as of yet, no actual
opposition to that conclusion — still looking for one.
ThePush2: TeP1
PART
II OF THE SEALING PUSH
THE GALLERY ANGLES
THE ACTUAL Pyramid CONSTRUCTED
Petrie measured QUANTITY
In calculating [BUARM] the location of the Petrie
measured [1658.2’’][pGconBuarm]
Gallery PG-point
1658.17’’ = yPG
ArcTan½-math:
......................... (b1 + b1xB)/2 + b1yB — [yBarm = yATH + (BUARM=GSintersectionDiff)]
= 1658.1652607385’’
.............. rJCR¦b16 = b1
through the main ArcTan½ Golden Section paragon geometrical
mathematics,
that ArcTan½ based result WILL
become exactly so certified as
a definite property of the rJCIRCLE agent rJCR¦b16 character:
TP2.1: TeP2
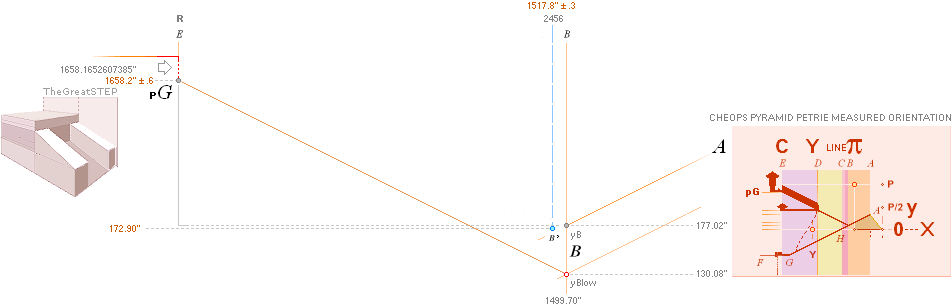
REALIZING THE PUSH to acquire the 21.68’’shorter
Petrie Cheops Pyramid ½ Petrie
measured base
PetrieCP¦b = 4534.4’’ ± 0.25
PetrieCR¦b58 = 4534.20’’ ± 0.000 =
58R√16000 = 4534.196576’’
TP2.2: TeP2
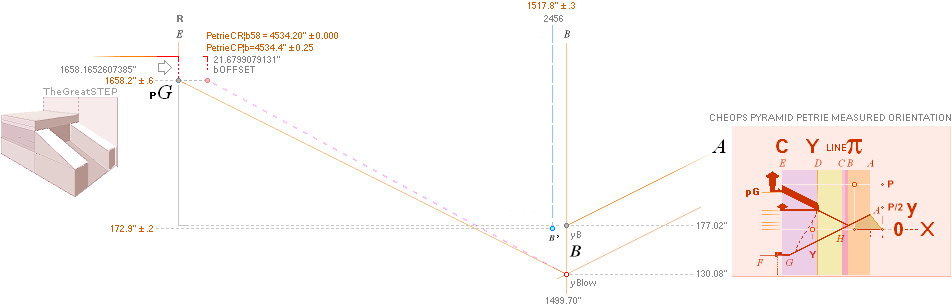
we have arrived at a s(i)t(u)ation
where ANOTHER inner design CONSTRUCT PLAN will be necessary, due to the so
Golden Section paragon rJCR¦b16 breach:
TP2.3: TeP2 ¦ ConAnLi ¦
— The rJCR¦yB point — situated
over the yBlow PG rJCIRCLE agent calculated reference — must now take
a leading constructive position to the layout. Namely on a higher (yB over
yBlow) reference to the former master PG — as »a slave pG».
— This leads the construction plan
into a corresponding basic (absolute) lowest possible ascending floor
construction angle pG→yB of the value 26° 1’ 3’’:
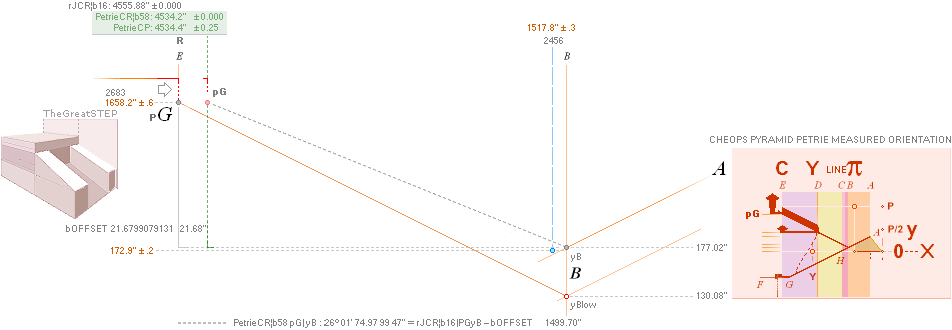
The pG→yB = (minimum)
construction angle for an ascending (B→pG) passage then:
ArcTan(ypG — yB)/(xpG — xB) =
= ArcTan(yPG — yB)/(xPG — xB —
bOFFSET)
=
ArcTan(1658.17—177.02)/(4555.88—1499.70 — 21.68) with calCard rJCR¦b16 decimals
= ArcTan(0.4881106914)
= 26.0174979947°
= 26° 01’ 02.99 27 81’’
Condition:
26° 1’ 3’’ = ConAnLi ........................ absolute lowest floor angle construction limit
— As the real physical Petrie (blue
above) B-point is
vertically y-situated below the master rJCIRCLE Golden Section paragon yB- point
we SHOULD find no smaller measured
values in the corridors and tunnels from Petrie’s expedition on the ascending
slope — in order to keep the construction maximum tight, without »vacillating
around»;
— In Quote PetrieCH7.37 Col3 from Row1 — the angular
values on rows 14¦16¦19¦26¦45¦46.
We will soon return to this specific
part
(proving a reckoning of exact Petrie
corresponding reference angles, further below — with a safe GS body rJCIRCLE
connection).
— First a few GS-observations
on the Petrie mentioned ”plugged part”.
PlugBlockPart: See
Petrie details in The
Measured
The Plugged Part — short
The ”plugged part” (xSouthPP) mentioned
by Petrie, its south end, is directly identified (checked through Petries
values) from the Cheops Rectangle Golden Section paragon situated horizontally
south from the Pyramid’s north base at
xSouthPP = P4 + PiLINE = b·R^[4—1] / √5 + b·R/
√5 ; b=4534.20’’ = rJCR¦b58:
=
(b/√5)(R^3 + R) = 1731.91’’ ;
Length from yB:
—
(xB=1499.70) = 232.21’’
— (Lower offset PetrieCH7.38:
50.76’’)/√1.25 = 45.4’’
= 186.81’’ / 12 = 15.57 feet
horizontally = 4.744974 M.
”.. the large plugs of granite that
fill some 15 feet of its lower part ..”, PetrieCH7.38.
VALUES CALCULATED FROM THE PYRAMID AGENT rJCR¦b16
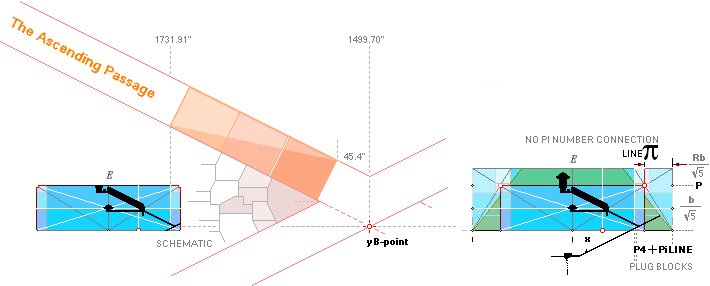
FUNCTION (my reflexion): Without a
HARD (conically shaped, tight fit) plug, the above pushing stone masses would
have shredded the tunnel by time and many small earth quakes. Result from That
Knowing: The Plug was directly added At The Horizontal Construction Site for
stability and minimum stress.
— Additional reflexion: Who made
this geometry? The GS-paragon is a geometrical
structure LIKE Pythagoras Theorem. It has no constructor. It is a natural
property inside geometry: nature stuff — monumented by humans: obviously to
guide later Eventual suck-ups on the right path: Proving an early familiarity. A Monumental Edifice.
— »Occupied by later less educated
suck-ups».
TP2.4: TeP2
Returning (From TP2.3) to The Push:
By consequential constructive
purposes — angle by pG→yB marks the upper limit — the constructing
ascending floor angle slope will hence receive The Petrie B-point B’ as a physical »Lower Floor
BEGINs Here» reference — exactly coherent concordant, as measured by Petrie.
As the Petrie B’ point is xy
situated south drawn below the ordinary rJCR B point by (18.00;4.11)’’, Petrie
will — or should according to our explaining test — measure a slightly greater
angle than the above calculated absolute angle minimum 26° 1’ 3’’:

Namely (exactly)
PetrieCP:
Tan pGB’ = (1658.2 — 172.9)/(4534.4 — 1517.8)
pGB’ = 26.2145061252°
= 26° 12’ 52.22 20 51’’
PetrieCR: With directly Petrie-compatible R-multiples —
where available:
Tan pGB’ = ([2683R]=1658.185192 — [yB’=280R=173.0495169])/(4534.1965759686 — [xB’=2456R=1517.891476])
pGB’ = 26.2142137518°
= 26°12’ 51.16 95 06’’
— PetrieCH7.39:
” This, when corrected for lower
signal being 3 too high, gives
26° 12' 50" for mean angle of both passage and gallery together.
Hence, from my offsets to the places of these signals, the absolute angle, and
the variations from it, can be obtained for either part independently.”
Approved: The values are practically
one and the same.
— I believe this angular line
pG→B’ is what PetrieCH7.45 calls ”the virtual floor”: it is
lying above the actual physical floor as a pure sight-line where the actual
physical floor is being BENT
” which is bent on passing from the
passage to the gallery”
in a (very small) two angle breach at the
beginning of the lower North Grand Galley wall (same level as the tunnel floor
entrance to the Queens Chamber).
— THAT seems definitely VERY
complicated. Is there a rJCIRCLE GS-body connection?
— It better be. We study that
possibility.
TP2.5: TeP2
The Petrie ”virtual” 26° 21’ 50’’ angle will not
do as a final constructed physical floor slope.
— Why is that?
SHORT REPETITION: The PUSH has breached the basic rJCR¦b16
GS-body paragon layout: IT will NOT be found as such inside the corresponding
actual ideal Petrie Cheops Rectangle pyramid PetrieCR¦b58 — unless some
(sophisticated, adopted) adjustment (in the layout) is made.
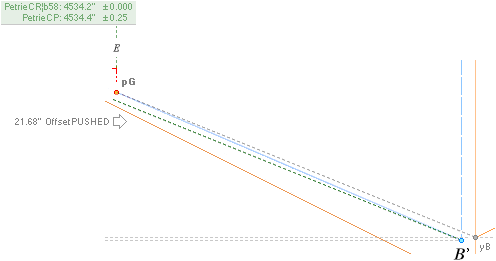
IF our explaining construction plan
is going to hold
— all physically constructed floor
angle parts must lie within the angle sector pG.yB.B’
— then the green lower
parallel to the dotted line pG→yB will mark an absolute physical floor
lower construction limit: it is NOT violated IF our test survives.
— »Petrie shall NOT find an angular
value breaching this condition».
— Where do we find the reference
points for such a highly advanced enterprise?
LATEST MODERN NEWS [Jan2020]:
— »The Egyptian Workers were
psychic, says modern academic archaeological scholars».
— »’They knew exactly where to put
it’, says PhD Walcome Modern to Latest News».
Taking a lead from the original rJCR¦b16 position:
TP2.6: TeP2
— THE SEARCH FOR GALLERY NORTH:
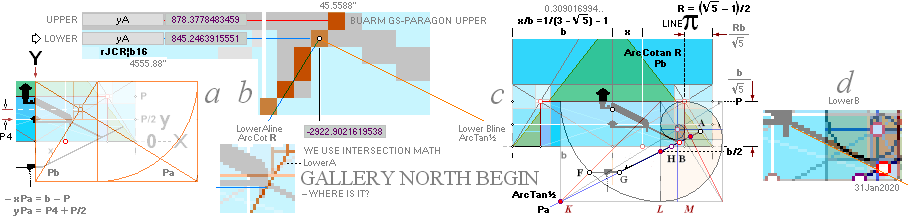
a: The
GS-body paragon used for taking The Aline parameters to the intersecting
point in the LOWER calculated values.
b: Enlarged
view of the Aline on the inner Cheops Pyramid design. The UPPER part — see the BUARM calculation — is not used here in
explicit.
c: The
GS-body paragon used for taking The Bline parameters.
d: Enlarged
view of the Bline on the inner Cheops Pyramid design.
The values above from the (terrible but
free OpenOffice) calCard
expose ”a rough average” to — but
still far from — the Petrie measured corresponding »EXACT» values:
— PetriCH7.39:
”These, added to previous amounts,
give for the absolute place of the floor end at the latitude of the E. wall of
the gallery
(172.9 + 679.7) =
852.6 ± 3 level above
pavement;
(1517.8 + 1389.5) =
2907.3 ± .6 horizontally
from N. edge of Pyramid, or
1626.8 ± .8 northwards from centre;
and 287 ± 1.5 for middle of passage eastward from centre of Pyramid.”.
NOTE: Petrie’s figure ± 3 in ”852.6 ± 3” is — probably, most likely — a
print error:
— In PetriCH7.40tab he writes (here assumed the
more correct ± 0.3)
852.6 ±.3 ¦ Mean doorway on floor
We will take it further on that ±
0.3 part:
By further consequence and (exact)
proof:
— We concentrate only on the LOWER intersection part:
•
At First: We test — certify — that these values, the actual intersecting
point xyA¦B,
![]()
lie OUTSIDE the recently stated
angular limit (TP2.3¦ 26° 1’ 3’’) in the triangle area pG.yB.B’:
— If, namely, the point would be
inside ConAnLi we would have
no reason to continue the search.
— So: How do we do The Test?
— As we already have the xy
coordinates, we (simply) take the xyA¦B point from the Petrie B’ point — our rJCR¦b16 calculated EXACT
construction spouse, of course — which directly gives us a comparing angular
value (absolute xy values only):
Referred [linked sections] values —
all values below in INCHES:
XLoBnom =
LowerBlineNOM ....... = ![]()
XLoAnom =
LowerAlineNOM ...... = b — P
xyAB = intersection point from LineAB, see Intersection Math unless already familiar.
— We directly see that this value
25° 34’ 10’’ is out of hand and range: something (radical) must be done here to
make the construction fit within the (here, still at test) 26° 1’ 3’’ConAnLi preference.
•
At Second: We directly onset the pushing bO = 21.68’’ bOFFSET (TP1¦TP2) to the above nominal rJCR¦b16 values: we
keep these, and just modify them horizontally x-ways with the bOFFSET addition
— plus eventually other near associates (OFK=18 and S=100R are
always close Golden
Section Cheops Rectangle rJCIRCLE candidates);
— We continue (bOFFSET = bO):
![]()
— We still have some work to do
here: 25° 55’ 05 is to short. We must get over 26° 1’ 3’’.
The end result:
The Petrie
D-point: TP26
— This makes it — within Petrie’s
given tolerances:
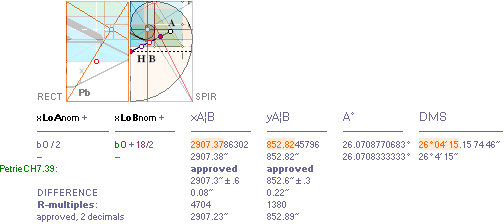
——————————————————————————————————————————————————————————
RECT — SPIR ¦ xLoAnom
¦ xLoBnom ¦ PetrieCH7.39Quote ¦ bO
¦ 18 ¦ R
Defined — as so within the Petrie
specified tolerance limits.
The Golden Section paragon mathematical
geometry truly seems to defend a close connection to The Foundation of a
physical Construction Plan for The Great Cheops Pyramid.
The resulting rJCR¦b16 calculated
angles related to point D is illustrated below in an exaggerated angular
illustration to clarify the details.
TP2.7: TeP2 ¦ OFK ¦ bOFFSET ¦ ConAnLi ¦ yBlimit ¦ pG
EXAGGERATED ANGLES FOR CLARIFYING
DETAILS
The D.B’ angle VIOLET low part DOTTED is truly slightly larger
than the pG-B angle GREY DOTTED: The Violet 26° 3’ should have
been positioned between the gray 26° 1’ and the blue 26° 12’.
However to give a view on the D-point, an illustrative violation is made here
in pushing D outside the allowed, making us »a split vision geometrical view» of the whole complex.
The values below are the true angular values as calculated in the following
tables. The top VIOLET Gallery part parallel to D.B’ will be
discussed further [‡],
included here only for reference.
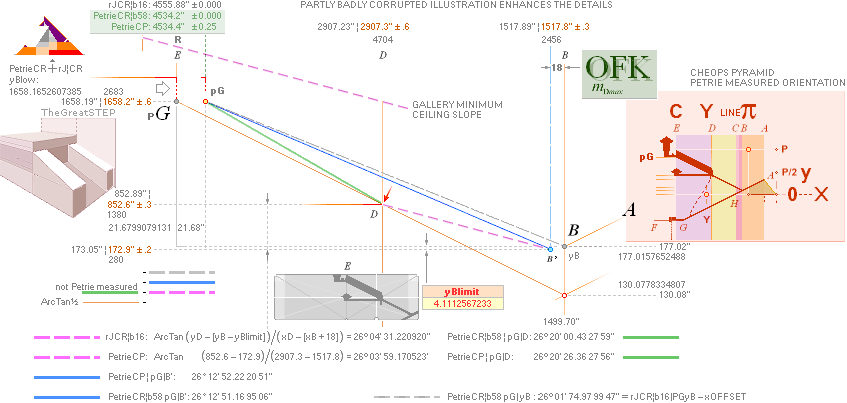
The R-designation on top [and
associated] row gives the corresponding Within-Petrie-Tolerance whole number
R-multiple [WRM], if at all,
2 decimal rounded. The Petrie D-point xy coordinates
as calculated and Petrie given:
PDang: TP27
The compiled calCard calculated
angular values associated with Petrie’s D-point:

TheLostAngle: PDang
Petrie’s
”signal to signal” In Quote Row30 PetrieCH7.39.
”Signal” — 1883? Not with any Transistors anyway.
Measuring (solid, geodesic, trigonometric, theodolitic) reference
points.
— The only known TRIGONOMETRIC way
to understand Petrie’s description In Quote Row30 PetrieCH7.39 is (TP27) as seen from the Petrie D-point:
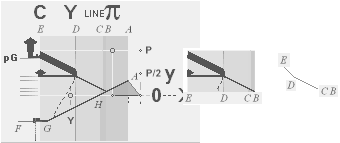
The distance E.(CB) or its end
angles can be calculated
only if the distances D.(CB) and D.E
are known together with their respectively angles.
— However, apart from the quoted
PetrieSignal section:
— Petrie gives no (direct)
information on WHERE his ”signal” were situated, especially at the south
Gallery end — except In Quote Col1 ¦ Row26 PetrieCH7.46 the additional
information in PetrieGallery.
— PetrieCH7.39 ¦ Col2 ¦ Row11: ”the sloping
length of the passage being 1546.8’’.
SPECIAL TRIGONOMETRIC TRIANGULAR
CONNECTIONS:
In PREFIXxSIN: b = E→B = (ac[a/c + c/a — 2sinF])^½
:
c = D→B 1546.8’’ ”from beginning of ascending passage”
(D.B)° 26° 2' 30" In Quote PetrieCH7.38 Col3 Row14
a = D→E 1815.5’’
In Quote PetrieCH7.45 Col2 Row13
(D.E)° not connected, missing data
b = E→B cannot be calculated without a
(D.E)°
(E.B)° cannot be calculated without a
(D.E)°
F° = 180° — (D.E)° + (D.B)°
THAT IS TO SAY:
No angular value
— only a distance value ”Ramp end 1815.5”
— is mentioned between the reference
points D and E (pG)
— ”.. but we can obtain the angle of
slope very satisfactorily, by taking the
angles observed to signal at bottom of ascending [p. 65] passage, and to signal
at top of gallery, and then (knowing the distances of these signals)
calculate the angle of slope from signal to signal”, PetrieSignal Row25.
From where did Petrie get a (D.E)°
value?
— He mentions no value.
What (D.E)° angle?
We can test this precisely with our rJCR¦b16
exact mathematical GS-body geometry in comparing the other Petrie given values
on the lower Gallery part (Petrie D point) of »The Petrie Queen Site
expedition»:
— As is evidently shown in the Petrie D point section, the
acquired corresponding rJCIRCLE complex values lie within the Petrie given
tolerances:
Not mentioned by Petrie, only suggested:
PetrieCH7
accounts for »a general method» in calculating the mean Gallery floor slope
from known angles and lengths by his ”signal to signal” (In Quote PetrieCH7.39 Row30).
PetrieCH7.38 In Quote Col2 Row11 specifies length
D→B’= 1546.8 on angle 26° 2' 30" In Quote PetrieCH7.38 Col3 Row14:
”.. The angle of the whole passage will be
discussed further on; it will suffice to say here that the mean angle is 26° 2'
30"; and there is therefore a presumption that the plugged part is about
the same angle”.
— PetrieCH7.45tab In Quote Col2 Row14 specifies a ”Ramp end ¦ Distance on slope
1815.5” as (crosscheck by trigonometric calc.) Length D→pG¦E.
But Petrie gives
no actual angular value
(calculated PDang as above 26° 20’ 26.36 27 56’’)
for this length
D→pG
(neither a value of ” 20’ ” exists in the text, and
nor any ”19’ ” — A lowest Petrie 1658.2±0.6=1657.6 gives a 26° 19’
.. But neither such a figure is mentioned in Petrie’s text;
— As we, here, rely on this indirect Petrie 1658 figure, we really have no
detailed clue in how Petrie reached his top slope gallery step face level value
as mentioned
In Quote PetrieCH7.46
Col1 Row40, the figure
1689.0 ± 0.5 [with an explained additional measured + 4.16 = (1693.16 ±
0.6 → nom1693.2)]).
xy-difference:
±0.6’’¦0.08’’; ± 0.3’’¦0.22’’
PetrieCH7.39 values: responding rJ calculated:
xD = 2907.3’’ ± 0.6 2907.38’’ ¦ 2907.3786302
yD = 852.6’’ ±
0.3 852.82’’ ¦ 852.8245796
———————————————————————————————————————————————————————
”These, added to previous amounts,
give for the absolute place of the floor end at the latitude of the E. wall of
the gallery
(172.9 + 679.7) =
852.6 ± 3 level above pavement;
(1517.8 + 1389.5) =
2907.3 ± .6 horizontally from N.
edge of Pyramid, or
1626.8 ± .8 northwards from centre;
and
287 ± 1.5 for middle of passage
eastward from centre of Pyramid.”, PetrieCH7.39.
———————————————————————————————————————————————————————
:
— The D.E
angle with nominal values from Petrie1658:
Tan(D.E)° =
(yPG—yD)/([xPG=bPetrie=4534.4]—xD)
(D.E)° = ARCTAN (1658.2 — 852.6)/(4534.4 — 2907.3)
= 26.3406563211° = 26°
20’ 26.36 27 56’’
— The
trigonometric formula for the Petrie reasoning ”signal to signal” method,
demands (2
sides, 1 summing angle: from reference point D)
knowledge of
both lengths:
— The downwards
descending
c = D→B’
= 1546.8’’ and the
PetrieCH7.45tab upwards ascending
a =
D→pG¦E = 1815.5’’ and their angles
F° = 180°
— Upper° =
26.3406563211 = 26° 20’ 26.36 27 56’’
...... our HelpPetrie
missing calculated DEangle.
+ Lower° =
26.0416666666 = 26° 02’ 30.00 00 00’’ ....... Petrie’s
nominal In
Quote PetrieCH7.38 Col3 Row14
= 179.701°
PetrieBE: FourGiven ¦ DEangle ¦ The Lost Angle
THEN WITH a GIVEN — COMPLETING THE
PETRIE MISSING INFO — WE CAN FINISH ON WHAT PETRIE MUST HAVE COMPLETED: THE b
SIDE FROM acF°, AND THEN FINALLY THE yPG FROM THE PYTHAGOREAN FORM WITH b AND
xyB.
Most simple (we
calculate distance b = pG→B’ from The four given):

In PREFIXxSIN:
b = pG→B’
= (ac[a/c + c/a — 2sinF])^½ =
=
3362.2886273723’’. The b-angle: ArcSine (4534.4-1517.8)/b =
b° =
26.2093239122° = 26° 12’ 33.56 60 84’’
(Petrie’s 26° 12½’ angle in CH7.38 ”.. and
26° 12½ ' as the ascending angle”).
The horizontally
b-projected length (b·sinb°):
xb = 3016.6’’ ............ PetrieCH7.64tab results also specifies 4534.4—1517.8=3016.6
[Table error 3016.3];
compared to the
alternative Petrie given (½Pyramidbase=4534.4) — (xB=1517.8) =
xb = 3016.6’’ —
Same value.
PetrieIndirectlyVerified1658:
STRONGLY EXAGGERATED ANGLES FOR CLARITY — PetrieBE
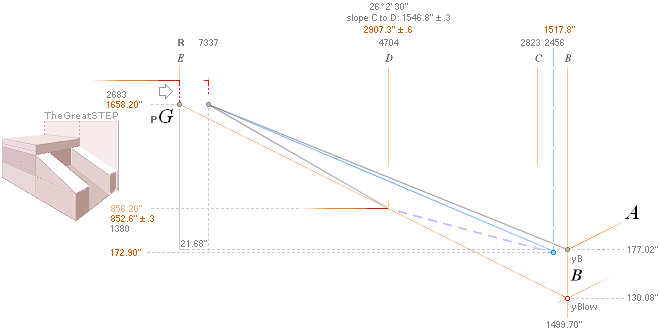
The resulting vertical pG-point
height from the trig-form:
 The Pythagorean form with recent
designations:
The Pythagorean form with recent
designations:
√[(b=3362.2886273723)² — [(½PetrieCheopsPyramidBaseb=4534.4)
— (xBPetrie=1517.8)]²]
+ (yBPetrie=172.9) =
ypG =
1657.8610276897’’ ~ 1657.86 compared to (the indirectly Petrie1658 summed)
yPG = 1658.2’’
± 0.6, lowest 1657.6. Nominal
Difference: 1658.2—1657.86 = 0.34.
— Approved and
verified.
These Petrie cross checking tested
calculations (initially and necessarily [perhaps] made by Petrie from 1883)
only confirm the correspondences on the Petrie (indirectly calculated) Gallery
top sloping floor pG-point — however never explicitly mentioned by Petrie
himself. See QuotePetri1658.
We see — for comparing clarity —
that the Petrie given nominal values have small (discernible) deviating figures
from other slight different numbers WITHIN the Petrie given tolerances. The PDang calCARD above exposes this explicitly on
the first top row, same within-tolerance figures: Petrie’s part at the right
and the rJCR¦b16 calculated to the left, same (Petrie tolerance) approved D
point.
PetrieDAngles:
TP27
Petrie on the D-associated angles
26° (2-7)’¦26° 12’¦26° 20’
— See In Quote Col3 PetrieCH7.38.
— See also The Petrie Signal Section PetrieCH7.39:
— See also The Plugged Part.
— Petrie mentions the D-point
associated angular uncertainty part in
PetrieCH7.37:
” The surfaces are so much decayed and
exfoliated, that it is only just at the ends that two original faces can be
found opposite to one another; hence the width and height cannot be measured,
and the offsets can only be stated to one surface.
From this altitude, the sloping
length of the passage being
1546.8, the horizontal length will
be
1389.5, and the vertical height
679.7, both being corrected for
difference in the offsets of the ends.
The determination of the azimuth
has, unhappily, a large probable error,
± 3' (owing to bad
foundation for the theodolite in Mamun's Hole); and its direction,
– 4', is so close
to that of the Pyramid side, that it may be assumed parallel to that
± 3'. This, on the
passage length, =
1.2 inches for the probable error of
the place of the upper end of the passage, in E. to W. direction in the
Pyramid.”.
Calculating example from Petrie’s
values — showing the relative errors:
ArcSin(1389.5/1546.8) =
............... 26° 3’ 49.29’’
ArcCos(679.7/1546.8) =
................ 26° 4’ 1.53’’
ArcTan(679.7/1389.5) =
............... 26° 3’ 59.17’’
These values compared with the
previous, top row
Petrie CP¦DB’: .......
ARCTAN (852.6 - 172.9)/(2907.3 -
1517.8) =
= 26°
3’ 59.17 05 23’’ ←
b16compar.: ..........
ARCTAN (852.8245796 — [177.0157652488 — 4.1112567233])/(2907.3786302 — [1499.7016293661 + 18] =
= 26°
4’ 15.15 74 46’’
show that ”the exact” internal
Petrie preference here is of the TANGENT type — same DMS (DegreesMinutesSeconds)
figures — While the ArcCos-part is more close to the rJCR¦b16 calculated part.
— In any of the ways, we see that
these Petrie given METRIC figures lie within his given tolerances.
So:
— Any of these values will find an
approved recognition.
The corresponding PetrieCR¦b58 has
no known match
An interesting parallel:
— What (corresponding) values are
given by the PetrieCR¦b58 part?
— Not good: The RECT(type:—5.85) and
SPIR(Type:+24.7)
have to be pushed in opposite horizontal directions for a corresponding Petrie
approving near xyD 2907.36; 852.76. That is obviously, as we know, not our
table: no known correspondence. It is all about the rJCIRCLE part.
— Calling ATLANTIS .. ello .. ello .. 222 ..
333 .. ¦ ATLANTIS ¦ GTursprunget2019 ¦ AtlantisAPPENDIX ¦
— Roger .. Roger .. Mayday .. Mayday .. A GEOATLANTIS seems to be
capable in EXPLAINING else-way enigmatic GLACIATION VARIATIONS — reported only
over the NORTHERN HEMISPHERE.
DESCENDING PASSAGE
LowHighMEAN:
Finding
the most direct and simple adopted exact quantities from the Golden Section
paragon mathematical geometry
DESCENDING PASSAGE LowHighMEAN
by rJCR¦b16 = 4555.88’’
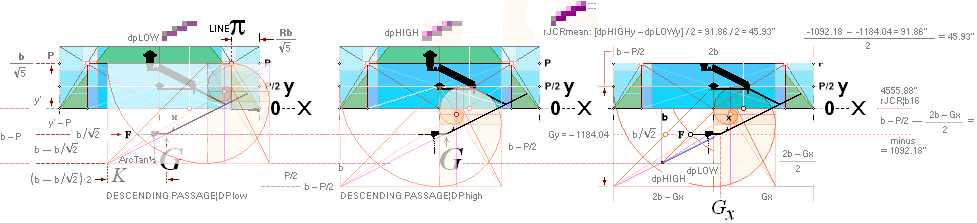
The Descending Passage DP vertical
height
— testing quantity matches to the
1883 Flinders Petrie Cheops Pyramid measurements
We have two independent ways leading
to the same result.
— The illustration’s left part shows
the two most obvious visual fittings for the GS-body on the Petrie measured
inner design of the Cheops Pyramid. We see (by magnification, see on top) that
the leftmost dpLOW candidate exposes a slight lower paragon fit than the middle
dpHIGH one.
— Allowing only use of the GS-body’s
definite geometrical quantities the above illustrated math conditions appear:
— The difference in vertical height
between dpLOW¦y and dpHIGH¦y becomes
—(b — P/2 — (2b — Gx)/2) + Gy = |1184.04|’’
— |1092.18|’’ =
91.86’’ with rJCR¦b16
= 4555.88’’ ;
The mean vertical (y) difference
between the the two is
(dpHIGH — dpLOW)/2 = [—1092.18’’ +
1184.04’’ = 91.86’’]/2 =
45.93’’
See also general drawing metrics and
calculated results more in detail in
With respect to the actual construct
(Petrie mentions ”a flat end”) at the end of the tunnel, Petrie gives two
values:
PetrieCH7.37tab.
upper edge ............ 48.5’’
lower edge ............. 38.3’’
Extracted @Internet SEE The PETRIE SOURCE for research
purpose
— testing Petrie measured values
against the GS-body
mathematical geometric quantities: PROVING THE CONSTRUCT.
Comparing the Petrie
values with the averages rJC¦CR-values have no visible representation to the
naked eye in this illustrated scale (from PetriePLATE.9).
For the local
rJCR-values, see Phase1RESULTpointG.
WHOLE NUMBER R-multiples can
be tested with Petrie’s given values and their tolerances — as it now already
is clear (Background ¦ IntroEX) that the
construct DID use such GS-paragon precision methods (and
instrumentation).
EXAMPLES with multiple R
— confirmed by
Petrie measured values
Directly with S = 100R = 61.80’’:
S(7 + 1/100) = Kings
Chamber Ceiling Midpoint from Pyramid vertical Centre:
433.24’’ = 433.2418261 = 701R;
— PetrieCH7.55e:
” The position of
the King's Chamber in the Pyramid is defined thus:
N. wall at base
330.6 ± .8 S.
of centre of Pyramid; S. wall
537.0 ± .8 from
centre; .. ”
Check: (N¦330.6 + S¦537.0)/2 =
433.8 ± 0.8 ¦Low¦433.0;
Hih¦434.6 ................... approved
NomDiff: 0.558.
All the following Petrie given
measuring series on the so called Queens Chamber have whole R-multiple quantities within the
Petrie given tolerances:
QUEEN CHAMBER
PetrieCH7.40tab: ¦Floor level¦Theodolite
measured ¦ R = (5^½ — 1)/2 = 0.618033998..
— The whole Petrie series of values
approve:
OPEN OFFICE CalCARD.

The OK cell code: IF Difference
>Tolerance THEN print ”notOK” else print ”OK”. OK means: approved.
NoProblemo.
These value
examples MAY seem »a little trivial»: The R-unit — R = (5^½ — 1)/2 =
0.681033988.. — is pretty much ”precisely” ± 0.3. On the other hand: »The
Constructors counted on precisely that».
— Without speculation
— speculative conclusions are not allowed here — we can neither prove nor
refute these possibilities. It fits (any way).
Specifically we
have the (vertically) Queen’s (partial) floor level
y = 1385·R = 855.9770744;
yQUEEN = 855.98’’ ¦ Petrie 856.2
±.3 ¦On floor ...................... APPROVED
NomDiff: 0.222.
with the
corresponding horizontally Petrie measured connecting point between the end of
the Ascending passage — where it meets the beginning of the Grand Gallery, and
the horizontal tunnel into the so called Queens Chamber, PetrieCH7.39:
” ..
(1517.8 +
1389.5) =
2907.3 ± .6 horizontally from N. edge of
Pyramid, or
1626.8 ± .8 northwards
from centre; and 287 ± 1.5 for middle of passage eastward from centre of
Pyramid.”
x = 4704 R = 2907.231883 ~
2907.23’’ ¦ ........................................................................................... APPROVED
NomDiff: 0.002.
And further.
— Calling ATLANTIS .. ello .. ello
.. 111 ..
333
— Roger .. Roger .. Mayday .. Mayday ..
CONCLUSIONS: What18: — OFK OFFSET FACTOR K ¦ The ±e-mass quantity
responsible for all atomic masses as defined in TNED ¦ — Compiled
for UD Jan2020 —
WHAT 18? See also in The MiUNIT.
— As
already noted: Not much in this presentation is known in modern academic
quarters.
Construction
basics as proved
FLOOR
19 AND ROOF 18 ¦ Proving the 19th Floor — rJCIRCLE complex connection to Cheops Pyramid
— All
most essentially and universally connected to ELEMENTARY atomic and
nuclear physics.
— See
WHAT18 a (shorter) detailed description in
(CheopsAtlantisTNED), unless WHAT18 already familiar.
MiUnitIntro:
THE CHEOPS UNIT S = 100R
MiUNITbasic ¦ The MiUNIT ¦ MiUNIITcomparingTable
The MiUNIT — INTRODUCTION, How it was observed
[Nov2017], see KingILLUSTRATION.
— The Pyramid half square Base (b)
multiplied in succession by the Golden
Section Constant R = (5^½ — 1)/2
as in b·R^n with n from 0 and up
gives — with rounded two decimals — on n=18 the value 1.27 — which is 2.54/2.
— See these values in Table @ExactComparingBasics.
— We can use Petrie’s Cheops Pyramid
[CP] measure
PetrieCP¦b = 4 534.40'' or the ideal 2 decimal
ROUNDED Petrie Cheops Rectangle [CR]
PetrieCR¦b58 = 4534.20'' or the full decimal
PetrieCR¦b58 = 4534.196576 = 58R(16000)^½.
— All end on n=18 at 1.27.
— And there we go: The GS-body
arithmetics contains a (Pyramid measuring basic) MeterInchUNIT of the form
0.0254 M = [ROUND 100·(2b·[1Meter/1Inch]/R)·R^18]/10000
=
1'' ;
2.54 =
2b/R · R^18
bReferences:
The 2 pyramid b-agents
¦ GS arithmetics
See also the [b¦PnMAP] (Sw.orig.2017)
bPetrieCheopsTable.
— The corresponding ideal GS-body
geometrically EXACT PetrieCR¦b58 spouse 4534.20 tabled values are shown (here
recalculated Jan2020) below:
— The Pyramid
half square Base (b) multiplied successively by
R = (5^½ — 1)/2
as in b·R^n with n from 0 and up gives
— with rounded
two decimals — on n=18 the value
1.27 — which is
2.54/2.
— We can use
Petrie’s Cheops Pyramid measure
PetrieCP¦b =4 534.40'' or the ideal 2
decimal ROUNDED Petrie Cheops Rectangle
PetrieCR¦b58r = 4534.20'' or the full decimal
PetrieCR¦b58d = 4534.196576 = 58R(16000)^½.
— All end on
the same n=18 @1.27.
— And
what’s so special about 18? The Neutron — the rJCircle BASE. The
whole complex — says TNED. »Central
Nuclear number»:
— The Atomic Masses certifying that TNED + Experimental physics = True. THE NEUTRON SQUARE — unknown in MAC.
ExactComparingBasics, the MiUNIT:
Table extracted and recalculated and
compiled here for comparing values from the original Swedish version 2017.
— ABBREVIATIONS and terms are
detailed in HowStart — unless
already familiar.
— All end on
the same n=18 @1.27 = 2.54/2:
— We have found
a (Pyramid measuring basic) MeterInchUNIT of the form
0.0254 M = [ROUND 100(
2b[1Meter/1Inch]/R)R^18]/10000
= 1''
1 Inch = 0.0254 Meter —
standard electronics construction raster [10UNIT] for integrated circuits.
Really.
— NOTE: 5·8 +
18 = 58. Really (»Advanced
Alzheimers»). See The
1818+18+k Neutron.
— The Mi¦UNIT. The PETRIE¦Cheops Pyramid
Unit [»The CU»]. Petrie and his working group — and the
contributors who showed the parts — are responsible for this discovery (with
some supporting interest from an accidentally passing by pedestrian ..).
The MiUNIT: MiUNITbasic ¦ FIRST APPEARANCE
COMPARE
PetriCP and PetrieCR
The Mi¦UNIT — MeterInchUNIT ¦ 16 •18 • 58
R = Golden Section
Constant (5^½ — 1)/2 = 0.618033988..¦ b, see bREFERENCES — Cheops Pyramid ¦ k0
With Petrie’s specified measure 61.7±0.8 inches from
the Pyramid Centre (C-line), we can most freely with only a utilized tolerance
of ± 0.15 adopt a (MeterInch-UNIT) in association with the 100R =
61.80’’ Petrie Cheops Pyramid Top Gallery value through the following exact
corresponding arithmetics:
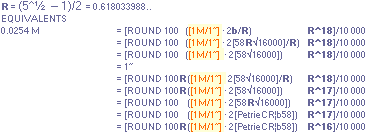
Petrie100Rsource: MiUNIT
PetrieCH7 mentions the
61.7 (± .8) value 5 times. We have
61.8 = 100R:
The Golden Section body Relational
value
R = (5^½ — 1)/2 = 0.618033998.. has
several direct WHOLE NUMBER R multiple quantitatively affirmed connections to
the 1883 Flinders Petrie given Cheops Pyramid measured values — WITHIN Petrie’s
specified tolerances.
Directly with S = 100R = 61.80’’ = CheopsPyramid UNIT
(CPunit):
S(7 + 1/100) = Kings
Chamber Ceiling Midpoint from Pyramid vertical Centre:
433.24’’;
— PetrieCH7.55e:
” The position of the King's Chamber
in the Pyramid is defined thus:
N. wall at base
330.6 ± .8 S. of centre of Pyramid;
S. wall
537.0 ± .8 from centre; .. ”
Check: (N¦330.6 + S¦537.0)/2 = 433.8
± 0.8 ¦Low¦433.0; Hih¦434.6 ............. approved
See also THE QUEEN’s SERIES:
All Petrie given measuring values on
the so called Queens Chamber
PetrieCH7.40tab: ¦Floor
level¦Theodolite measured ¦
have whole R-multiple quantities within the
Petrie given tolerances.
k0: SPECIFIC CHEOPS
RECTANGLE RELATION — rJCIRCLE radius to half Pyramid Base
From
the Swedish Edition original kCHEOPS
RELATION
BETWEEN THE CHEOPS RECTANGLE GOLDEN SECTION ENVELOPING CIRCLE RADIUS rJ AND HALF PYRAMID BASE
b
With a given rJ quantity, the
corresponding b value is given through
b = rJ/k0
See also the introduction in THE TWO PYRAMID AGENTS.
THE LINE INTERSECTING CONNECTION
CROSS
COORDINATES FOR TWO STRAIGHT LINES ON A GEOMETRICAL PLANE
LINE
INTERSECTION
GIVEN:
Two
straight lines LINEa¦xy and LINEb¦xy with Angles AB:
y-intercept:
LINE
INTERCEPT (N) on y-axis:
y(N)
= y — tanLINJE · x ...... actual line
lines
intersect at point
INTERSECTION
LINES¦ab:
xP =
(Nb — Na)/(tanA — tanB)
yP =
Na + tanA · xP
---------------------------------------
COMPARING
VERTICAL DIFFERENCES BETWEEN TWO PARALLELS:
VertDiff
= |Na — Nb|
— Calling
ATLANTIS .. ello .. ello .. 111 .. 222

— Roger .. Roger .. Mayday .. Mayday ..
ArcTan½GSline: GS-body
THE
DIFFERENT INTERNAL DESIGNATIONS IN THE GS-BODY PARAGON IS EXPLAINED MORE IN
DETAIL IN the GS-BODY
THE ArcTan½ LINE IN THE GS BODY
— How
the central ArcTan½ line inside the GS-body paragon structure can be deduced is
shown below.
PiLINE:
PLUG BLOCKS ¦ Pn bn R ¦ Note: THE xPiLINE=PR — definite geometrical
quantity — has no connection to the PI number, as as we know:
piLINE has no pi number connection
— The Pi number
3.1415.. is a so called TRANSCENDENTAL number: it has no definite
geometrical measure;
— The Circle’s perimeter 2·pi·r is
»open» or »undefined» through unlimited
arithmetical series:
pi/4 = 1 — 1/3 + 1/5 — 1/7 + 1/9 —
... = 0.785 398 163 .. The summation in this form converges extremely slow.
The
ArcTan½ line in the GS-body:
R =
(√5 – 1)/2
= 0.618033988..
= 2/(√5 + 1) =
1/[1 + (√5 – 1)/2] = 1/(1 + R); 1
+ R = 1/R ; R
= 1/R – 1 ;
1 – R
= 1 – (1/R – 1) = 2 – 1/R ;
(1/R)2 = 12 + R2 + 2R = 1 + R(R + 1 + 1
= 1/R + 1) = 1 + 1 + R = 2 + R ;
1/R2 – R = 2 ;
b2/(d – b3)
= b · R / [b/R
– bR2] = R/(1/R – R2)
= 1/(1/R2 – R)
= 1/2 ;
The hABb triangular
formula ![]() is often used IN MATHEMATICAL GEOMETRY
ANALYSIS for checking, receiving and comparing values.
is often used IN MATHEMATICAL GEOMETRY
ANALYSIS for checking, receiving and comparing values.
End GALLERY SOURCES: MiUNIT
SOUTH END
GALLERY SOURCES:
1658.20’’ ±
0.60 ...... See quotes in PETRIEpG:
Petrie does not
give the direct pGallery value 1658.20’’ ± 0.6, only its two components at The
Great Step up at the end of the so called Gallery part:
PetrieCH7.46:
”.. the height
of the step face is 34.92 or 35 on E. ..”
”.. the step surface at the E. side of the S. doorway is 1693.2 ± .6 over
the pavement.”;
— We calculate
the difference as
1693.2 — 35 =
1658.2 (± 0.6)
339’’
.......................... Petrie given
data in PetrieCH7.46s2¦5:
” The roof of
the gallery and its walls are not well known, owing to the difficulty of
reaching them.”
” .. therefore
at half the height of the gallery, that varying from 167 to 172.” : 167 + 172 = 339.
— Wikipedia
Great Pyramid Nov2017 specifies a Gallery height ”8.6 metres (28ft) high”:
338.58’’ resp. 336.0’’. In the first case we see a fair correspondence to the
(uncertain) Petrie values 167+172=339’’. No other data sources on the subject
are known here;
339’’ = 8.6106
M.
The MiUNIT —
61.80’’, 2 decimal rounded from 100R:
61.7’’ ± 0.8
............ Petrie given data in
PetrieCH7.45e, here taken nominally fixed as 100R = 61.80’’.
PetrieCH7.45e:
” Hence the floor of the galley intersects
the S. wall at 1689.0 ± .5 above the pavement; at 61.7 ±.8 S. of the pyramid
centre”; CH7.64tab.: ”61.7 ± .9”;
PetrieCH7.46e:
” And as the virtual floor end is at 1689.0
± .5, the step surface at E. side of the S.
doorway is 1693.2 ± .6 over the pavement.”; CH7,47tab.: ”1693.2”.
NOTE — PetrieCH7.46s2 certified Gallery uncertainties:
As Petrie (and others) already has pointed
out, partly cited as above:
— No (more) scrutinized measuring
investigations have been made (as known here Dec2019) on the Gallery roof.
The partly averaged figure (339’’) in the result above hence has a
certain quality of NOT being definitely settled by direct measures.
More precise quantities are needed to confirm any definite here
associated South Gallery Roof top fit
as included in
Petrie’s own commented ”difficulty of reaching” the details.
PetrieCH6.24:
PYRAMID STAIRCASE MASONRY SLOPING ANGLE
See PetrieSOURCE.
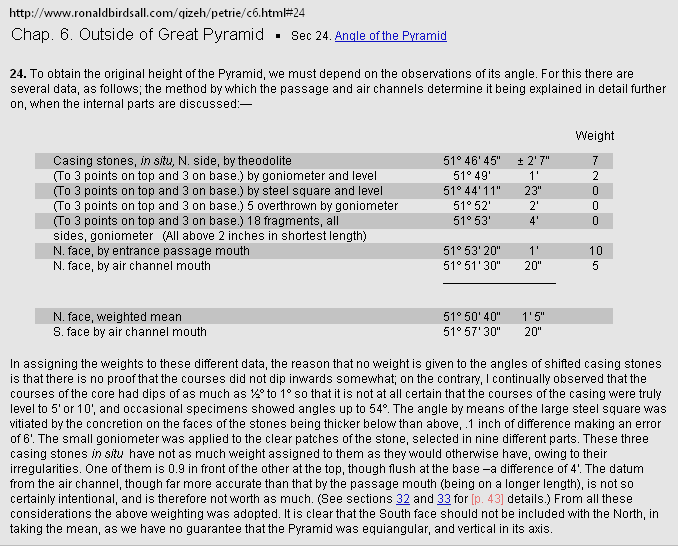
PetrieCH6.25: See PetrieSOURCE.
”On the whole,
we probably cannot do better than take 51° 52' ± 2' as the nearest
approximation to the mean angle of the Pyramid, allowing some weight to the
South side.
The mean base
being 9068.8 ± .5 inches, this yields a height of 5776.0 ± 7.0 inches.”.
PETRIEb = (9068.8±0.5)’’/2 = (4534.40±0.25)’’;
Lowest: 4534.15 = 4534.40 —
0.25; (—6.35mM)
Highest: 4534.65 = 4534.40 + 0.25; (+6.35mM)
The mean 51° 52' is given directly
from Petrie’s two pyramid staircase masonry slope values on the North face of
the Cheops pyramid by
[(51° 53’ 20’’) + (51° 51’ 30’’)] /
2 = 51° 52’ 25’’.
The direct Petrie
theodolite/goniometric measure on the actual remaining casing stones gives at
least one precise agreement (51° 49’) with the ideal Cheops Rectangle (Golden
Section) angle,
ArcTan (h/b =
1/√[R=(—1+√5)/2]) = 51.82 729 237 ° = 51° 49’ 35.2525’’.
Neither Petri, nor others (searched
for, not found) gives a specific description of exactly WHERE in the outside
remnants of the Cheops Pyramid the remaining (”few”) casing stone blocks
actually are situated. A complementary collection of photos from Internet show
similar site views of these few remaining original covering blocks. See IntroTEF. Petrie gives
us (only)
PetrieCH6.29:
See PetrieSOURCE.
”Now the remaining casing stones on the N. base ..”.
We should not suggest
(PetrieCH6.24, ”To obtain the original height of the pyramid”)
that Petrie with his pyramid
staircase masonry average slope 51° 52’ intended to state or establish an idea
of ”the original pyramid casing slope”. At least not as I know.
— Petrie just
refers a measured average on the site with specified premises.
Here, no other information of the actual
Cheops Pyramid remnants is known.
”The mean base being 9068.8 ± .5
inches, this yields a height of 5776.0 ± 7.0 inches.”
As the information from Petrie is
understood and apprehended here:
— Petrie calculates the height
(5776’’) of the building from the pavement floor by the tangent averaged slope
value 51° 52’, together with the measured base value (4534,40’’). This suggests
the idea of an ideal pyramid height with an ideal original flat casing surface
as seen from the base front casing stone edge.
Not from the actually more narrow
core Petrie based measured staircase masonry.
— We would have
expected Petrie to clarify this part by stating that his (51° 52’) casing idea
is that of the measured remnants of the STAIRCASE masonry — and nothing else.
But, as far as it is known here, Petrie does not give that type of elucidation.
On the other hand, Petrie gives the angular tolerance ± 2’, lowest 51° 50’,
which is (very) close to our ideal Cheops Rectangle bd=h² pyramid angle C° =
51° 49’ 38.25’’.
— As Petrie states above, ”owing to
their irregularities”, the actual remaining casing stones at the base (the
Petrie 51° 49’ casing stone
measure) have less certainty weight than the long staircase walls.
Petrie specifically refers to a
(possible) final pyramid height (but assures its estimate is inadequate) in
PetrieCH6.23:
See PetrieSOURCE.
” These levels, though important for
the heights of the particular courses,
have scarcely any bearing on the
question of the original peak of the casing
of the pyramid,
because we have no certain knowledge of the thickness of the casing on the
upper parts.”.
PetrieQuotes:
See PETRIE SOURCE
Col1 ................ PetrieCH7.46
.............. Col1 ................ Petrie Gallery
Col2 ................ PetrieCH7.45
.............. Col2 ................ Petrie Signal 1546 ...... row11
Col3 ................ PetrieCH7.38
.............. Col3 ................ Petrie Signal 2621 ...... row46 ............. PetrieSignal 230 ......... row14

The Crucial
................. row43
Petrie StationMark
..... row53
Petrie Hangle
............. row51
¦ 55

THE PYRAMIDS
AND TEMPLES OF GIZEH, William Flinders Petrie 1883
W. M. Flinders Petrie
1883 — @INTERNET Ronald Birdsall, 2003-14
PetrieCH7.39
.............. PetrieSignal

PetrieCH7.46 .......... Petrie
Gallery Roof Top

PetrieSource:
PetrieQuotes ONLY IN
RELATED PARTS
THE
PYRAMIDS AND TEMPLES OF GIZEH, William Flinders Petrie 1883
W. M. Flinders Petrie 1883 — @INTERNET Ronald Birdsall, 2003-14
http://www.ronaldbirdsall.com/gizeh/petrie/index.htm
TYPOGRAPHICAL
NOTE — original @Internet Petrie text — denotation for degrees:
Character
Alt+0186 shows ° º while Alt+0176
shows ° °; enlarged right.
— Some of the Font
Types does not show the difference in smaller font sizes.
— The above
quoted is directly copied from the Internet source — where it looks like a
raised small ring — in Windows Note Pad: IT obviously »Develops Feet» and takes
another form in another hotel.
— Here all
angular quotes from Petrie’s Internet source text have been adopted to the
simple ring form, assuming the original purpose was such.
The 19th
COURSE Floor: Proving the 19th
THE 19th FLOOR — 668.20’’ ± 0.10
SEE
SPECIALLY APPENDED SECTION IN How Petrie Reckoned the Entrance
Geometry
— Here we refer the decisive Petrie
presented values.
TEXT AND IMAGE SOURCES, see PetrieSOURCE.
” 35. [p. 55]
Having, then, fixed the original position of the doorway of the Pyramid, we may
state that it was at
668.2 ± .1 above the pavement of the Pyramid;
524.1 ± .3
horizontally inside (or S. of) the N. edge of the Pyramid casing; and its
middle
287.0 ± .8 E.
of the centre1 of the Pyramid; or
3723.6 from E.
side, and
4297.6 from W.
side, at its level; the probable error being that of fixing the length of the
sides. Thus we have the following positions in the entrance passage, reducing
all to the true beginning of the floor:— ...”;
PetrieCH7.36:
” The absolute
position, then, of the middle of the S. end of the entrance passage floor will
be, in level,
668.2 – (4140 X sin. 26° 31' 23") – .8 difference of floor offsets = –
1181 ± 1 ?; in distance from N. base of
pyramid
524.1 + 3704.3
= 4228 ± 2? or 306 N. from mid-plane; and in distance E. from the mid–plane
287.0 – [ sin. (3' 55" – 3' 44") x 3704 ] – .4 difference of offsets
= 286.4 ± 1.0.”;
PetrieCH7.64tab:
” Beginning of entrance Vertically Above Pavement
+668.2 ± .1”

See DRAWING SPECIFICATIONS in The
Entrance.
— Petrie’s Plate 9 is corrupted
vertically
[Petrie’s
drawing in Plate.9 shows slightly greater drawn quantities, and growing with
height, than Petrie’s actually down written numerical values],
but perfect horizontally. For us to
take advantage of the exact Petrie values vertically too, a minor adjustment — adopted
to the Petrie given floor value 668.2’’ of the 19th course — has been made,
along with a corresponding more simple clean redrawing, so that we can follow
the fine quality overall in Petrie’s presentation from 1883.
— Calling
ATLANTIS .. ello .. ello .. 111 .. 333

— Roger .. Roger .. Mayday .. Mayday ..
TNED
ACCESSORIES — CheopsAtlasTNED
TNED REFERENCES
THE BREAKTHROUGHS IN TNED
(See also the [excellent (Swedish
edition only)] compilation in [The Breakthroughs in TNED] Genombrotten i TNED).
bNOM:
PetrieCR¦b58 ¦ bOFFSET
The Nominal Cheops Pyramid
CHEOPS RECTANGLE ½ Base
The
two pyramid
agents rJCR¦b16 and
Petrie CR¦b58 cooperate in defining the actual quantitative constants by
which the corresponding Petrie measured quantities have shown to be exposed,
revealed and proved genuine through Petrie’s given measuring tolerances.
In
terming a NOMINAL reference to the corresponding Cheops Pyramid Petrie measured
device, the PetrieCR(CheopsRectangle) agent is defined as exactly
b
= 4534.20’’ = 58R√16000 =
4534.1965 76.. ’’ correspondingly Petrie standard rounded as
b = 4534.20’’ = PetrieCR¦b58
within
Petrie’s given half pyramid base
b
= 4534.40’’ with tolerance ± 0.25’’ as quoted; lowest 4534.15’’.
—
See also the reckoning sets from Background the beginning;
•
(rJ/100R)² = 16
000 ................. precisely:
entire Cheops Pyramid construct
•
100b/rJ = 58
.......................... precisely: entire
Cheops Pyramid construct
•
rJ =
100R√16 000
=
7817.580303’’
=
198.5665397 M
PetrieCR¦b58
•
b =
58rJ/100 = 58R√16 000
=
4534.196 576’’ ................ ; PETRIEb lowest = 4534.15’’ : OK 4534.19’’
=
115.168593 M
See also rJ-CONSTANTS
WITH CONNECTIONS, unless already familiar.
INVESTIGATING EXAMPLES
»NOMINALS
DO NOT MATCH» — The DO. But they don’t.
EXAMPLE 1
PETRIE
GIVEN »VALUES WITH INTERNAL AFFAIRS» — The PetrieCH7.36 described (P°Angle) as quoted ”26° 31’ 23’’ ± 5’’ ?”
INVESTIGATING EXAMPLE — Petrie’s Casing Connected Data (17Feb2020)
»Nominals
don’t match» — Well .. They DO. But they
don’t.
yLeftPart:
with a constant x=4228; xRightPart: with a constant y=1181:
Example
shows: Petrie’s own given nominal
values does NOT justify a relevant connection to the figures specified as
nominal by Petrie himself.
Why is that?
1. The
remnants of the edifice are not quite sufficient to reflect the original —
casing measures are at best close to the original.
2. The
measured parts of the construct are — says the rJCIRCLE complex — realized from a construction plan NOT equal to the actual
visible constructed parts: we must know the plan to understand the decisive
measuring points.
— PetrieCH7.36e
specifies the nominal sloping angle value for the entire descending tunnel (105
M) as ”26° 31’ 23’’ ± 5’’ ?”.
— But
taking the Petrie given nominal xy point values, gives a corresponding 26° 31’
52’’. That is clearly out of the specified picture. So: how is it?
Trying to investigate Petrie’s values in ”Precise Mode” on purpose of
»Enhancing the Precision Insight» of The Mysterious Temple of Cheops Pyramid,
leads us into trouble:
— SOME PARTS OF The figures don’t match, they skew, suggesting ”overflow”,
pointing ”all over the place”, even (far) aside from Petrie’s own specified
tolerances (InEx1).
Divergent information.
— Taking our stand from the rJCIRCLE complex instructions
— we calculate Petrie’s reported measuring values from a known
construction plan
— leads us to the opposite camp:
Convergent information.
— We see that our rJ calculated results end up within the Petrie given
tolerances. Or, if they shouldn’t:: not at all. Burn this. No single rJ calculated
value is allowed to differ from the Petrie given figures and their tolerances —
with Petrie’s given question marks included, if some doubt exists.
Then everything makes sense.
In absolute figures — just (InEx1) to prove these
claims:
rJcalc: P°angle = ArcTan½ — ArcTan(π/[A→G = (xG—xA)√1.25]) =
26° 31'
17.486086'' := 26° 31' 18’’:
— 17.48 rounded is 17.5. With Petrie’s question mark rounded to whole
arc seconds: 18.
Exactly at the lower Petrie
given tolerance border.
The Plan — says The rJCIRCLE.
It also connects to, and
defines Petrie’s 19th floor by the adopted π-triangle’s nValue :
nValue = π/√1.25 =
2.809925892 :
nValue + xA = 668.1482038706’’ versus the PetrieCH7.35¦64tab 668.2 ±
0.1. Approved.
√1.25 :
— This figure connects to the ArcTan½ line and its PREFIXxSIN sine square —
inverted as 1/0.8² = 1.25.
CheopsATLAS —
Feb2020
innehåll: content SÖK
på denna sida Ctrl+F · sök alla ämnesord överallt i SAKREGISTER · förteckning över alla
webbsidor
Universums Historia —
CheopsATLAS in UNIVERSE HISTORY
ämnesrubriker
innehåll —
CONTENT
Type18 — 60 ·
18 = 1080: QUEEN ceiling
R — THE GOLDEN
SECTION CONSTANT
TCAF— The Cheops Atlas Foundation
Continued NatCH intro Description
FIRST »SIMPLE» OBSERVATION 
First most simple and direct
observation
TheGalleryTES—THE
GALLERY TOP END SLOPE
yPGcalcrJ —
THE yPG GALLERY POINT CALCULATION
TGScol — Collected Petrie data on TGS
PHASE1table
— TABLE OF RESULTS Jan2020 — THE 7 FOUNDATION POINTS — K L M G H B A
GSTarCO — THE
7 FOUNDATION POINTS
TarcCO — The ArcTan½ line 7 point coordinates
EnterGSPyramid
— The GS-paragon Pyramid Entrance
ConPent—HOW PETRIE RECKONED THE Pyramid ENTRANCE GEOMETRY
PHASE2 — The B-POINT
ConMes — The construct and The measure
CoctB —
TheConstruct@B
CoctBme —
TheMeasuredConstruct@B
MisPI — MISSING
PETRIE INFORMATION? — No. But a small clarification was needed.
ExCon —The
Construct — in detail
SIO—SecureInspectionOffset
PHASE2sec—The Petrie B-POINT
TeSeal—HOW THE CONSTRUCT BECOMES »SEALED»
TransEqui—Transposition
Equivalent
TP1PlanCon—The
PUSH-contracted parts: PLAN and Construct
TVTuS—TheVerticalTunnelSum
Petrie19thProof—Proving
the Petrie 19th floor arithmetics
PBP—PlugBlockPart
PCH739ref—quote
PetrieCH7.39
dpLoHiMen—DESCENDING PASSAGE LowHighMEAN:
WholeRmult—Whole number R-multiples
KingsMid—King’s
Chamber midpoint
QueenSir—Queen’s
Series
QueenFIn—QueenFloorIn
MiUNITcomparing—ExactComparingBasics,
the MiUNIT
k0—SPECIFIC CHEOPS RECTANGLE RELATION
LIC—THE LINE
INTERSECTING CONNECTION
ArcTan05GS—THE ArcTan½ LINE IN THE GS BODY
SourcesGal—End GALLERY SOURCES
PCH6s24—quote PetrieCH6.24: PYRAMID STAIRCASE MASONRY SLOPING ANGLE
PCH6s25—quote
PetrieCH6.25
PCH6s29—quote
PetrieCH6.29
PCH6s23—quote
PetrieCH6.23
PCH631ref—quote
PetrieCH6.31
PetrieSignal—quote PetrieCH7.39
PetrieSignal1546—quote PetrieCH7.45
PetrieSignal2621—quote PetrieCH7.38
PCH746ref—quote PetrieCH7.46
PCH7s35—quote
PetrieCH7.35¦36¦64tab
bNOM —The Nominal
Cheops Pyramid CHEOPS RECTANGLE ½ Base
InvEx—INVESTIGATING
EXAMPLES
referenser
[HOP]. HANDBOOK OF PHYSICS, E. U. Condon, McGraw-Hill 1967
Atomviktstabellen
i HOP allmän referens i denna presentation, Table 2.1 s9–65—9–86.
mn =
1,0086652u ...................... neutronmassan
i atomära massenheter (u) [HOP Table 2.1 s9–65]
me =
0,000548598u .................. elektronmassan
i atomära massenheter (u) [HOP Table 10.3
s7–155 för me , Table 1.4 s7–27 för u]
u = 1,66043 t27 KG .............. atomära massenheten [HOP Table 1.4 s7–27,
1967]
u = 1,66033
t27 KG .............. atomära massenheten [ENCARTA 99 Molecular
Weight]
u = 1,66041 t27 KG
............... atomära massenheten
[FOCUS MATERIEN 1975 s124sp1mn]
u = 1,66053886 t27 KG ........ atomära
massenheten [teknisk kalkylator, lista med konstanter SHARP EL-506W
(2005)]
u = 1,6605402 t27 KG .......... atomära
massenheten [@INTERNET (2007) sv. Wikipedia]
u = 1,660538782 t27
KG ...... atomära massenheten [från www.sizes.com],
CODATA
rekommendation från 2006 med toleransen ±0,000 000 083 t27 KG (Committe
on Data for Science and Technology)]
c0 = 2,99792458 T8 M/S ........ ljushastigheten
i vakuum [ENCARTA 99 Light, Velocity, (uppmättes i början på
1970-talet)]
h = 6,62559 t34 JS ................. Plancks konstant [HOP s7–155]
— Det internationella standardverket om universum sammanställt vid universitetet i Cambridge, The Cambridge Encyclopaedia of Astronomy, London 1977.
[BKL]. BONNIERS KONVERSATIONS LEXIKON, 12 band A(1922)-Ö(1928) med SUPPLEMENT A-Ö(1929)
t för 10–, T för 10+,
förenklade exponentbeteckningar — simplified notations: t for TEN
RAISED TO minus and T for TEN RAISED TO plus.
MAC, här ofta använd
förkortning för Modern ACademy — etablerad
vetenskap sedan början av 1800-talet
TNED — Related PHYSICS And MATHEMATICS —
Se särskild djupbeskrivning av innebörden i begreppet relaterad framställning.
(Toroid Nuclear Electromechanical Dynamics), eller Toroidnukleära Elektromekaniska
Dynamiken är den dynamiskt ekvivalenta resultatbeskrivning som
följer av härledningarna i Planckringen
h=mnc0rn, analogt Atomkärnans
Härledning. Beskrivningen enligt TNED är relaterad,
vilket innebär: alla, samtliga, detaljer gör anspråk på att vara fullständigt
logiskt förklarbara och begripliga, eller så inte alls. Med TNED förstås
(således) också
RELATERAD FYSIK OCH
MATEMATIK. Se även uppkomsten av termen TNED i Atomkärnans Härledning.
See
also TNED FROM THE BEGINNING (Swedish
edition only Aug2019).
SHORT ENGLISH — TNED in general is not found @INTERNET except under
this domain
(Universe[s]History, introduced @INTERNET 2008VII3).
TNED or Toroid Nuclear Electromechanical Dynamics is
the dynamically equivalent resulting description following the deductions in THE PLANCK
RING, analogous AtomNucleus’ Deduction. The
description according to TNED is related, meaning: all, each, details
claim to be fully logically explainable and understandable, or not at all. With
TNED is (hence) also understood RELATED PHYSICS AND MATHEMATICS. See also the
emergence of the term TNED
in AtomNucleus’ Deduction.
Senast uppdaterade version: 2024-03-01
*END.
Stavningskontrollerat 2020-03-26¦26Mar2020.
rester
*
åter till portalsidan · portalsidan är www.UniversumsHistoria.se
≈
Δ Ĵ ∫ α √ π → ∞ τ π ħ
ε UNICODE — often used charcters in mathematical-technical-scientifical
descriptions
σ
ρ ν ν π τ γ λ η ≠ √ ħ
ω → ∞ ≡ ↔↕ ħ ℓ
Ω
Φ ϕ ϕ
Ψ Σ Π Ξ Λ Θ Δ ~
α
β γ δ ε λ θ κ π ρ τ φ
σ ω ∏ √ ∑ ∂ ∆ ∫ ≤ ≈
≥ ← ↑ → ∞ ↓
ζ
ξ
Arrow symbols, direct via
Alt+NumPadKeyboard: Alt+24 ↑; 25
↓; 26 →; 27 ←; 22 ▬
23
↨ — also 18 ↕; 29 ↔
åter till portalsidan · portalsidan är www.UniversumsHistoria.se